
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа № 1. Моделирование в пространстве состояний одноконтурной системы управления.Содержание книги
Поиск на нашем сайте
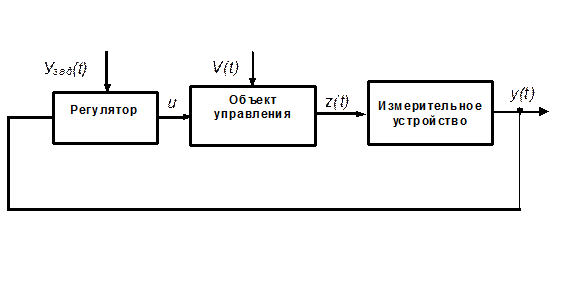
Тема лабораторной работы. Моделирование в пространстве состояний одноконтурной системы управления. Цель работы. Получение практических навыков составления математической модели в пространстве состояний одноконтурной системы управления и моделирования переходного процесса системы управления на ЭВМ в среде Mathcad. Задание. Функциональная схема системы изображена на рисунке 1. Структурные схемы регулятора и измерительного устройства приведены на рисунках 2 и 3.
Рис. 1. Функциональная схема системы управления
П-регулятор имеет передаточную функцию
где:
Рис. 2. Структурная схема регулятора
Объект управления имеет передаточную функцию по управляющему воздействию
и передаточную функцию по возмущающему воздействию
Измерительное устройство имеет передаточную функцию:
Рис. 3. Структурная схема измерительного устройства Параметры уравнений (1)-(3) для различных вариантов задания приведены в таблице1.
При выполнении лабораторной работы необходимо: 1. Составить математическую модель в пространстве состояний объекта управления; 2. Составить математическую модель в пространстве состояний регулятора; 3. Составить математическую модель в пространстве состояний измерительного устройства; 4. Составить математическую модель в пространстве состояний системы управления; 5. Составить разностную модель системы управления. Шаг квантования времени принять равным 6. Моделированием на ЭВМ построить графики переходных процессов для переменных состояния При моделировании считать, что требуемый закон изменения управляемой переменной задан уравнением:
Погрешность измерений формировать с помощью генератора случайных чисел по алгоритму:
7. Составить отчет.
Методические указания к выполнению задания
1. Определение уравнений состояния по заданной передаточной функции системы. Математическую модель в пространстве состояний объекта управления следует представить в следующем каноническом виде:
где: Задача определения уравнений состояния по передаточной функции системы есть, по существу, известная в теории дифференциальных уравнений задача приведения линейных уравнений n -го порядка к нормальной форме Коши. Некоторое отличие состоит в том, что в теории управления принято рассматривать уравнения, в которые входят производные не только от выхода, но и от входа системы. Полагаем, что система задана передаточной функцией (с параметром
и является строго реализуемой, т.е. r < n. Из передаточных функций (2) и (3) видно, что объект управления имеет 2 переменные состояния: Уравнения состояния, получаемые по заданной передаточной функции системы, определяются с точностью до произвольного невырожденного преобразования. Поэтому данной передаточной функции соответствует множество различных уравнений состояния и поставленная задача решается неоднозначно. Выбор формы уравнений состояния зависит от того, как они будут использоваться в дальнейшем. Рассмотрим некоторые возможные варианты. В некоторых приложениях желательно, чтобы значения переменных состояния соответствовали определенным физическим переменным. Тогда структура матриц А, В, G и С в уравнениях (7) и (8) оказывается заданной и задача состоит в нахождении некоторых их элементов. Эта задача может быть решена на основе обратного перехода от уравнений состояния к передаточной функции методом неопределенных коэффициентов. Далее рассмотрим ситуацию, в которой физический смысл переменных состояния не имеет значения и выбор вида уравнений состояния происходит из других соображений. Прежде всего, если задана только передаточная функция, естественно искать ее минимальную реализацию, т.е. такую форму уравнений состояния, при которой заданная передаточная функция получается при наименьшей размерности вектора переменных состояния(следовательно, - при минимально возможном порядке уравнений (7) и (8)). Как известно, минимальная реализация соответствует невырожденным (полностью управляемым и полностью наблюдаемым) системам. Для систем с одним входом и одним выходом это эквивалентно тому, что по уравнениям состояния получается несократимая передаточная функция, степень полинома знаменателя которой совпадает с размерностью вектора состояния. Поэтому в дальнейшем будем считать, что в числителе и знаменателе заданной передаточной функции отсутствуют явно (структурно) выраженные общие сомножители. Это условие, впрочем, не исключает того, что передаточная функция задана в общем виде, но при определенных сочетаниях параметров найденная реализация не будет минимальной. Итак, считаем, что степень знаменателя передаточной функции задана и равна n. Поскольку характеристический многочлен матрицы A совпадает со знаменателем передаточной функции, а степень характеристического многочлена равна размерности вектора переменных состояния, то искомые уравнения состояния должны быть n -го порядка. Теперь можно использовать одну из канонических форм. Проще всего получаются уравнения состояния в форме управляемого канонического представления (УКП). Эти уравнения для передаточной функции (9) составляют по следующему алгоритму:
....
Для представления полученных уравнений в матричной форме (7), (8) необходимо задать матицы A, B и C следующим образом:
Действуя аналогичным образом с передаточной функцией (8) получим матрицу 2. Составление уравнений состояния измерительного устройства. Из структурной схемы измерительного устройства (рис. 3) следует, что выходной сигнал
3. Определение уравнений состояния П-регулятора. Из структурной схемы регулятора (рис. 2) и уравнений (1), (8) следует, что его выходной сигнал
4. Составление уравнений состояния замкнутой системы управления. Для этого из уравнения состояния объекта управления необходимо исключить управляющее воздействие, используя уравнение (14). В результате получим модель системы управления в пространстве состояний в следующем виде:
где:
Уравнения (15)-(17) описывают модель системы управления в пространстве состояний и их можно использовать для анализа системы управления и моделирования переходных процессов в этой системе. 6. Составим дискретную модель системы управления методом Эйлера. Для этого выполним квантование времени с постоянным шагом
В дискретный момент времени
В правых частях дифференциальных уравнений в дискретный момент времени
В результате получим следующую систему разностных уравнений:
Для построения графиков переходных процессов необходимо решить на ЭВМ систему уравнений (15), (16) (с использованием формул (a), (b), (c)) с помощью математического пакета Mathcad. Построить графики переходных процессов для переменных состояния объекта управления 7. Составить отчет по результатам выполнения задания (пояснения к п.п. 1-7 методических указаний).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 103; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.16.251 (0.007 с.) |

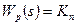 и, поэтому, формирует управляющее воздействие
и, поэтому, формирует управляющее воздействие 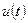 по алгоритму:
по алгоритму: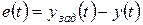 ;
;  , (1)
, (1)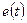 − сигнал рассогласования в момент времени
− сигнал рассогласования в момент времени 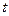 между требуемым значением
между требуемым значением 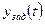 и измеренным значением
и измеренным значением 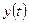 управляемой переменной
управляемой переменной 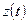 ;
; 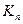 − коэффициент усиления П-регулятора.
− коэффициент усиления П-регулятора.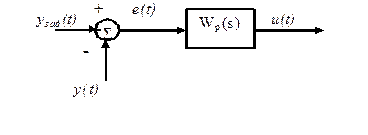
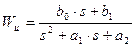 (2)
(2)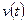 :
: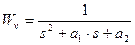 . (3)
. (3)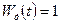 . (4)
. (4)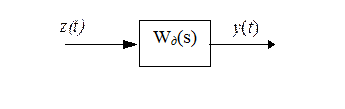
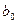
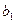
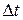 =0,01 с.
=0,01 с.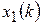 и
и 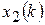 объекта управления (
объекта управления (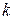 =0, 1, …, N).
=0, 1, …, N).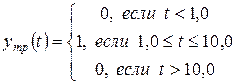 . (5)
. (5)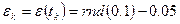 . (6)
. (6)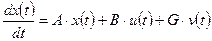 ; (7)
; (7)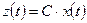 , (8)
, (8)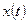 − вектор переменных состояния;
− вектор переменных состояния; 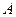 ,
, 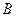 ,
, 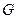 и
и 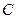 − матрицы, элементы которых следует определить по заданным передаточным функциям элементов системы управления и ее функциональной схеме.
− матрицы, элементы которых следует определить по заданным передаточным функциям элементов системы управления и ее функциональной схеме.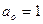 ):
):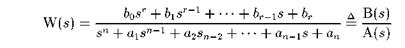
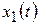 и
и 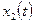 , (следовательно, n=2, а r=1).
, (следовательно, n=2, а r=1).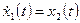 ,
,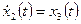 ,
,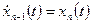 ,
,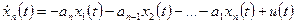 ,
,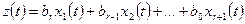 .
.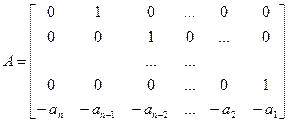 ;
; 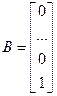 ; (11)
; (11)  .
.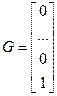 . (12)
. (12)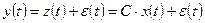 . (13)
. (13)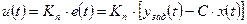 . (14)
. (14)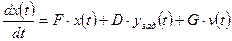 ; (15)
; (15)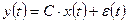 , (16)
, (16)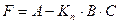 ;
; 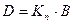 ;
; 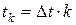 ;
; 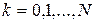 .
.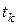 заменим производные по времени приближенными выражениями:
заменим производные по времени приближенными выражениями: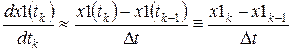 ;
;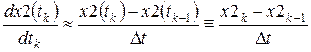 .
.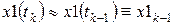 ;
; 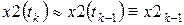 ;
; 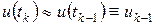 .
.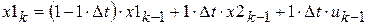 ;
; 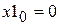 ; (a)
; (a) 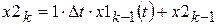 ;
; 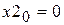 ; (b)
; (b)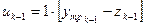 ; k=1, 2, …, N. (c)
; k=1, 2, …, N. (c)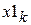 и
и 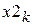 .
.


