
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Строим эпюру продольных сил NСодержание книги
Поиск на нашем сайте
Воспользуемся методом сечений. Делаем по одному сечению в произвольном месте каждого из трех участков стержня. Cечение 1 – 1. Отбросим верхнюю часть стержня (рис. 6.1, б). Само сечение 1 – 1 мысленно считаем неподвижным. Мы видим, что внешняя сила P1 растягивает рассматриваемую нижнюю часть стержня – реакция стержня N1 (внутренняя продольная сила) уравновесит внешнюю силу P1. N1 = P1 = 100 кН. Сечение 2 – 2. Внешняя сила P1 растягивает рассматриваемую нами нижнюю часть стержня, а сила P2 ее сжимает (рис. 6.1, в). В сечении 2 – 2 должна возникнуть внутренняя сила N2, противодействующая сжатию, то есть направленная к сечению. Она равна: N2 = P2 - P1 = 300 – 100 = 200 кН. Сечение 3 – 3. Отбросим теперь часть стержня, расположенную ниже этого сечения. Внутренняя продольная сила N3 должна уравновесить внешнюю (реактивную) сжимающую силу R (рис. 6.1, г). Поэтому она направлена к сечению и равна: N3 = R = 200 кН. Если мы отбросим верхнюю часть стержня, то в этом случае продольная сила N3также противодействует сжатию. Она равна: N3= P2 - P1 = 300 – 100 = 200 кН. Строим по вычисленным значениям эпюру N (рис. 6.1, д). В пределах каждого из участков стержня продольные силы постоянны, то есть эпюра N параллельна оси. «Скачок» имеет место только в местах приложения внешних сил. 3. Строим эпюру нормальных напряжений σ Нормальное напряжение, возникающее в k–м поперечном сечении стержня при растяжении (сжатии), вычисляется по следующей формуле
где N и F– продольная сила и площадь k–го поперечного сечения стержня соответственно. В первом поперечном сечении стержня нормальное напряжение равно
во втором –
в третьем –
Строим по вычисленным значениям эпюру σ (рис. 6.1, е). В пределах каждого из участков стержня напряжения постоянны, то есть эпюра напряжений параллельна оси. На эпюре σ «скачок» имеет место не только в местах приложения внешних сил, но и там, где происходит изменение размеров поперечного сечения стержня. Оцениваем прочность стержня Сопоставляем наибольшее (по модулю) нормальное напряжение σ, которое в нашем примере возникает во втором сечении стержня, с допускаемым напряжением [ σ]. Напомним, что допускаемое напряжение представляет собой долю от предельного напряжения σпр, то есть от напряжения, при котором начинается разрушение материала. Разрушение стали, как пластичного материала, начинается при появлении значительных остаточных деформаций. Поэтому для стали предельное напряжение равно пределу текучести: σпр = σт. Тогда [ σ] = σт/[ n ] = 24/1,5 = 16кН/см2. Условие прочности имеет вид σ max ≤ [ σ] . В нашем случае σ max = 20 кН/см2 > [ σ] = 16 кН/см2, следовательно, прочность стержня на втором участке не обеспечена. Таким образом, площадь поперечного сечения стержня на втором участке необходимо увеличить. Из условия прочности определяем требуемую площадь поперечного сечения стержня на втором участке: F 2 треб ≥ N 2 / [ σ] = 200/16 = 12,5 Принимаем на втором участке F2= 12,5 см2. 5. Вычисляем удлинение всего стержня ∆l При переменных по длине стержня значениях продольной силы и площади поперечного сечения удлинение вычисляется по формуле
где E – модуль Юнга, а l – длина соответствующего участка стержня. Тогда ∆l = 10*100/2*104 – 20*150/2*104 - 10*200/2*104 = - 0,2 см. Таким образом, длина стержня уменьшается на 2 мм. Рис. 6.2. Схемы для решения задач.
Таблица 6.1. Исходные данные к задаче на растяжение и сжатие
ЗАДАНИЕ 7. РАСЧЕТ НА ПРОЧНОСТЬ ПРИ СРЕЗЕ И СМЯТИИ. Элементы, которыми соединяют различные детали, например, заклепки, штифты, болты (без зазора) в основном рассчитывают на срез. Расчет носит приближенный характер и основан на следующих допущениях: 1) в поперечных сечениях рассматриваемых элементов возникает лишь один силовой фактор – поперечная сила Q; 2) при наличии нескольких одинаковых соединительных элементов каждый из них воспринимает одинаковую долю общей нагрузки, передаваемой соединением; 3) касательные напряжения распределены по сечению равномерно. На смятие, как правило, рассчитывают элементы, которые соединены заклепками, штифтами, болтами. Смятию подвергаются стенки отверстий в зонах установки соединительных элементов. Обычно расчет на смятие выполняют для соединений, соединительные элементы которых рассчитывают на срез. При расчете на смятие принимают, что силы взаимодействия между соприкасающимися деталями равномерно распределены по поверхности контакта и в каждой точке нормальны к этой поверхности. Силу взаимодействия, принято называть напряжением смятия. Расчет на прочность выполняется по формуле: σ p = где А – ширина листа, м;
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 130; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.206.229 (0.008 с.) |

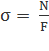 ,
,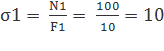 кН/см2,
кН/см2,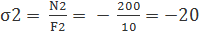 кН/см2,
кН/см2,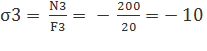 кН/см2.
кН/см2. см2.
см2.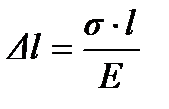

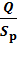 =
= 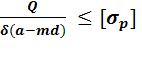 ,
,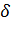 – толшина листа, м;
– толшина листа, м;


