
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гапоу ЛО «борский агропромышленный техникум»Содержание книги
Поиск на нашем сайте
ГАПОУ ЛО «Борский агропромышленный техникум» МЕТОДИЧЕСКИЕ УКАЗАНИЯ И КОНТРОЛЬНЫЕ ЗАДАНИЯ по дисциплине «Техническая механика» для студентов по специальности 35.02.07 «Механизация сельского хозяйства»
Разработал: Филиновский В.Ф.
Бор 2018 СОДЕРЖАНИЕ Пояснительная записка…………………………………………………………….3 Задания на самостоятельную работу……………………………………………...7 Задание 1. Расчет плоской системы сходящихся сил……………………...7 Задание 2. Определение реакций опор двухопорной балки.........................14 Задание 3. Центр тяжести плоской фигуры…………………........................19 Задание 4, 5. Кинематика, динамика…...........................................................23 Задание 6. Расчет на прочность при растяжении и сжатии….......................30 Задание 7. Расчет на прочность при срезе и смятии…...................................36 Задание 8. Расчет прочности балки при изгибе…..........................................43 Задание 9. Кручение стержня круглого сечения….........................................54 Задание10. Расчет привода редуктора…..........................................................60 Список используемых источников………………………………………………65 Дисциплина «Техническая механика» для данной специальности включает в себя три раздела: теоретическую механику, сопротивление материалов и детали машин. В результате освоения дисциплины обучающийся должен уметь: В результате освоения дисциплины студент должен уметь: - читать кинематические схемы; - проводить расчет и проектировать детали и сборочные единицы общего назначения; - проводить сборочно – разборочные работы в соответствии с характером - определять напряжение в конструкционных элементах; - производить расчеты элементов конструкций на прочность, жесткость и устойчивость; - определять передаточное отношение. В результате освоения дисциплины студент должен знать: - виды машин и механизмов, принципы действия, кинематические и динамические характеристики; - типы соединения деталей и машин; - основные сборочные единицы и детали; - характер соединения деталей и сборочных единиц; - принцип взаимозаменяемости; - виды движений и преобразующие движения механизмы; - виды передач, их устройство, назначение, преимущество и недостатки, условные обозначения на схемах; - передаточное отношение и число; - методику расчета элементов конструкций на прочность, жесткость и устойчивость при различных видах деформации. Предлагаемое учебное пособие подготовлено в соответствии с государственным стандартом по этой дисциплине. Предназначаемые студентам методические рекомендации дают возможность целенаправленно ориентировать их в основных вопросах программы. В методических рекомендациях указана основная литература. При написании домашней самостоятельной работы студенты могут использовать предлагаемую литературу, а также использовать другую литературу по дисциплине. В процессе изучения курса студенту необходимо выполнить домашнюю самостоятельную работу. Выполнение данной работы определяется степень усвоения студентами изученного материала и умение применять полученные знания при решении практических задач. Каждый студент должен выполнить 10 заданий различного уровня сложности. В каждом задании по 10 вариантов (25 в заданиях 1, 10). Вариант контрольной работы определяется по последним цифрам списочного состава студентов в группе (согласно таблице 1). Например, для студента, имеющего номер в списке 1, 11, 21 номер задания 1, а для студента, имеющего номер в списке 10, 20, 30 номер задания 10. При выполнении домашней самостоятельной работы студент должен соблюдать следующие требования: 1. К выполнению самостоятельной работы следует приступать лишь после того, как весь учебный материал задания будет тщательно и глубоко изучен; 2. Самостоятельная работа должна представляться в сроки указанные в учебном графике; 3. Работа должна быть выполнена аккуратно, разборчивым почерком; 4. В самостоятельную работу записывается условия задач; 5. Решение задач следует сопровождать пояснениями; 6. Вычислениям должны предшествовать исходные формулы; 7. Для всех исходных и вычислительных физических величин должны указываться размерности; 8. Приводятся необходимые эскизы, схемы; 9. На каждой странице оставляются поля шириной 3 – 4 см, для замечаний проверяющего работу; 10. Зачтенная самостоятельная работа предъявляется преподавателю на экзамене; 11. Самостоятельная работа не принимается на рецензию и возвращается студенту с указанием причин в следующих случаях: a. если студент выполнил не свой вариант самостоятельной работы; b. если работа выполнена небрежно, неразборчивым почерком; c. если самостоятельная работа выполнена не в полном объеме. В методических указаниях приведены примеры решения и оформления задач.
Решение задач рекомендуется производить по правилам: 1. Перед решением задачи необходимо переписать полностью ее условие с числовыми данными, составить эскиз в масштабе и указать на нем в числах все величины, необходимые для дальнейшего расчета, 2. Решение задач дополняйте краткими пояснениями и чертежами, на которых визуализированы входящие в расчет величины, 3. Перед использованием формулы для определения напряженно-деформированного состояния необходимо изучить соответствующую тему лекций по сопромату, чтобы понять физический смысл всех величин, входящих в нее, 4. При подстановке в используемую формулу величин силы, момента или длины необходимо перевести их в одну систему единиц, 5. При решении задач точность расчетов не должна превышать трех значащих цифр (результат решения задачи не может быть точнее заложенных в расчетные формулы предпосылок), 6. Заканчивать расчеты нужно анализом результатов. Анализ результатов решения поможет избежать нелепых ошибок и оперативно их устранить. 7. В различных учебниках и задачниках могут отличаться обозначения величин: например, площадь – S, F, A; сила – P, F. Задание 1 выполняется после изучения тем: Основные понятия и аксиомы статики, Плоская и пространственная система сходящихся сил. Основной источник – Вереина Л.И. Техническая механика: учебник для сред. проф. образования / Л.И. Вереина, М.М. Краснов. – 5-е изд., испр. И доп. – М.: Издательский центр «Академия», 2014. – 352 с. Задание 2 выполняется после изучения темы: Плоская и пространственная система сил. Задания 3 выполняется после изучения темы: Центр тяжести тел. Задание 4 и 5 выполняется после изучения темы: Кинематика и динамика. Задание 6 выполняется после изучения темы: Растяжение и сжатие тел. Задание 7 выполняется после изучения темы: Срез и смятие. Задание 8 выполняется после изучения темы: Изгиб. Задание 9 выполняется после изучения темы: Кручение. Задание 10 выполняется после изучения темы: Детали машин. ЗАДАНИЯ НА САМОСТОЯТЕЛЬНУЮ РАБОТУ ЗАДАНИЕ 1. РАСЧЕТ ПЛОСКОЙ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ Порядок решение задач При решении задач на равновесие системы сходящихся сил можно использовать три метода: графический, графо-аналитический и аналитический (метод проекций). Необходимо учитывать, что если рассматривается равновесие плоской системы сходящихся сил, приложенных к одному телу, число неизвестных величин не должно превышать двух (условие статической определимости задачи с плоской системой сходящихся сил): При графическом методе решения во всех четырех случаях можно построить замкнутый силовой многоугольник и найти в нем неизвестные величины. Графо-аналитический метод целесообразно применять в тех случаях, когда рассматривается равновесие трех сил. При этом по условию задачи в произвольном масштабе строится замкнутый треугольник, который затем решается на основе геометрических либо тригонометрических соотношений. Метод проекций целесообразно применять для решения задач с числом сил больше трех. Для решения задач статики можно воспользоваться следующим планом. 1. Выбрать объект, равновесие которого следует рассмотреть. Таким объектом может быть точка, тело либо система тел. 2. Приложить действующие на этот объект силы. 3. Отбросить связи, заменив их действие реакциями. 4. Определить тип полученной системы сил. Убедиться, что число неизвестных в задаче равно числу уравнений равновесия, то есть выяснить статическую определимость задачи. 5. Выбрать оси координат. При выборе осей следует помнить, что уравнение будет проще, если в него входит меньшее количество неизвестных, то есть необходимо, по возможности, оси координат брать перпендикулярно одной из неизвестных реакций. 6. На основе полученной схемы сил построить замкнутый силовой треугольник (если рассматривается равновесие трех сил) или составить уравнения равновесия; причем при составлении уравнений проекций оси целесообразно расположить так, чтобы их направления были параллельны или перпендикулярны к искомым силам (оси проекций также показываются на рисунке); 7. После решения уравнений равновесия полученные результаты необходимо проверить либо при помощи неиспользованных уравнений или соотношений, либо путем решения задачи другим способом. Пример 1. (рис.1.1) Два стержня связаны между собой и со стеной шарнирами. К шарниру В на нити подвешен груз весом 100 Н. Определить усилия в стержнях.
Связями для точки В служат стержни АВ и ВС. Отбрасывая связи заменим их реакциями – S1 и S2, которые направлены вдоль стержня. Направляя усилия в от точки В предполагаем, что оба стержня растянуты. На точку В действуют три силы, лежащие в одной плоскости и пересекающиеся в одной точке, то есть плоская сходящаяся система сил, для которой можно составить два уравнения равновесия: S F кx=0, S Fкy=0. В этих уравнениях находится 2 неизвестных - усилия S1 и S2. Оси координат направим вдоль стержней. Составляем уравнения равновесия. S F kx= S1 - P cos(600) = 0; (1) S F ky= S2 +P cos(300) =0. (2) Из первого уравнения находим: S1 = P cos(600) = 100 *0,5 = 50 H, из второго: S2 = - P cos(300) = -100* 0,867= - 86,7 H. Усилие S2 получилось отрицательным, то есть стержень ВС будет не растягиваться, а сжиматься.
S1 = P cos(600) = 100 *0,5 = 50 H, S2 = P cos(300) = 100* 0,867= 86,7 H. По теореме синусов:
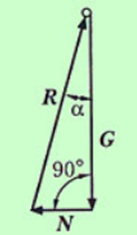
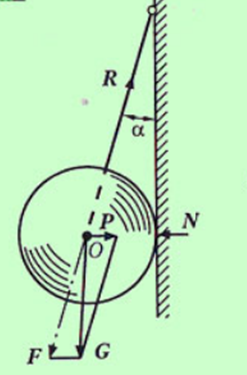
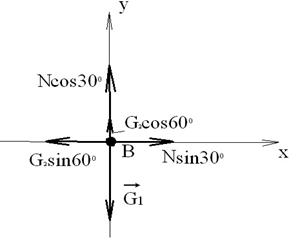
Пример 2. Определить напряжение веревки F и силу давления шара Р на стену, если сила тяжести шара равна G (рис.1.3).
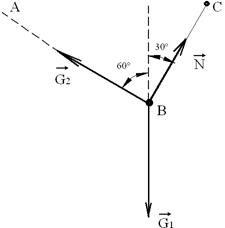
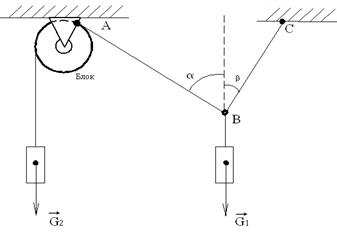
Рис.1.3 Рис.1.4 Решение: Рассмотрим условие равновесия шара. Применив принцип освобождаемости, отбросим связи и заменим их реакциями. Реакция гладкой стены N перпендикулярна стене и проходит через центр шара. Реакция веревки F направлена вдоль линии натяжения веревки и тоже проходит через центр шара. Применим к системе сил условие равновесия S F I = 0 или G + N + R =0. Строим замкнутый силовой треугольник в произвольном масштабе вектора известной силы G (рис.1.4). Направление обхода треугольника (т.е. направление стрелок) определяется направлением этой силы. Из построенного силового треугольника получим соотношения: N = G*tgα, R = G/cosα. Искомая сила Р давления шара на стену равна, согласно аксиоме взаимодействия, по модулю реакции N стены, но направлена в противоположную сторону. Натяжение веревки F равно по модулю ее реакции R. Эту задачу можно решить, разложив силу тяжести шара G по реальным направлениям (направлениям реакций) на составляющие - сила давления шара на стену Р и натяжение веревки F, причем согласно аксиоме взаимодействия: F = R, Р = N. Из построенного параллелограмма (рис.1.3) легко определить искомые величины. Такой метод решения называют методом разложения силы. Пример 3. Два груза весом G1 и G2 находятся в равновесии (рис.1.5). Определить N - натяжение веревки ВС и вес G1, если G2 = 50H; угол α = 600, β =300. Решение Т. к. связь (веревка) – гибкая, следовательно, на участке АВ веревка растянута усилием G2. Перенесем в точку В вес G1 и усилие G2 по направлению ВА (т. е заменим действие связи вектором реакции G2. Получим систему сходящихся сил; значит реакция N пройдет также через т. В.
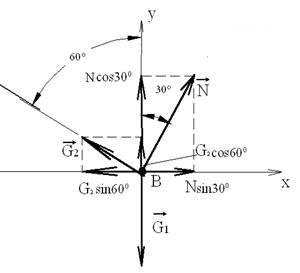
Рис. 1.5 Рис. 1.6 Изобразим систему сил (рис. 1.6), где направления G2 и N показывают, что обе веревки растянуты. Далее обозначим систему координат хВy и спроектируем все действующие силы на оси х и y ( рис.1.7 ): S F ix = 0; -G2 sin600 + Nsin300 = 0 (1) S F iy = 0; -G1 + G2 соs600 + Nсоs300 = 0 (2)
Рис.1.7
Из (1): N = G2
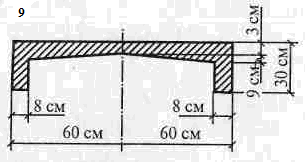
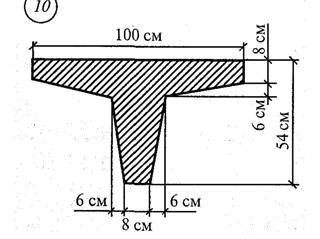
Пример решения задач Определить положение центра тяжести в сечении, состоящего из простых геометрических фигур.
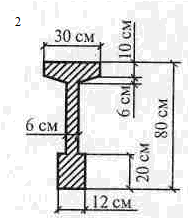
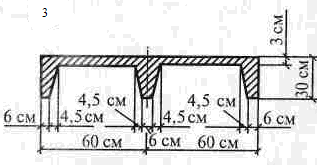
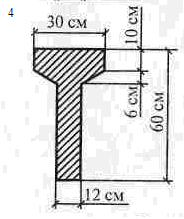
Решение 1. Разбиваем сечение на три части (рис.3.1): 1 – прямоугольник; 2 – трапеция; 3 – прямоугольник. 2. Отмечаем центры тяжести каждой отдельной части. Проводим оси координат. 3.Определяем координаты центра тяжести сечения С (хС, уС). составное сечение симметрично, поэтому центр тяжести находится на оси симметрии и координата хС = 0, то есть С (0, уС).
- вычисляем площадь отдельных фигур
- определяем координаты центров тяжести отдельных фигур:
Данные можно занести в таблицу.
Таблица 3.3. Схемы задач.
ЗАДАНИЯ 4 и 5. КИНЕМАТИКА И ДИНАМИКА Таблица 4.1. Основные формулы кинематики
Таблица 4.2. Формулы динамики
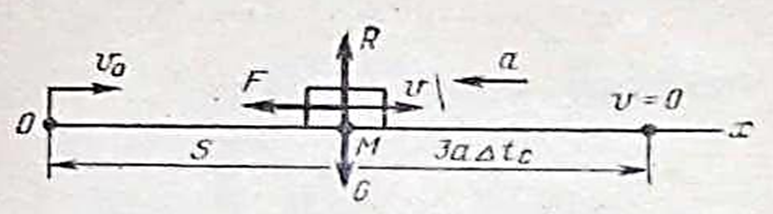
Пример 1. Точка движется прямолинейно по закону S = t4 + 2t, (S – в метрах, t – в секундах). Найти ее среднее ускорение в промежутке между моментами t1 = 2 с, t2 = 4 с, а также истинное ускорение в момент t3 = 3 с. Решение: Определить скорость точки (производная от перемещения) V = dS/dt = 4t3 + 2. Подставив вместо t его значения t1 = 2 с, t2 = 4 с, найдем V1 = 4*23 + 2 = 34 м/с, V2 = 4*43 + 2 = 258 м/с. Следовательно, прирост скорости за данный промежуток времени ∆t = t2 – t1 = 4 – 2 = 2 c. ∆V = V2 – V1 = 258 – 34 = 224 м/с. Среднее ускорение точки аср = ∆V/∆t = 224/2 = 112 м/с2. Для определения ускорения точки в любой момент возьмем производную от скорости по времени а = dV/dt = 12t2. Подставим в это уравнение вместо t его значение t3 = 3 с. а = 12*32 = 108 м/с2. Ответ: аср = 112 м/с2, а = 108 м/с2. Пример 2. Маховик диаметром 0,8 м начинает вращаться из состояния покоя. Через 10 с после начала движения скорость точек обода маховика достигает 8 м/с. Определить ускорение этих точек. Чему равно число оборотов маховика за первые 10 с после начала равнопеременного вращения? Решение: По значению скорости точки находим угловую скорость вращения маховика через 10 с после начала вращения: ɷ = V/r = 8/0,4 = 20 рад/с. Угол поворота маховика за 10 с φ = (ɷ + ɷ 0)*t/2 = (20 + 0)*10/2 = 100 рад. Число оборотов маховика за 10 с Nоб = φ/2π = 100/2*3,14 = 16. Угловое ускорение маховика ε = ɷ/t = 20/10 = 2 рад/с. Нормальное ускорение точек обода маховика в момент t = 10 с. аn = ɷ2*r = 202*0,4 = 160 м/с2. Касательное ускорение точек обода маховика аτ = ε* r = 2*0,4 = 0,8 м/с2. Ответ: Nоб = 16, ε = 2 рад/с, аn = 160 м/с2, аτ = 0,8 м/с2. Пример 3. Для остановки поезда, движущегося по прямолинейному участку пути со скоростью V = 10 м/с, производится торможение. Через сколько секунд остановится поезд, если при торможении развивается постоянная сила сопротивления, равная 0,02 силы тяжести поезда. Какой путь пройдет поезд до остановки? Решение: Поезд совершает поступательное движение. Рассматривая его как материальную точку М (рис.), движущуюся в направлении оси Ох, укажем действующие силы: G – сила тяжести поезда, R - нормальная реакция рельсов, F - сила сопротивления, направленная противоположно вектору скорости. Силы G, R уравновешиваются согласно аксиоме действия и противодействия.
Рис. 4.1. Схема задачи. По теореме об изменении количества движения материальной точки в проекциях на ось Ох m*V – m*V0 = - F*∆t, Так как F = 0,02* G = 0,02*m*g, t0 =0, V0 = 10 м/с, V = 0, получим - m*V0 = - 0,02 m*g*∆t. Откуда ∆t = V0/0,02*g = 10/0,02*9,8 = 51 с. Для определения пройденного пути поездом до его остановки воспользуемся теоремой об изменении кинетической энергии m*V2/2 - m*V02/2 = F*S*cosα. Работа силы торможения отрицательна (α = 1800) и cosα = -1, поэтому - m*V02/2 = - 0,02* m*g*S, Путь, пройденный поездом S = V02/(2*0,02*g) = 102/(2*0,02*9,8) = 225 м. Ответ: S = 225 м. Таблица 3.3. Задания для решения.
1. По дуге радиусом r = 1200 м движется поезд, его скорость в начале движения по дуге составляет V0=60 км/ч (16,7 м/с). После того, как поезд прошел расстояние 800 м, его скорость уменьшилась до 36 км/ч (10 м/с). Определить полное ускорение в начале и конце движения. 2. Прямолинейное движение точки описывается уравнением S = 20 + 5t + 2t2. Определить расстояние от начала отсчета через 10 секунд, начальную, конечную скорость и ускорение точки. 3. Определить радиус кривизны выпуклого моста в верхней точке, если сила давления автомобиля при его движении по мосту с постоянной скоростью 72 км/ч составляет 10 кН. Масса автомобиля 1200 кг. 4. Тело массой 5 кг падает с высоты 80 м. Определить время падения t и скорость v в момент достижения Земли, работу силы тяжести.. 5. Тело под действием горизонтальной силы F = 80 H движется прямолинейно по горизонтальной гладкой поверхности (без трения). Уравнение движения имеет вид: S = 4t + 2t2, где S – в метрах, t – в секундах. Определить массу этого тела, пройденное расстояние за 10 с. 6. Тело массой 2 кг брошено вертикально вверх с начальной скоростью 20 м/с. Определить высоту и время подъема тела, изменение количества движения. 7. При отходе от станции поезд через 5 мин набрал скорость 72 км/ч. Определить ускорение, пройденный путь за это время, работу, выполненную поездом, если его масса 500 т. 8. Вагонетка с грузом массой 500 кг начинает двигаться из состояния покоя равноускоренно по горизонтальному пути и через 10 с достигает скорости v1 = 2 м/с. Определить силу, движущую вагонетку, если сопротивление движению составляет 0,02 веса вагонетки. 9. Автомобиль массой 1800 кг движется по выпуклому мосту с постоянной скоростью 72 км/ч. Определить максимальную силу давления на мост, если радиус кривизны его 180 м. 10. Найти величину угловой скорости ω и величину линейной скорости v искусственного спутника Земли, если известно, что он вращается по круговой орбите с периодом обращения Т = 88 мин, и его орбита расположена на расстоянии h = 200 км от поверхности Земли. 11. Шкив диаметром D = 500 мм передает мощность Р =8 кВт при частоте вращения n = 600 мин-1. Определить вращающий момент M и окружную силу F. 12. Ручной подъемный механизм имеет рукоятку длиной L = 500 мм. Рабочий, прикладывая к ее концу силу F = 200 Н, вращает ее с угловой скоростью ɷ = 20 рад/с. Определить работу, затрачиваемую рабочим в течение t = 5 мин. 13. Сколько времени должна действовать сила F = 500 Н, приложенная к покоящемуся телу массой m = 200 кг, если она сообщит телу скорость V = 25 м/с. Какой путь пройдет тело под действием этой силы, если оно перемещается по гладкой горизонтальной поверхности. 14. Какую силу нужно приложить к автомобилю массой m = 1500 кг, движущемуся по прямолинейному горизонтальному пути со скоростью 72 км/ч, для того, чтобы за время t = 10 с, его скорость уменьшилась до 36 км/ч? Какой путь продет при этом автомобиль? 15. C какой максимальной скоростью может вращаться в вертикальной плоскости тело массой m = 2 кг, привязанное к нити длиной L = 1 м, если нить выдерживает максимальное натяжение 400 Н. Массой нити пренебречь. 16. Найти величину линейной скорости v и ускорение а точек земной поверхности на широте С-Петербурга (город находится на широте φ = 600). Радиус земли R = 6000 км. 17. Диск, вращаясь равнозамедленно, за время t1 = 60 с уменьшил частоту своего вращения с n0 = 500 мин−1 до n1 = 0 мин−1. Найти величину ε углового ускорения диска и число оборотов N диска за это время. 18. Автомобиль, имея скорость, равную по величине v0 = 36 км/ч, за время t1 = 20 с увеличил ее до значения v1 = 72 км/ч. Определить величину ускорения и путь, пройденный автомобилем за это время, считая движение равноускоренным. 19. Первый шар массой m1 = 2 кг движется со скоростью v1 = 3 м/с. Второй шар массой m2 = 8 кг движется со скоростью v2 = 1 м/с. Найти скорость u1 первого шара и скорость u2 второго шара сразу после удара, если: а) шары движутся навстречу друг другу; б) первый шар догоняет второй. Удар считать центральным и абсолютно упругим. 20. Человек массой m1 = 60 кг, бегущий со скоростью v1 = 9 м/с, вскакивает на тележку массой m2 = 70 кг, движущуюся со скоростью v2 = 1,8 м/с. С какой скоростью u будет двигаться тележка, если: а) человек догонял тележку; б) человек бежал ей навстречу?
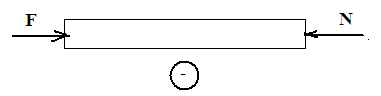
ЗАДАНИЕ 6. РАСЧЕТ НА ПРОЧНОСТЬ ПРИ РАСТЯЖЕНИИ И СЖАТИИ. Для ступенчатого стального бруса требуется: - определить значение продольной силы и нормального напряжения по длине бруса; - построить эпюры N и s; - определить абсолютное удлинение (укорочение) бруса. Модуль продольной упругости Необходимые формулы 1. Продольная сила 2. Правило знаков: внутренняя продольная сила, возникающая в поперечном сечении стержня, считается положительной, если она противодействует растяжению стержня, и отрицательной, если она противодействует его сжатию.
3. Нормальное напряжение где N - продольная сила; А (F, S) – площадь поперечного сечения. 4. Удлинение (укорочение) бруса где Е – модуль упругости материала; l – начальная длина стержня. Последовательность решения задач: 1. Разбиваем брус на участки, начинают свободного конца. Границами участков являются: начало и конец бруса, границы сечений, точки приложения сил. 2. Определить по методу сечений продольную силу для каждого участка и построить эпюру продольных сил N. Проведя параллельно оси бруса базовую (нулевую) линию эпюры, отложить перпендикулярно ей в произвольном масштабе получаемые значения. Штриховку каждого участка производить четкими перпендикулярными линиями относительно нулевой линии. 3. Для построения эпюр нормальных напряжений определяем напряжения в поперечных сечениях каждого из участков. В пределах каждого участка напряжения постоянны, то есть эпюра на данном участке изображается прямой, параллельной оси бруса. 4. Перемещение свободного конца бруса определяется как сумму удлинений (укорочений) участков бруса, вычисленных по формуле Гука. Пример решения задач на растяжение и сжатие. Условие задачи: Стальной стержень (модуль Юнга Е = 2*104 кН/см2) с размерами а = 1 м; b= 1,5 м, c = 2 м и площадью поперечного сечения нижнего участка Fн = F = 10 см2, а верхнего Fв = 2F = 20 см2 нагружен внешними осевыми силами Р1 = 100 кН и Р2 = 300 кН (рис. 6.1). Построить эпюры продольных сил N и нормальных напряжений σ. Оценить прочность стержня, если предельное напряжение (предел текучести) σт = 24 кН/см2, а допускаемый коэффициент запаса [n] = 1,5. Найти удлинение стержня ∆l. 1. Определяем значение опорной реакции Учитывая, что P2 > P1, направим опорную реакцию R вниз. Тогда из уравнения равновесия ∑Z = 0 находим: -R + P2 – P1 = 0; R = P2 – P1 =300 – 100 = 200 кН.
Рис. 6.1. Расчетная схема для задачи на растяжение и сжатие.
Оцениваем прочность стержня Сопоставляем наибольшее (по модулю) нормальное напряжение σ, которое в нашем примере возникает во втором сечении стержня, с допускаемым напряжением [ σ]. Напомним, что допускаемое напряжение представляет собой долю от предельного напряжения σпр, то есть от напряжения, при котором начинается разрушение материала. Разрушение стали, как пластичного материала, начинается при появлении значительных остаточных деформаций. Поэтому для стали предельное напряжение равно пределу текучести: σпр = σт. Тогда [ σ] = σт/[ n ] = 24/1,5 = 16кН/см2. Условие прочности имеет вид σ max ≤ [ σ] . В нашем случае σ max = 20 кН/см2 > [ σ] = 16 кН/см2, следовательно, прочность стержня на втором участке не обеспечена. Таким образом, площадь поперечного сечения стержня на втором участке необходимо увеличить. Из условия прочности определяем требуемую площадь поперечного сечения стержня на втором участке: F 2 треб ≥ N 2 / [ σ] = 200/16 = 12,5 Принимаем на втором участке F2= 12,5 см2. 5. Вычисляем удлинение всего стержня ∆l При переменных по длине стержня значениях продольной силы и площади поперечного сечения удлинение вычисляется по формуле
где E – модуль Юнга, а l – длина соответствующего участка стержня. Тогда ∆l = 10*100/2*104 – 20*150/2*104 - 10*200/2*104 = - 0,2 см. Таким образом, длина стержня уменьшается на 2 мм. Рис. 6.2. Схемы для решения задач.
Таблица 6.1. Исходные данные к задаче на растяжение и сжатие
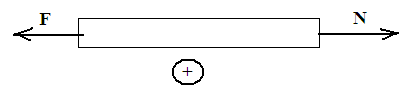
ЗАДАНИЕ 7. РАСЧЕТ НА ПРОЧНОСТЬ ПРИ СРЕЗЕ И СМЯТИИ. Элементы, которыми соединяют различные детали, например, заклепки, штифты, болты (без зазора) в основном рассчитывают на срез. Расчет носит приближенный характер и основан на следующих допущениях: 1) в поперечных сечениях рассматриваемых элементов возникает лишь один силовой фактор – поперечная сила Q; 2) при наличии нескольких одинаковых соединительных элементов каждый из них воспринимает одинаковую долю общей нагрузки, передаваемой соединением; 3) касательные напряжения распределены по сечению равномерно. На смятие, как правило, рассчитывают элементы, которые соединены заклепками, штифтами, болтами. Смятию подвергаются стенки отверстий в зонах установки соединительных элементов. Обычно расчет на смятие выполняют для соединений, соединительные элементы которых рассчитывают на срез. При расчете на смятие принимают, что силы взаимодействия между соприкасающимися деталями равномерно распределены по поверхности контакта и в каждой точке нормальны к этой поверхности. Силу взаимодействия, принято называть напряжением смятия. Расчет на прочность выполняется по формуле: σ p = где А – ширина листа, м;
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 194; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.31.82 (0.013 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

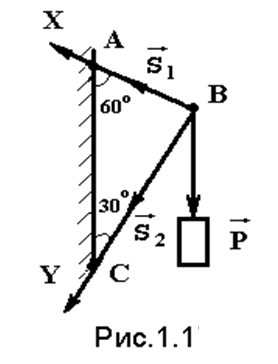 Решение. Поскольку стержни соединены в точке В, она будет служить объектом равновесия. Hа нее будет действовать сила натяжения нити, равная весу груза Р.
Решение. Поскольку стержни соединены в точке В, она будет служить объектом равновесия. Hа нее будет действовать сила натяжения нити, равная весу груза Р.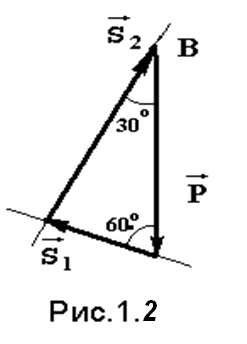 В данном решении использовался аналитический метод. Для примера приведем геометрическое решение задачи. Для этого нужно построить из сил, действующих на точку В векторный треугольник. Вначале в масштабе построим силу Р (рис.1.2). Из начала и конца этой силы проводим прямые, параллельные усилиям S1 и S2, получая, таким образом, замкнутый силовой треугольник. При этом для замыкания треугольника мы были вынуждены сменить направление усилия S2. Из треугольника, в котором усилие Р является гипотенузой, а S1 и S2 - катетами, находим:
В данном решении использовался аналитический метод. Для примера приведем геометрическое решение задачи. Для этого нужно построить из сил, действующих на точку В векторный треугольник. Вначале в масштабе построим силу Р (рис.1.2). Из начала и конца этой силы проводим прямые, параллельные усилиям S1 и S2, получая, таким образом, замкнутый силовой треугольник. При этом для замыкания треугольника мы были вынуждены сменить направление усилия S2. Из треугольника, в котором усилие Р является гипотенузой, а S1 и S2 - катетами, находим: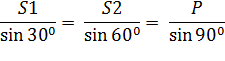
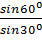 ;
;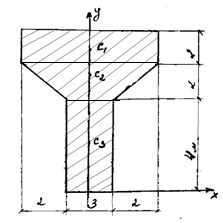 рис.3.1
рис.3.1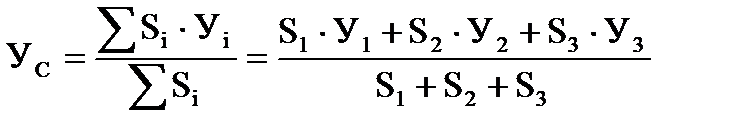
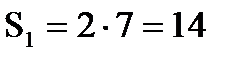 м2.
м2.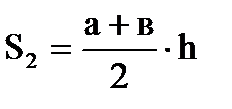
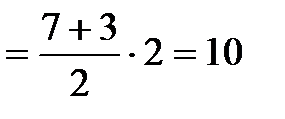 м2.
м2.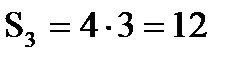 м2.
м2.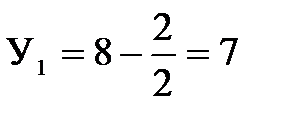 м.
м.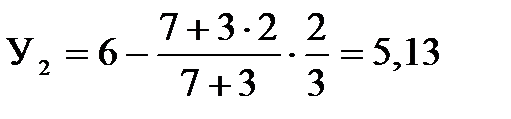 м.
м.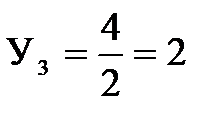 м.
м.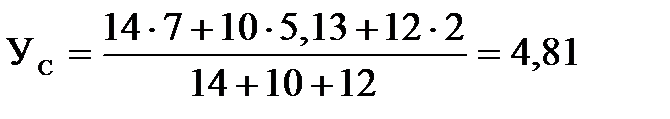 м.
м.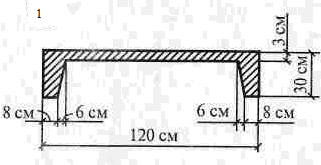
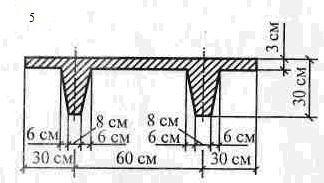
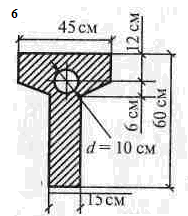
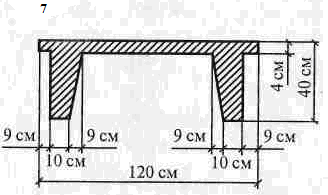
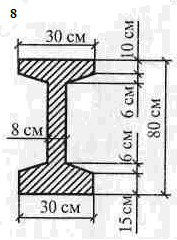
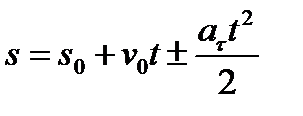 ,
S = V2 – Vo2
2a
,
S = V2 – Vo2
2a
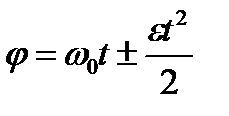 , j0=0
, j0=0
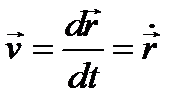
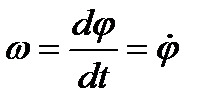
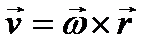 линейная скорость V = 2 πR
T
линейная скорость V = 2 πR
T
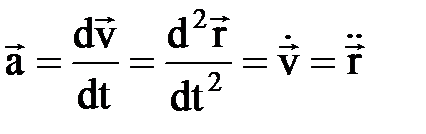
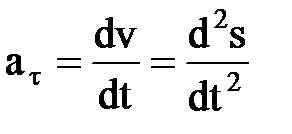
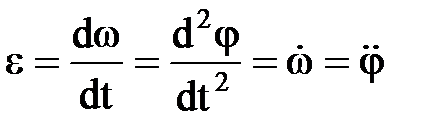
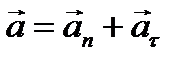
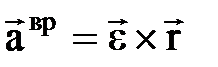 , ац=w2×R
, ац=w2×R
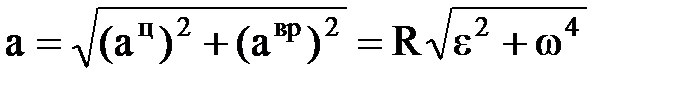
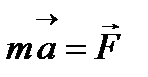
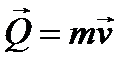
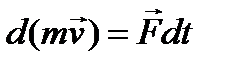
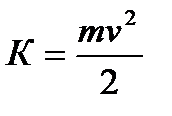
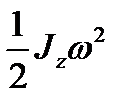
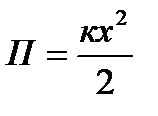
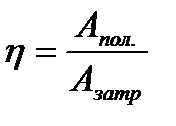
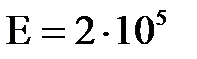 МПа.
МПа.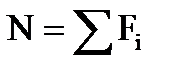 ,
,
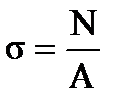 ,
,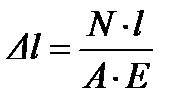 или
или 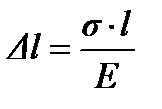 ,
,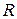 , возникающей в заделке
, возникающей в заделке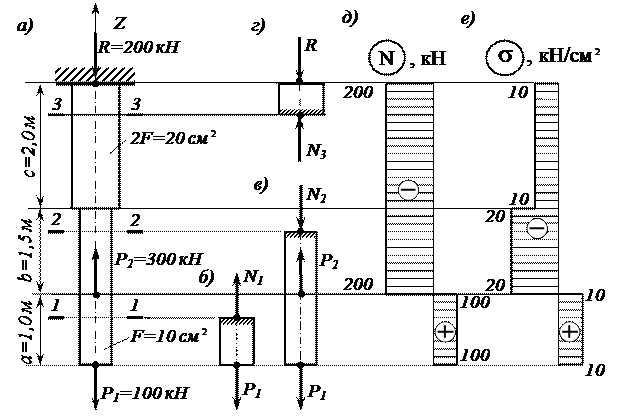
 см2.
см2.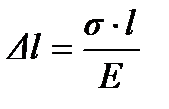

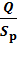 =
= 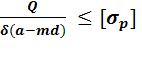 ,
,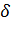 – толшина листа, м;
– толшина листа, м;


