Координаты точки в пространстве

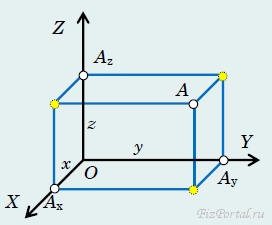
Положение точки в пространстве однозначно может быть определено с помощь  трех чисел − координат. Это утверждение является следствием того факта, что пространство, в котором мы живем, является трехмерным.
После подробного  изучения декартовых координат на прямой и на плоскости построение системы пространственных координат легко провести по аналогии. Выберем произвольно точку О − начало отсчета, через которую проведем произвольно три взаимно перпендикулярные прямые − оси координат X, Y, Z. Зададим положительные направления осей и стандартным образом введем координаты точек на этих осях (назовем их х, y, z) (рис. 6).

 

рис. 6

Декартовыми координатами произвольной точки  А в пространстве являются координаты х, y, z точек − проекций A_x, А_y, А_z на выбранные оси координат X, Y, X. Для того чтобы спроецировать точку А на ось X трехмерной системы координат, можно поступать различными способами: опустить перпендикуляр на плоскость ХОY, а затем спроецировать точку − основание этого перпендикуляра на ось X; можно и сразу опустить перпендикуляр из точки А на ось X. Еще один способ − построить прямоугольный параллелепипед с противоположными вершинами в точках А и О, ребра которого параллельны осям координат. Тогда длины этих ребер (с учетом знаков) будут являться координатами точки А.
Числа −  координаты проекций − определяются стандартным образом: модуль числа равен расстоянию до начала отсчета, а знак определяет, с какой стороны от начала отсчета лежит данная точка. Таким образом, каждой точке пространства ставится в соответствие тройка чисел − х, y, z.

Естественно, декартовая система координат в пространстве не является единственно возможной, используются и другие системы координат.

Относительность координат

Итак, мы добились поставленной цели: дали «имя», указали «точный адрес» произвольной точке пространства − каждой точке пространства поставили в однозначное соответствие набор чисел − координат. Однако знание только этих чисел не дает возможности указать конкретную точку. Эти числа-координаты имеют смысл только тогда, когда указана (известна) система отсчета − начало отсчета, направление осей и единица измерения расстояний. Только в этом случае координаты указывают на конкретную точку пространства. Если изменить систему отсчета (начало отсчета, направление осей) или единицу измерения, то изменятся и координаты всех точек. Иными словами, координаты всех точек относительны, заданы относительно оговоренной системы координат. Выбор системы координат, как мы неоднократно подчеркивали, совершенно произволен. Существенна ли эта неопределенность в выборе системы координат? Нужно ли вообще говорить о координатах, если каждый имеет полное право ввести свою собственную систему координат? Мы вынуждены примириться с этим произволом и бояться его не надо, потому что:

− иного способа математического описания положения точки в пространстве не существует;

− всегда можно в каждом конкретном случае договориться о выборе системы отсчета, тем более что часто наиболее удачный выбор системы отсчета очевиден и определяется описываемой ситуацией. Например: расположение мебели в конкретной комнате не слишком удобно проводить в системе отсчета, связанной с почтамтом, скорее всего, каждый расположит начало отсчета в одном из углов комнаты и направит оси координат вдоль «ребер» комнаты;

− произвол в выборе системы отсчета дает нам определенную свободу, дает право воспользоваться возможностью выбора в своих интересах так, чтобы в каждом конкретном случае упростить описание физического явления;

− всегда можно (и следует) найти такие физические величины, которые не зависят от выбора системы координат. Например – расстояния между точками, углы между прямыми, площади фигур;

– всегда возможно установить формулы преобразования координат при переходе из одной системы отсчета в другую.

Как видим (и в этом мы сможем убедиться неоднократно в дальнейшем), физика − наука демократичная, она предоставляет каждому «свободу выбора», только надо уметь, и не бояться, ею пользоваться. В физике существует множество законов, но «все, что не запрещено, разрешено», различные точки зрения допустимы, но вполне примиримы друг с другом либо путем компромисса, либо путем установления общих «правил игры».

Наконец, следует помнить, что в физике существуют некие «абсолютные ценности», не зависящие от выбранной точки зрения.

1.5. Преобразования координат

Рассмотрим, как будут изменяться координаты точек при различных преобразованиях системы отсчета. Первый пример − изменение единицы измерения длины при неизменных начале отсчета и направлениях осей координат. Так как координаты точки представляют собой расстояния от проекций точки на оси координат до начала отсчета, то при изменении единицы измерения длины координаты будут изменяться так же, как изменяется численное значение длин и расстояний, то есть умножаться на коэффициент, связывающий различные единицы измерения. При изменении направления оси очевидно, что соответствующие координаты изменят знак на противоположный.

Получим теперь формулы преобразования координат при  сдвиге начала отсчета. Пусть на плоскости введены две системы декартовых координат ХОY и Х^/О^/Y^/, оси которых попарно параллельны (рис. 7)

 

рис. 7

Обозначим координаты точки О^/ в системе отсчета ХОY через х_o и у_o. Пусть координаты произвольной точки А в системе отсчета Х^/О^/Y^/ равны х^/ и у^/. Тогда, как следует из рисунка, координаты х, у этой же точки в системе отсчета ХОУ могут быть найдены по формулам

x₁ = x_o + x^/; y₁ = y_o + y^/. (1)

 

Легко записать формулы  обратного перехода от координат в системе отсчета ХОY к координатам в системе отсчета Х^/О^/Y^/:

x^/ = −x_o + x; y^/ = −y_o + y. (2)

 

Как и следовало ожидать, формулы обратного  преобразования (2) полностью аналогичны формулам (1), так как −х_o и −у_o есть координаты точки О в системе отсчета Х^/О^/Y^/. Эти формулы называют преобразованиями сдвига. Назовем систему отсчета ХОY исходной, а систему отсчета Х^/О^/Y^/ смещенной. (Очевидно, что эти названия условны, так как две рассматриваемые системы равноправны, и их можно поменять местами.)

Тогда правила преобразований сдвига можно сформулировать следующим образом: при смещении начала координат координаты всех точек уменьшаются на величину соответствующего смещения начала отсчета; координата точки в смещенной системе координат равна координате в исходной системе минус соответствующая координата начала отсчета смещенной системы.

  Упражнение.
Получите формулы преобразования сдвига для  одномерного и трехмерного случаев.

Существенным является тот факт, что в любом случае, при любом изменении  системы отсчета можно найти формулы преобразования координат. Следовательно, если положение тела описано в одной системе отсчета, то оно описано и в любой другой.