Математическое описание равномерного движения

Пусть некоторое тело, которое можно считать  материальной точкой, движется вдоль заданной прямой. Для описания его движения направим ось X декартовой системы координат вдоль этой прямой (которая является траекторией движения), выберем также на этой оси начало отсчета. Положение тела однозначно определяется одной координатой, поэтому закон движения в данном случае представляет собой одну функцию − зависимость координаты х от времени t − x(t). Рассмотрим наиболее простой вид движения − равномерное.

Равномерным называется такое движение точки, при котором за любые равные промежутки времени она проходит равные пути.

При таком движении легко определить физическую характеристику быстроты движения − скорость.

Путевой скоростью равномерного движения называется отношение пути, пройденного телом, к интервалу времени, за который этот путь пройден.

В дальнейшем мы определим скорость несколько по-другому, поэтому в данном определении мы оговорили термин «путевая скорость».

Если обозначить пройденный путь S, а интервал времени t, то скорость¹ v, как вам известно, определяется формулой

v = S/t. (1)

При равномерном движении это отношение не зависит от рассматриваемого промежутка времени, так как пройденный путь пропорционален временному интервалу. Можно дать еще одно истолкование скорости: скорость тела равна пути, пройденному телом за единицу времени².

Скорость есть физическая величина, имеющая в системе СИ размерность м/с (метр в секунду). Кроме этой единицы измерения скорости довольно часто используется внесистемная единица − км/ч, а в некоторых странах − миль/ч.

Величина пройденного пути S показывает, на сколько сместилось тело, но не указывает направление этого смещения. Используя введенные координаты, можно определить смещение тела как изменение его координаты:

Δх = х − х_o, (2)

где х − координата тела в некоторый момент времени t, а х_o − координата тела в начальный момент t_o.

Символом Δ (греческая буква «дельта») мы будем обозначать изменение любой физической величины (в данном случае координаты) − конечное значение минус начальное; такое обозначение является общепринятым.
Изменение координаты может быть как положительным (при увеличении значения координаты), так и отрицательным (при ее уменьшении). Таким образом, знак величины Δх просто указывает направление движения в положительном либо отрицательном направлении оси X. Очевидно, что путь, пройденный материальной точкой при движении вдоль оси в одном направлении, связан с изменением координаты соотношением

S = |Δх|. (3)

Таким образом, если вместо пути использовать изменение координаты, то с помощью знака ± (плюс − минус) можно указать дополнительно и направление движения. Соответствующим образом можно переопределить и скорость движения: скорость равномерного движения вдоль прямой равна отношению изменения координаты к промежутку времени, в течение которого это изменение произошло:

v = (x − x_o)/(t − t_o) = Δ x/ Δ t. (4)

Заметьте, для величины интервала времени мы также используем обозначение Δt − разность между показаниями часов в конечный и начальный моменты времени. В данном определении скорость может быть положительной (если тело движется в положительном направлении оси) и отрицательной (при движении в противоположном направлении). Таким образом, знак скорости указывает направление движения, а ее модуль сохраняет прежнее значение путевой скорости − путь, пройденный в единицу времени.

Найдем теперь зависимость координаты от времени (закон движения) при равномерном движении вдоль прямой, то есть в том случае, когда скорость остается постоянной величиной. Непосредственно из формулы, определяющей скорость, движение можно выразить так:

х = х_o + v(t − t_o). (5)

Эта формула дает закон движения материальной точки при ее равномерном движении вдоль прямой. Знание только скорости движения не позволяет однозначно определить его закон − необходимо знать положение (то есть координату) тела в какой-нибудь момент времени. Часто это дополнительное условие называют начальным: в начальный момент времени t_o тело находится в точке с координатой х_o. Однако совсем не обязательно, чтобы движение начиналось в момент времени t_o − формулу (5) можно применять для любого времени t (в том числе и t < t_o), важно только, чтобы во все рассматриваемые моменты времени продолжалось движение с той же скоростью. В этом смысле закон движения обратим − его можно использовать как для того, чтобы предсказать положение тела в будущем (t > t_o), так и для того, чтобы определить, где оно находилось в прошлом (t < t_o).

При рассмотрении системы координат мы неоднократно подчеркивали, что выбор начала отсчета координат произволен, также произволен и выбор начала отсчета времени t_o. Физический смысл этого «произвола»: вы можете «запустить» свои часы в любой удобный для вас момент времени. Поэтому часто в формуле закона движения полагают, что t_o = 0, тогда

х = х_o + vt. (6)

Различие между формулами (5) и (6) при описании одного и того же движения только в начальном отсчете времени: при описании движения с помощью формулы (5) полагают, что тело находилось в точке с координатой х_o при t = t_o, а в формуле (6) − при t = 0.

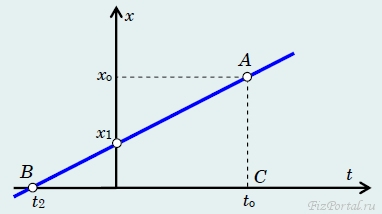
С математической точки зрения закон движения является функцией и, как всякая функция, может быть проиллюстрирован графиком. Графическое представление различных законов наглядно, информативно и чрезвычайно распространено как в физике, так и в других естественных науках.

Построим график функции, описываемой уравнением (5). Зависимость х(t) в данном случае линейна, поэтому ее график является прямой линией (рис. 34).

 

рис. 34

Эта прямая проходит через точку³ А с координатами (t_o, х_o). Точки пересечения графика с осями координат также имеют наглядный физический смысл: х₁ − положение тела в момент времени t = 0; t₂ − момент времени, когда тело находилось в точке начала отсчета.

Наклон графика определяется скоростью точки − чем выше скорость, тем больший угол образует график с осью t.

Иногда говорят, что скорость численно равна тангенсу угла наклона графика закона движения к оси времени. Действительно, в прямоугольном треугольнике АBС длина отрезка ВС равна Δt, а длина отрезка АС равна Δ х. Следовательно, их отношение, с одной стороны, равно скорости движения

v = Δx/Δt,

с другой − тангенсу угла ∠ АВС. Однако к этому утверждению следует относиться с большой осторожностью, так как изменения координаты Δх и времени Δt являются физическими величинами и имеют разные размерности, поэтому масштабы соответствующих осей могут выбираться произвольно, независимо друг от друга. Изменение масштаба одной из осей приведет к изменению угла наклона графика, скорость же при этом, конечно, не изменится. Поэтому измерять скорость с помощью транспортира неразумно. Поэтому «тангенс наклона» Δx/Δt следует понимать как отношение физических величин, а не длин отрезков, на рисунке с произвольным масштабом. Во избежание подобной путаницы в дальнейшем для обозначения отношения Δx/Δt мы будем использовать термин «коэффициент наклона».

 

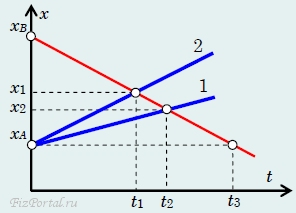
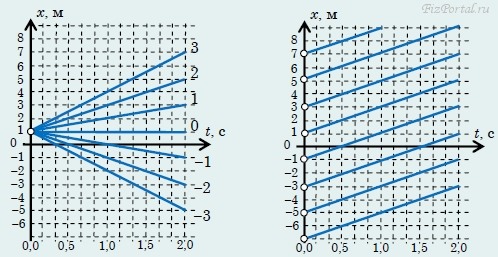
рис. 35

На рис. 35 приведены графики законов движения нескольких человек вдоль одной прямой, причем их движение может быть словесно описано следующим образом: «Из пункта А (расположенного в точке с координатой х_A) одновременно вышли два пешехода, причем второй двигался со скоростью в два раза большей скорости первого. Навстречу им из пункта В (расположенного в точке с координатой х_B) вышел третий пешеход со скоростью, равной скорости второго. Третий пешеход встретил второго в момент времени t₁ в точке с координатой х₁, а затем первого в момент времени t₂ в точке с координатой х₂. В момент времени t₃ он прибыл в пункт А». Вот такая «история» изображена на этом графике! Согласитесь, графический способ описания гораздо короче и нагляднее. Если закон равномерного движения выражается функцией

х = х_o + vt,

то график этой функции − прямая линия, причем параметр v (скорость) определяет наклон графика (на рис. 36 значения скорости в м/с указаны справа, здесь х_o = 1,0 м), а изменение параметра х_o приводит к сдвигу графика вдоль оси X (на рис. 37 v = 2,0 м/с, а начальная координата хo совпадает с разметкой оси).

¹У нас начинают проявляться недостатки разговорного языка: «материальная точка (модель тела) находится в точке (положение тела в пространстве) с координатой х_o, что соответствует точке А (точка на рисунке) на графике закона движения». Эти недостатки создают определенные трудности, однако в большинстве случаев из смысла фразы понятно, о каких точках и координатах идет речь.

²Хотя обозначения физических величин, в принципе, произвольны, имеется ряд обозначений традиционных, общепринятых. К числу таких относится и традиционное обозначение скорости латинской буквой v, что соответствует английскому слову velocity − скорость.

³В принципе, можно ввести и иную характеристику быстроты передвижения − величину, обратную скорости, − отношение t/S, смысл которой − путь, пройденный за единицу времени. Согласитесь, что такая величина также характеризует движение и иногда используется в жизни: километр пробежал за три минуты. Однако более удобной физической величиной является все-таки скорость.