Ускорение при движении точки по прямой

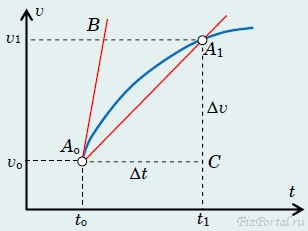
После того как мы разобрались с понятием мгновенной скорости (скорости в данный момент времени), у нас появилась возможность говорить об изменении скорости, определить физическую величину, описывающую это изменение. Пусть в момент времени t_o скорость точки была v_o, а в момент времени t₁ > t_o стала равной v₁. Тогда отношение изменения скорости к промежутку времени, в течение которого это изменение произошло, называется ускорением точки¹:

a = (v₁ − v₂)/(t₁ − t_o) = Δ v/ Δ t. (1)

Можно сказать, что ускорение − это скорость  изменения скорости тела.

Ускорение − физическая величина, размерность которой есть отношение размерности скорости к размерности времени, поэтому в СИ размерность ускорения

[a] = [v]/[t] = (м/с)/с = м/с²,

то есть «метр разделить на секунду в квадрате», или «метр в секунду за секунду».

Обсуждая данное определение, мы должны повторить все наши рассуждения, касающиеся перехода от понятия средней к понятию мгновенной скорости. Так, возможны ситуации, когда отношение Δv/Δt не зависит от величины интервала Δt − в этом случае ускорение является постоянной величиной и такое движение называется равноускоренным. Если же величина Δv/Δt зависит от промежутка времени, то формула (1) дает значение среднего ускорения на интервале времени от t_o до t₁. Для более детального описания движения необходимо рассмотреть предельный переход к малому промежутку времени. В этом случае предельное значение отношения Δv/Δt будет являться мгновенным ускорением, или ускорением «в данный момент времени».

При таком определении необходимо повторить все замечания о математическом и физическом смысле предельного перехода Δt → 0, однако они полностью аналогичны рассуждениям о мгновенной скорости, поэтому проведите их самостоятельно.

Заметим, что ускорение, как и скорость, может быть как положительным, так и отрицательным. Напомним, что знак скорости указывает направление движения. Смысл знака ускорения иной − он показывает направление изменения скорости. Рассмотрим возможные комбинации знаков скорости и ускорения.

l) v > 0, a > 0: тело движется в положительном направлении выбранной оси, изменение скорости также положительно, то есть скорость возрастает, иными словами − тело ускоряется.

2) v > 0, а < 0: тело движется в положительном направлении оси, но его скорость убывает − тело притормаживает.

3) v < 0, а > 0: тело движется в отрицательном направлении, но его скорость увеличивается, следовательно, уменьшается по абсолютной величине: тело, двигаясь в отрицательном направлении, притормаживает.

4) v < 0, а < 0: тело движется в отрицательном направлении, при этом его скорость уменьшается, но по абсолютной величине возрастает − тело движется ускоряясь.

Рассмотрим теперь геометрический смысл мгновенного ускорения. Для этого построим график зависимости v_o скорости от времени для некоторой движущейся точки (на рис. 46 − плавная кривая A_oA₁).

 

рис. 46

Пусть в момент времени  t_o скорость тела равна v_o (точка А_o на графике), а в момент времени t₁ − скорость v₁ (точка А₁ на графике). В прямоугольном треугольнике А_oA₁С отношение длин катетов

|A₁C|/|A_oC| = Δv/Δt

(то есть среднее ускорение) численно равно тангенсу угла наклона секущей A_oA₁ к оси времени.

При уменьшении интервала времени (то есть при t₁ → t_o) секущая А_oА₁ стремится к касательной А_oВ. Следовательно, тангенс угла наклона касательной к графику зависимости скорости от времени численно равен мгновенному ускорению.

Обязательно следует отметить, что к выражению «тангенс угла наклона» (как и в случае скорости) необходимо относиться с физической, а не с геометрической точки зрения: длины рассматриваемых катетов являются физическими величинами, имеющими различную размерность, поэтому и «тангенс» имеет размерность, в данном случае, ускорения. Поэтому в дальнейшем мы будем использовать термин «коэффициент наклона» касательной к оси времени.

¹Мы будем обозначать ускорение латинской буквой a как сокращение английского слова acceleration − ускорение (кстати, слово «акселерация» происходит от того же корня).