
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 3. Плоскопараллельное движение твердого тела. Определение скоростей и ускорений.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Лекция 3. Плоскопараллельное движение твердого тела. Определение скоростей и ускорений. В данной лекции рассматриваются следующие вопросы: 1. Плоскопараллельное движение твердого тела. 2. Уравнения плоскопараллельного движения. 3. Разложение движения на поступательное и вращательное. 4. Определение скоростей точек плоской фигуры. 5. Теорема о проекциях скоростей двух точек тела. 6. Определение скоростей точек плоской фигуры с помощью мгновенного центра скоростей. 7. Решение задач на определение скорости. 8. План скоростей. 9. Определение ускорений точек плоской фигуры. 10. Решение задач на ускорения. 11. Мгновенный центр ускорений. Изучение данных вопросов необходимо в дальнейшем для динамики плоского движения твердого тела, динамики относительного движения материальной точки, для решения задач в дисциплинах «Теория машин и механизмов» и «Детали машин».
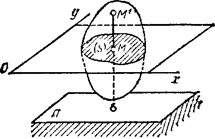
Плоскопараллельное движение твердого тела. Уравнения плоскопараллельного движения. Разложение движения на поступательное и вращательное Плоскопараллельным (или плоским) называется такое движение твердого тела, при, котором все его точки перемещаются параллельно некоторой фиксированной плоскости П (рис. 28). Плоское движение совершают многие части механизмов и машин, например катящееся колесо на прямолинейном участке пути, шатун в кривошипно-ползунном механизме и др. Частным случаем плоскопараллельного движения является вращательное движение твердого тела вокруг неподвижной оси.
Рис.28 Рис.29
Рассмотрим сечение S тела какой-нибудь плоскости О xy, параллельной плоскости П (рис.29). При плоскопараллельном движении все точки тела, лежащие на прямой ММ ’, перпендикулярной течению S, т. е. плоскости П, движутся тождественно. Отсюда заключаем, что для изучения движения всего тела достаточно изучить, как движется в плоскости Оху сечение S этого тела или некоторая плоская фигура S. Поэтому в дальнейшем вместо плоского движения тела будем рассматривать движение плоской фигуры S в ее плоскости, т.е. в плоскости Оху. Положение фигуры S в плоскости Оху определяется положением какого-нибудь проведенного на этой фигуре отрезка АВ (рис. 28). В свою очередь положение отрезка АВ можно определить, зная координаты x A и y A точки А и угол
При движении фигуры величины x A и y A и
Уравнения, определяющие закон происходящего движения, называются уравнениями движения плоской фигуры в ее плоскости. Они же являются уравнениями плоскопараллельного движения твердого тела. Первые два из уравнений движения определяют то движение, которое фигура совершала бы при Основными кинематическими характеристиками рассматриваемого движения являются скорость и ускорение поступательного движения, равные скорости и ускорению полюса
Рис.30 Рис.31 Рис.32
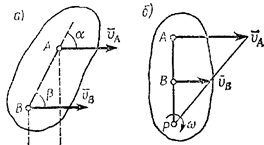
Один из таких методов дает теорема: проекции скоростей двух точек твердого тела на ось, проходящую через эти точки, равны друг другу. Рассмотрим какие-нибудь две точки А и В плоской фигуры (или тела). Принимая точку А за полюс (рис.32), получаем
Рис.33 Если теперь в момент времени
так как
Из равенств, следует еще, что
Полученные результаты приводят к следующим выводам. 1. Для определения мгновенного центра скоростей надо знать только направления скоростей 2. Для определения скорости любой точки плоской фигуры, надо знать модуль и направление скорости какой-нибудь одной точки А фигуры и направление скорости другой ее точки В. Тогда, восставив из точек А и В перпендикуляры к 3. Угловая скорость
Рассмотрим некоторые частные случаи определения мгновенного центра скоростей. а) Если плоскопараллельное движение осуществляется путем качения без скольжения одного цилиндрического тела по поверхности другого неподвижного, то точка Р катящегося тела, касающаяся неподвижной поверхности (рис.34), имеет в данный момент времени вследствие отсутствия скольжения скорость, равную нулю ( б) Если скорости точек А и В плоской фигуры параллельны друг другу, причем линия АВ не перпендикулярна
Рис.34
Рис.35 в) Если скорости точек А и В плоской фигуры параллельны друг другу и при этом линия АВ перпендикулярна г) Если известны вектор скорости
Рис.36
Определим скорости точек А,В и С. Мгновенный центр скоростей находится в точке касания катушки с плоскостью. Скорость полюса С .
Скорости точек А и В направлены перпендикулярно отрезкам прямых, соединяющих эти точки с мгновенным центром скоростей. Величина скоростей:
Пример 9. Стержень АВ скользит концами по взаимно перпендикулярным прямым так, что при угле
Рис.37
Нетрудно определить направление вектора скорости точки А, скользящей по вертикальной прямой. Тогда Угловая скорость Скорость точки А:
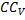 и равна: и равна:
План скоростей. Пусть известны скорости нескольких точек плоского сечения тела (рис.38). Если эти скорости отложить в масштабе из некоторой точки О и соединить их концы прямыми, то получится картинка, которая называется планом скоростей. (На рисунке
Рис.38
Свойства плана скоростей.
Действительно, б) Стороны плана скоростей пропорциональны соответствующим отрезкам прямых на плоскости тела. Так как Объединив оба свойства, можно сделать вывод, что план скоростей подобен соответствующей фигуре на теле и повёрнут относительно её на 90˚ по направлению вращения. Эти свойства плана скоростей позволяют определять скорости точек тела графическим способом. Пример 10. На рисунке 39 в масштабе изображён механизм. Известна угловая скорость
Рис.39
Чтобы построить план скоростей должна быть известна скорость какой-нибудь одной точки и хотя бы направление вектора скорости другой. В нашем примере можно определить скорость точки А:
Рис.40
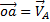 Известно направление вектора скорости ползуна В – горизонтальное. Проводим на плане скоростей из точки О прямую I по направлению скорости Известно направление вектора скорости ползуна В – горизонтальное. Проводим на плане скоростей из точки О прямую I по направлению скорости 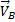 , на которой должна находиться точка b, определяющая скорость этой точки В. Так как стороны плана скоростей перпендикулярны соответствующим звеньям механизма, то из точки а проводим прямую перпендикулярно АВ до пересечения с прямой I. Точка пересечения определит точку b, а значит и скорость точки В: , на которой должна находиться точка b, определяющая скорость этой точки В. Так как стороны плана скоростей перпендикулярны соответствующим звеньям механизма, то из точки а проводим прямую перпендикулярно АВ до пересечения с прямой I. Точка пересечения определит точку b, а значит и скорость точки В: 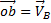 . По второму свойству плана скоростей его стороны подобны звеньям механизма. Точка С делит АВ пополам, значит и с должна делить а b пополам. Точка с определит на плане скоростей величину и направление скорости . По второму свойству плана скоростей его стороны подобны звеньям механизма. Точка С делит АВ пополам, значит и с должна делить а b пополам. Точка с определит на плане скоростей величину и направление скорости 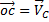 (если с соединить с точкой О). (если с соединить с точкой О).
Скорость точки Е равна нулю, поэтому точка е на плане скоростей совпадает с точкой О. Далее. Должно быть Рис.41 Рис.42
Наконец, когда точка М движется криволинейно и ее траектория известна, то
Рис.43
Угловую скорость находим с помощью мгновенного центра скоростей:
Угловое ускорение при таком движении можно найти как производную от угловой скорости. Имея в виду, что
Если С – полюс, то
Величину ускорения найдём с помощью проекций на оси х и у:
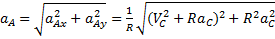 . .
Ускорение мгновенного центра скоростей где И, так как Таким образом, ускорение мгновенного центра скоростей не равно нулю. Пример 12. Вернёмся к примеру 9 (рис. 44).
Рис.44
Найдём ускорение точки А, полагая Имеем:
Где Предположим, что вектор Ускорение
Из второго уравнения сразу находим ускорение точки А
Положительное значение Из первого уравнения можно найти ускорение
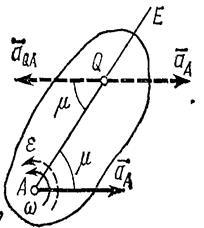
Мгновенный центр ускорений. При непоступательном движении плоской фигуры у нее в каждый момент времени имеется точка Q, ускорение которой равно нулю. Эта точка называется мгновенным центром ускорений. Определяется положение центра Q, если известны ускорение 1) находим значение угла 2) от точки А под углом при этом прямая АЕ должна быть отклонена от 3) откладываем вдоль линии АЕ отрезок AQ, равный
Рис.45
Построенная таким путем точка Q и будет мгновенным центром ускорений. В самом деле, известно что
где численно Если точку Q выбрать за полюс, то так как
При этом численно
Следовательно, ускорения точек плоской фигуры определяются в данный момент времени так, как если бы движение фигуры, было вращением вокруг мгновенного центра ускорений Q. При этом
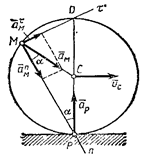
т.е. ускорения точек плоской фигуры пропорциональны их расстояниям от мгновенного центра ускорений. Картина распределения ускорений точек плоской фигуры в данный момент времени показана на рис.46. Следует иметь в виду, что положения мгновенного центра скоростей Р и мгновенного центра ускорений Q в данный момент времени не совпадают. Например, если колесо катится по прямолинейному рельсу (см. рис.47), причем скорость его центра С постоянна (
Рис.46 Рис.47
Мгновенный центр ускорений в этом случае находится, очевидно, в точке С, так как она движется равномерно и прямолинейно и Понятием о мгновенном центре ускорений удобно пользоваться при решении некоторых задач.
Вопросы для самопроверки - Какое движение твердого тела называется плоским? Приведите примеры звеньев механизмов, совершающих плоское движение. - Из каких простых движений складывается плоское движение твердого тела? - Как определяется скорость произвольной точки тела при плоском движении? - Какое движение твердого тела называется плоскопараллельным? - Какими уравнениями задается плоскопараллельное движение? - Как по уравнениям движения плоской фигуры найти скорость полюса и угловую скорость вращения вокруг полюса? - Как определить скорость любой точки плоской фигуры? - Сформулируйте теорему о проекциях скоростей двух точек плоской фигуры. - Какие способы применяют для определения скоростей точек тела при плоскопараллельном движении? - Что такое мгновенный центр скоростей? Как определяется величина и направление скорости произвольной точки тела при известном положении мгновенного центра скоростей и угловой скорости? - Из каких составляющих складывается ускорение точки при плоском движении? - Запишите формулы для вычисления касательной и нормальной составляющих относительного ускорения точки при плоском движении тела. - Приведите определение мгновенного центра ускорений. - При плоском движении тела в некоторый момент времени оказалось, что его точки А и В отстоят от мгновенного центра ускорений на расстояниях 5 и 10 см. Чему равен модуль ускорения точки В, если модуль ускорения точки А равен 3 м/с2? - Зависят ли поступательное перемещение плоской фигуры и ее поворот от выбора полюса? - Как определяется скорость любой точки плоской фигуры? - Покажите, что проекции скоростей точек неизменяемого отрезка на ось, совпадающую с этим отрезком, равны между собой. - Что представляет собой отрезок, соединяющий две вершины плана скоростей? - Какие минимальные данные необходимы для построения плана скоростей? - Какую точку плоской фигуры называют называют мгновенным центром скоростей и каковы основные случаи определения его положения? - Что представляет собой распределение скоростей точек плоской фигуры в данный момент? - Как построить центр поворота плоской фигуры, зная ее начальное и конечное положения? - Что представляет собой неподвижная и подвижная центроиды и что происходит с центроидами при действительном движении плоской фигуры? - Как определяется ускорение любой точки плоской фигуры? - Сформулируйте теорему об ускорениях точек плоской фигуры. - Почему проекция ускорения любой точки плоской фигуры на ось, проходящую через эту точку из полюса, не может быть больше проекции ускорения полюса на эту ось? - Какую точку плоской фигуры называют мгновенным центром ускорений и может ли мгновенный центр ускорений совпадать с мгновенным центром скоростей? - Перечислите известные вам способы определения положения мгновенного центра ускорений? - Что представляет собой картина распределения ускорений точек плоской фигуры в данный момент времени в трех случаях а) б) в) - Как производят определение ускорений точек и угловых ускорений звеньев плоского механизма?
Лекция 3. Плоскопараллельное движение твердого тела. Определение скоростей и ускорений. В данной лекции рассматриваются следующие вопросы: 1. Плоскопараллельное движение твердого тела. 2. Уравнения плоскопараллельного движения. 3. Разложение движения на поступательное и вращательное. 4. Определение скоростей точек плоской фигуры. 5. Теорема о проекциях скоростей двух точек тела. 6. Определение скоростей точек плоской фигуры с помощью мгновенного центра скоростей. 7. Решение задач на определение скорости. 8. План скоростей. 9. Определение ускорений точек плоской фигуры. 10. Решение задач на ускорения. 11. Мгновенный центр ускорений. Изучение данных вопросов необходимо в дальнейшем для динамики плоского движения твердого тела, динамики относительного движения материальной точки, для решения задач в дисциплинах «Теория машин и механизмов» и «Детали машин».
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 411; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.89.0 (0.015 с.) |

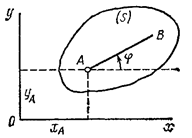
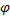 , который отрезок АВ образует с осью х. Точку А, выбранную для определения положения фигуры S, будем в дальнейшем называть полюсом.
, который отрезок АВ образует с осью х. Точку А, выбранную для определения положения фигуры S, будем в дальнейшем называть полюсом.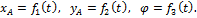
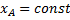 и
и 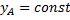 , т.е. когда полюс А неподвижен; это будет вращение фигуры вокруг полюса А. Отсюда можно заключить, что в общем случае движение плоской фигуры в ее плоскости может рассматриваться как слагающееся из поступательного движения, при котором все точки фигуры движутся так же, как полюс А, и из вращательного движения вокруг этого полюса.
, т.е. когда полюс А неподвижен; это будет вращение фигуры вокруг полюса А. Отсюда можно заключить, что в общем случае движение плоской фигуры в ее плоскости может рассматриваться как слагающееся из поступательного движения, при котором все точки фигуры движутся так же, как полюс А, и из вращательного движения вокруг этого полюса.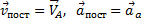 , а также угловая скорость
, а также угловая скорость 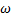 и угловое ускорение
и угловое ускорение 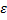 вращательного движения вокруг полюса.
вращательного движения вокруг полюса.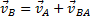 . Отсюда, проектируя обе части равенства на ось, направленную по АВ, и учитывая, что вектор
. Отсюда, проектируя обе части равенства на ось, направленную по АВ, и учитывая, что вектор 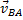 перпендикулярен АВ, находим
перпендикулярен АВ, находим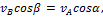 и теорема доказана.
и теорема доказана.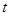 взять точку Р за полюс, то скорость точки А будет
взять точку Р за полюс, то скорость точки А будет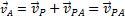 ,
,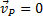 . Аналогичный результат получается для любой другой точки фигуры. Следовательно, скорости точек плоской фигуры определяются в данный момент времени так, как если бы движение фигуры было вращением вокруг мгновенного центра скоростей. При этом
. Аналогичный результат получается для любой другой точки фигуры. Следовательно, скорости точек плоской фигуры определяются в данный момент времени так, как если бы движение фигуры было вращением вокруг мгновенного центра скоростей. При этом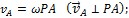
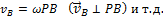
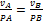 точек плоской фигуры пропорциональны их расстояниям от МЦС.
точек плоской фигуры пропорциональны их расстояниям от МЦС.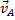 и
и 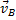 каких-нибудь двух точек А и В плоской фигуры (или траектории этих точек); мгновенный центр скоростей находится в точке пересечения перпендикуляров, восставленных из точек А и В к скоростям этих точек (или к касательным к траекториям).
каких-нибудь двух точек А и В плоской фигуры (или траектории этих точек); мгновенный центр скоростей находится в точке пересечения перпендикуляров, восставленных из точек А и В к скоростям этих точек (или к касательным к траекториям).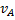 , найдем скорость
, найдем скорость 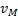 любой точки М плоской фигуры. Направлен вектор
любой точки М плоской фигуры. Направлен вектор 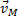 перпендикулярно РМ в сторону поворота фигуры.
перпендикулярно РМ в сторону поворота фигуры.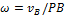 .
.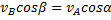 т. е.
т. е. 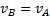 ; аналогичный результат получается для всех других точек. Следовательно, в рассматриваемом случае скорости всех точек фигуры в данный момент времени равны друг другу и по модулю, и по направлению, т.е. фигура имеет мгновенное поступательное распределение скоростей (такое состояние движения тела называют еще мгновенно поступательным). Угловая скорость
; аналогичный результат получается для всех других точек. Следовательно, в рассматриваемом случае скорости всех точек фигуры в данный момент времени равны друг другу и по модулю, и по направлению, т.е. фигура имеет мгновенное поступательное распределение скоростей (такое состояние движения тела называют еще мгновенно поступательным). Угловая скорость 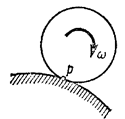
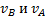 .
.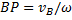 .
.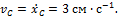
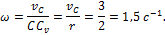
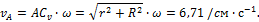
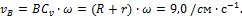
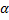 скорость
скорость 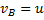 . Длина стержня AB= l. Определим скорость конца А и угловую скорость стержня.
. Длина стержня AB= l. Определим скорость конца А и угловую скорость стержня.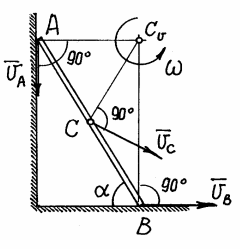
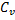 находится на пересечении перпендикуляров к
находится на пересечении перпендикуляров к 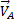 и
и 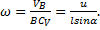
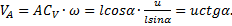
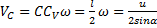 .
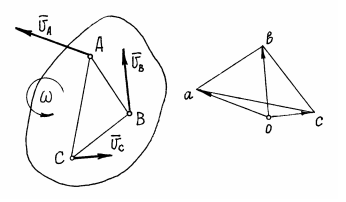
.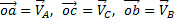 ).
).
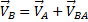 . Но на плане скоростей
. Но на плане скоростей 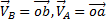 . Значит
. Значит 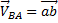 причём
причём 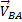 перпендикулярна АВ, поэтому и
перпендикулярна АВ, поэтому и 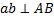 . Точно так же
. Точно так же 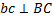 и
и 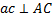 .
.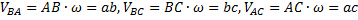 , то отсюда и следует, что стороны плана скоростей пропорциональны отрезкам прямых на плоскости тела.
, то отсюда и следует, что стороны плана скоростей пропорциональны отрезкам прямых на плоскости тела.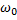 звена ОА.
звена ОА.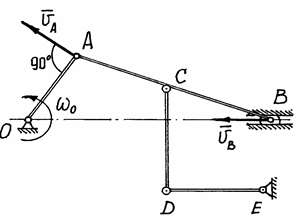
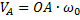 и направление её вектора
и направление её вектора 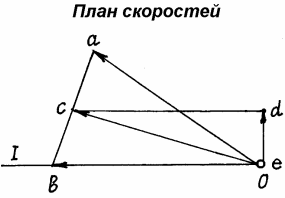
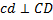 и
и 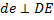 . Проводим эти прямые, находим их точку пересечения d. Отрезок о d определит вектор скорости
. Проводим эти прямые, находим их точку пересечения d. Отрезок о d определит вектор скорости 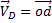 .
.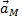 можно заменить суммой
можно заменить суммой 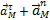 .
.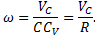
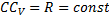 , а точка С движется по прямой, получим
, а точка С движется по прямой, получим 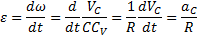
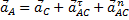 , где
, где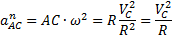
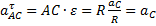 .
.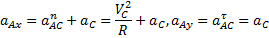
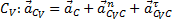 ,
,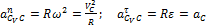 .
. 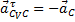 , ускорение
, ускорение 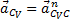 и
и 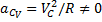 .
.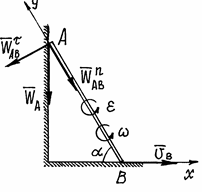
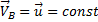 т.е.
т.е. 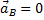
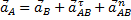 , (1)
, (1)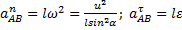 , но направление вектора
, но направление вектора 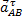 неизвестно, неизвестно и угловое ускорение
неизвестно, неизвестно и угловое ускорение 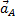 , конечно, направлено по траектории прямолинейного движения точки А, предположим вниз. Спроектируем векторное равенство (1) на оси х и у, получим:
, конечно, направлено по траектории прямолинейного движения точки А, предположим вниз. Спроектируем векторное равенство (1) на оси х и у, получим: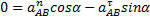 и
и 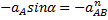 .
.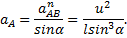
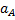 указывает на то, что направление вектора
указывает на то, что направление вектора 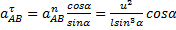 и угловое ускорение
и угловое ускорение 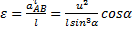 (направления
(направления 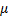 , из формулы
, из формулы 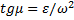 ;
; 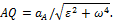
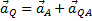 ,
,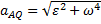 . Подставляя сюда значение AQ находим, что
. Подставляя сюда значение AQ находим, что 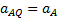 . Кроме того, вектор
. Кроме того, вектор 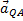 должен образовывать с линией AQ угол
должен образовывать с линией AQ угол 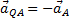 и
и 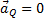 .
. 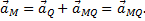
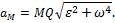
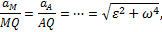
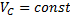 ), то мгновенный центр скоростей находится в точке Р (
), то мгновенный центр скоростей находится в точке Р (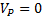 ), но при этом, как было показано
), но при этом, как было показано 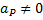 ; следовательно, точка Р не является одновременно мгновенным центром ускорений.
; следовательно, точка Р не является одновременно мгновенным центром ускорений.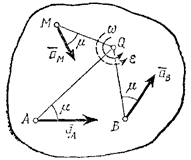
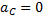 . Центры скоростей и ускорений совпадают тогда, когда фигура (тело) вращается вокруг неподвижной оси.
. Центры скоростей и ускорений совпадают тогда, когда фигура (тело) вращается вокруг неподвижной оси.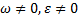 ;
;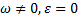 ;
;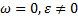 .
.


