Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства растворов жидких летучих компонентов. Перегонка.Содержание книги
Поиск на нашем сайте
Жидкие бинарные смеси представляют собой растворы двух жидких летучих компонентов. Летучими называются жидкости, имеющие при комнатной температуре высокое давление пара (относительно низкую температуру кипения). Согласно классификации растворы подразделяют на идеальные, предельно разбавленные и реальные. В идеальных растворах взаимодействия между молекулами одного вида и молекулами разных видов одинаковы и их смешение не приводит к изменению объема Δ V см = 0 и не сопровождается тепловым эффектом Δ H см = 0. Если компоненты раствора имеют молекулы близкого состава с одинаковой полярностью, или содержание одного из компонентов настолько мало, что взаимодействиями между молекулами разного вида можно пренебречь, то свойства такого раствора близки к свойствам идеального раствора, такой раствор называют предельно разбавленным. Идеальные растворы подчиняются закону Рауля, согласно которому парциальное давление пара компонента над раствором p 1 равно произведению давления пара чистого компонента Парциальным давлением компонента в газовой смеси называется давление, которое бы он создавал, если бы занимал весь объем смеси. Согласно закону Дальтона давление в любой газовой смеси, в том числе, давление пара над раствором летучих компонентов равно сумме парциальных давлений компонентов и, соответственно, общее давление пара над раствором Таким образом, зависимость давления пара над идеальным раствором двух жидких летучих компонентов от состава раствора имеет вид прямой линии. В случае реальных растворов межмолекулярные взаимодействия могут приводить как к положительным, так и к отрицательным отклонениям от закона Рауля и, соответственно, отклонению уравнения р = f (X) от линейной зависимости. Экспериментально установлено, что состав пара над раствором в общем случае не совпадает с составом раствора, находящегося в равновесии с паром. Пар обогащен более летучим компонентом. Составы совпадают, если давления насыщенного пара над чистыми компонентами одинаковы Различие в составах раствора и равновесного с ним пара лежит в основе перегонки – процесса разделения жидкой смеси на компоненты. Различают: а) простую перегонку, б) фракционную перегонку. Простая перегонка – процесс нагревания смеси жидкостей с отводом образующегося пара и последующей его конденсацией. Образуются две смеси, одна из них содержит больше компонента А, вторая – компонента В. Способ эффективен только при значительной разнице температур кипения чистых растворителей. Фракционная перегонка заключается в многократном повторении процессов испарения и конденсации: 1) нагревание исходной жидкой смеси до кипения для получения некоторого количества пара определенного состава; 2) отделение и конденсация полученного пара; 3) нагревание конденсата для получения пара нового состава, обогащенного легколетучим компонентом. Процесс повторяют до тех пор, когда конденсат и перегоняемый раствор будут представлять чистые компоненты. Для изучения фазовых равновесий жидкость – пар используют диаграммы состояния или фазовые диаграммы, представляющие собой зависимости состав – свойство. График зависимости давления пара от состава при постоянной температуре приведен на рисунке 4.2.
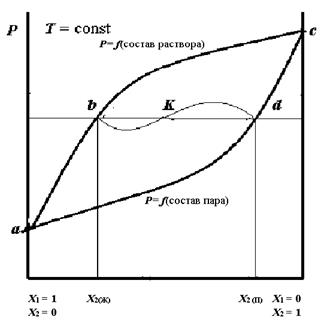
Рисунок. 4.2 – Диаграмма равновесия жидкость – пар при T = const
Верхняя кривая (abc) показывает зависимость давления пара Р от состава раствора, нижняя (adc) – зависимость давления пара Р от состава пара. В области, расположенной выше кривой abc, устойчива жидкая фаза. Область, заключенная между этими кривыми, является гетерогенной: пар находится в равновесии с жидкостью. Смесь, фигуративная точка которой К находится в этой области, распадается на две равновесные фазы – жидкую состава Х 2(Ж) и пар состава Х 2(П). Часто при исследовании равновесия системы жидкость – пар удобно строить диаграмму в координатах температура кипения Т – состав (при Р = const). Вид такой диаграммы представлен на рисунке 4.3. Точки a и b соответствуют температуре кипения чистых компонентов А и В. Так как более летучий компонент имеет более низкую температуру кипения, то точка b на этой диаграмме лежит ниже точки a, в отличие от диаграммы на рисунке 4.2.
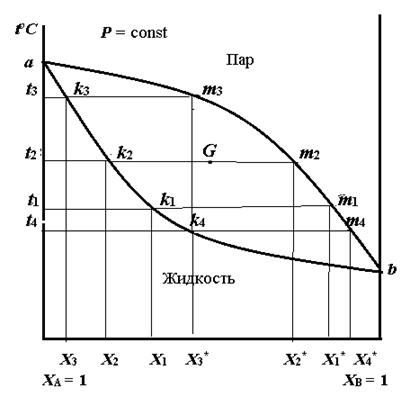
Рисунок 4.3 – Диаграмма равновесия жидкость – пар при p = const
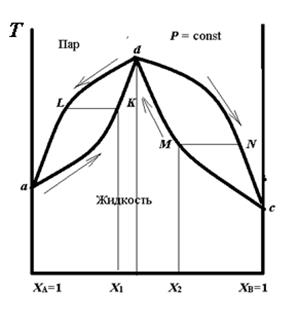
Кривая a.. k.. b показывает состав раствора при заданной температуре кипения, а кривая a.. m.. b – состав равновесного с ним пара при заданной температуре кипения раствора. Выше кривой a.. p.. c находится область пара, а ниже кривой a.. k.. c – жидкая фаза. Любая фигуративная точка в этих полях соответствует составу одной фазы. Между этими кривыми расположена гетерогенная область сосуществования жидкости и равновесного с ним пара. Состав этих фаз определяется координатами точек, лежащих на пересечении изотермы, проходящей через фигуративную точку системы, с кривыми пара и жидкости. Например, система, характеризуемая точкой G, состоит из двух равновесных фаз, состав которых определяется точками k 2 и m 2. Точка k 2 , лежащая на кривой жидкости, характеризует состав жидкости (Х 2), а точка m 2, лежащая на кривой пара, – состав пара (Х 2*). Для определения масс сосуществующих фаз графически используется правило рычага (см. раздел 4.1). При помощи такой фазовой диаграммы можно также объяснить фракционную перегонку. Возьмем для примера раствор состава Х 1. Если нагревать этот раствор, то он закипит при температуре t 1 (точка k 1). Пар, равновесный с этим раствором, имеет состав Х1* (точка m 1). Из рисунка 4.3 видно, что пар обогащен более летучим (с меньшей Тк) компонентом B. После испарения части раствора состав его изменится: он станет богаче менее летучим компонентом A и будет иметь состав Х 2. Раствор такого состава кипит при более высокой температуре t 2 (точка k 2). При кипении этого раствора равновесный с ним пар имеет состав Х 2* (точка m 2), а раствор еще более обогащается компонентом A. Поэтому температура кипения его продолжает повышаться. В результате в остатке будет содержаться чистый компонент A, кипящий при постоянной температуре (точка a). Если пар, например состава Х 3*, сконденсировать, то образующийся раствор закипит при температуре t 4 (точка k 4). При этом образуется пар, обогащенный более летучим компонентом и имеющий состав Х 4* (точка m 4). Если сконденсировать этот пар, то это будет почти чистый растворитель. Продолжая процесс конденсации и испарения, можно получить такой пар, который будет содержать чистый компонент B. Следовательно, при перегонке состав раствора меняется в направлении от точки k 1 к точке a, а состав пара, наоборот – от точки m 1 к точке b. Таким образом, путем фракционной перегонки можно получить из смеси два чистых компонента. Рассмотренные графики иллюстрируют первый закон Коновалова: пар, находящийся в равновесии с жидкостью, богаче тем компонентом, прибавление которого к жидкости повышает давление пара над раствором (или снижают температуру кипения). Для реальных растворов наблюдаются положительные или отрицательные отклонения от закона Рауля и на кривых зависимости Т = f (состав) и р = f (состав) могут наблюдаться максимумы и минимумы. Вид кривой Т = f (состав) при положительных отклонениях от закона Рауля показан на рисунке 4.4, который иллюстрирует второй закон Коновалова: в точках максимальной температуры кипения состав раствора совпадает с составом равновесного с ним пара; максимум на кривой Т= f (состав) соответствует минимуму на кривой р = f (состав). Смесь, в которой составы раствора и пара совпадают при температуре кипения (точка d) и которую невозможно разделить на два составляющих компонента, называется азеотропной. При фракционной перегонке смеси, соответствующей фигуративной точке K состава Х 1, в итоге будут получаться чистый компонент A и азеотропная смесь d. Аналогично, при фракционной перегонке смеси M состава Х 2 будет образовываться чистый компонент B и азеотропная смесь. Таким образом, законы Коновалова лежат в основе способа разделения жидких смесей методом перегонки.
Рисунок 4.4 – Зависимость температуры кипения от состава с азеотропом в минимуме давления пара над раствором
Лабораторная работа №5.
|
||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 128; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.247.24 (0.01 с.) |

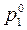 и его мольной доли в растворе
и его мольной доли в растворе 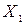 :
: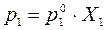 (4.2)
(4.2)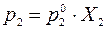 (4.3)
(4.3)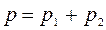 (4.4)
(4.4)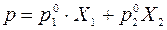 (4.5)
(4.5)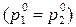 ..
..