
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выполнения работ в лаборатории физической химииСодержание книги
Поиск на нашем сайте 1. При подготовке к выполнению лабораторной работы ее содержание должно быть законспектировано в рабочем журнале. В конспекте следует отразить название и цель работы, записать задания, краткое содержание, последовательность выполнения этапов эксперимента, формулы, необходимые для расчета, и таблицы, в которые следует вносить результаты измерения по мере проведения работы. 2. Все значения физических величин следует выражать в системе СИ. 3. Перед началом работы необходимо получить у преподавателя допуск к ее выполнению. 4. Лабораторную посуду и дополнительное оборудование, необходимое для проведения измерений, получают в препараторской у инженера лаборатории. 4. При выполнении работы результаты измерений необходимо сразу вписывать в подготовленные таблицы в рабочем журнале. 5. По завершению выполнения работы необходимо вернуть в препараторскую посуду, сдать рабочее место и подписать у преподавателя результаты эксперимента. 6. Защита работы проводится на занятии в соответствии с графиком проведения лабораторных работ или во время коллоквиумов. Защита включает проверку знаний теоретического раздела работы, методики ее выполнения и расчетов, выводов по результатам эксперимента. Число баллов, полученное при защите, проставляется преподавателем в лабораторном журнале студента. Обработка экспериментальных данных
При проведении работы в лаборатории физической химии особенное внимание нужно уделять ведению рабочего журнала и правильной записи экспериментальных данных. Все экспериментальные данные записываются непосредственно в рабочий журнал. Полученные данные записывают в таблицу, составленную перед выполнением работы. Это дает возможность заранее предвидеть, какие данные, необходимые для расчета, нужно взять из справочников. Необходимо следить за тем, чтобы числа, вносимые в таблицу, соответствовали точности измерения и давались с соответствующим количеством значащих цифр. Для этого нужно знать цену деления приборов, используемых в работе (бюретки, весы, электроизмерительные приборы и т.д.), правила расчета приближенных величин и теорию ошибок измерения. Все расчеты выполняют в рабочем журнале: записывают формулу, затем подставляют в нее численные значения и приводят результаты вычисления. Графики, диаграммы и т.п. вклеивают в рабочий журнал. В конце работы следует сделать выводы по результатам проведенных исследований; если возможно рассчитать погрешность, которая характеризует правильность результата определения. Абсолютная погрешность представляет собой разность между найденным значением х и истинным (действительным) значением а и имеет размерность измеряемых величин: Δабс . = х – а.
Относительная погрешность – это отношение абсолютной погрешности к истинной величине: Δотн. = (х – a) . 100/ a, %.
Построение графиков
Так как графическое рассмотрение изучаемых процессов является важным методом исследования, то необходимо научиться правильно строить графики. Графики дают возможность: – вывести математическую формулу, описывающую исследуемый процесс; – элиминировать случайные ошибки опыта; – определить методами графического интерполирования или экстраполирования некоторые величины, которые нельзя найти непосредственно из опыта; – позволяют обнаружить наличие максимумов, минимумов, перегибов, характеризующих особенности процесса; – определить важные термодинамические функции и физико-химические постоянные. При построении графиков учитывают следующие общие положения: 1) Графики строят на миллиметровой бумаге размером не более тетрадного листа и приводят название изображенной графической зависимости. 2) Начало осей ординат располагают в левом нижнем углу миллиметровки. 3) При построении кривой y = f (x) значение функции y откладывают на оси ординат, а значение переменной х – на оси абсцисс, указывают их единицы измерения. 4) Масштаб выбирают так, чтобы координаты любой точки графика можно было легко и быстро определить. При выборе учитывают ошибки измерения и соотношение координат. Масштаб характеризует число мм, приходящихся на единицу измерения. Как правило, соотношение координат не должно резко отличаться друг от друга, чтобы график не получился очень растянутым, или, наоборот, с очень большой кривизной. Однако лучше, если график несколько вытянут по оси ординат. Это дает возможность определить значение функции y с большей точностью. 5) Нужно стремиться к тому, чтобы все поле чертежа было полностью использовано. Если значения x или y велики по абсолютной величине и далеки от нулевого значения, то за начало координат можно принять величину, которая несколько меньше самых малых значений x и y. 6) Никогда не следует откладывать на осях координат значения величин, полученные непосредственно из опыта или расчета. Достаточно отложить на осях ряд целых чисел, характеризующих масштаб. 7) В результате измерений или расчетов могут получиться очень большие или, наоборот, очень маленькие цифры. В этом случае на оси координат откладывают значения, содержащие не более 3-х значащих цифр, а обозначение координаты приводят с соответствующим множителем. Например: число 2000 представляют в виде 2,0∙103, тогда на оси у откладывают значение 2,0, а обозначение координаты указывают в виде у ∙10–3. 8) Графики должны быть построены не только правильно, но и аккуратно. Если график строится на основании экспериментальных данных, то обязательно наносят все экспериментальные точки. Благодаря случайным ошибкам экспериментальные точки могут показывать некоторый разброс. Тем не менее, проводимые через них кривые должны быть плавными. Никогда не нужно соединять точки так, чтобы образовывалась ломаная линия. Кривую следует проводить возможно близко ко всем экспериментальным точкам. При этом необходимо, чтобы сумма отклонений всех точек, лежащих с одной стороны кривой, была равна сумме отклонений всех точек, лежащих с другой стороны кривой. Экспериментальные данные (xi, y i ) часто отражают линейную зависимость вида у = ах + b. Чтобы правильно провести прямую линию, равноудаленную от всех точек (xi, y i ), следует сначала рассчитать коэффициенты a и b. Расчет проводят методом наименьших квадратов, используя результаты измерений (xi, y i ), например, в программе Exel. Записывают уравнение у = ах + b, подставив численные значения a и b. Для проведения прямой линии достаточно указать координаты двух точек, принадлежащих этой прямой. Для этого в полученное уравнение подставляют любое произвольное значение x 1 из области экспериментальных данных и рассчитывают соответствующее значение y 1 (точка 1), затем для другого произвольного значения x 2 – значение y 2 (точка 2).. Рассчитанные координаты двух точек наносят на график и через них проводят прямую линию, которая оптимально отражает линейную зависимость. Отклонение каждой экспериментальной точки от этой прямой будет минимальным. Метод графического экстраполирования. Графическая экстраполяция обычно проводится в случае линейной зависимости y = f (x). Прямую линию, описывающуюся уравнением y = ax + b, получают из результатов эксперимента по координатам не менее четырех значений переменных. Продолжив прямую линию до пересечения с осью ординат, определяют значение b как отрезок, который отсекает прямая на оси ординат (y = b при x = 0). Рассмотрим пример: для раствора сильного электролита необходимо найти значение эквивалентной электропроводности при бесконечном разведении l ¥. Для этого экспериментально изучают зависимость l = f (Ö с). Эта зависимость, как видно из уравнения l = l ¥ – а Ö с, описывается прямой линией. При Ö с ® 0, l ® l ¥. Поэтому, если через полученные экспериментальные точки провести прямую линию и продолжить ее до пересечения с осью ординат (экстраполировать на ось ординат), то отрезок, отсекаемый на ординате, равен l ¥. Метод графического интерполирования заключается в нахождении искомой величины, лежащей между двумя известными значениями переменных и функции. Если известны значения Ö с 1 и Ö с 3 и соответствующие им значения l 1 и l 3, а также значение Ö с 2, то из графика можно найти промежуточное значение l 2. Графическое интерполирование можно проводить и в случае нелинейной зависимости.
СтроениЕ молекул. РЕФРАКЦИЯ строение молекул определяет многие как физические, так и химические свойства. Каждая молекула характеризуется индивидуальным расположением положительно заряженных ядер и отрицательно заряженных электронов в молекуле, которому соответствует минимальная энергия. Центры тяжести положительных и отрицательных зарядов совпадают в неполярных молекулах и не совпадают в полярных молекулах. Электрическийдипольный моментµ является характеристикой полярности молекул: где l – расстояние между центрами тяжести положительного и отрицательного зарядов; е – заряд частицы. Единица измерения дипольного момента – 1 дебай (1D = 3,3∙10–30 Кл∙м). В случае совпадения центров тяжести положительного и отрицательного зарядов m = 0. Под воздействием внешнего статического электрического поля в молекуле происходит смещение центров тяжести зарядов, в результате чего молекула приобретает индуцированный дипольный момент. Величина индуцированного (наведенного) дипольного момента m инд. пропорциональна напряженности поля Е: где a – коэффициент пропорциональности, называемый поляризуемостью. Смещение атомов, электронов, ориентация полярных молекул во внешнем электрическом поле называется поляризацией. Поляризуемость характеризует способность молекулы к поляризации и зависит от природы молекулы и направленности электрического поля. Результат воздействия слабого электрического поля на молекулу представляет собой совокупность двух эффектов: – смещения электронов с частичной деформацией молекулярных орбиталей (для полярных и неполярных молекул); – поворота молекулы в целом (только для полярных молекул). Соответственно поляризуемость молекулы складывается из индукционной (электронной) и ориентационной поляризуемости: Ориентационная поляризуемость связана с постоянным дипольным моментом молекулы: где к – постоянная Больцмана, Т – абсолютная температура. Влияние температуры на a ор проявляется в дезориентирующем действии теплового движения молекул. С увеличением температуры ориентационная поляризуемость уменьшается. Индукционная поляризуемость a инд. не зависит от температуры. Поляризуемость совокупности молекул, образующих 1 моль вещества называется молярной поляризацией РМ:
Уравнение Дебая связывает между собой молярную поляризацию, поляризуемость и дипольный момент; где N – число Авогадро. Зависимость молярной поляризации диэлектрика от диэлектрической проницаемости выражает уравнение Клаузиуса-Моссоти:
где ԑ – диэлектрическая проницаемость, М – молярная масса вещества, r – плотность, VM – молярный объем. Комбинирование уравнений (1.6) и (1.7) дает возможность опытным путем определить дипольный момент молекул в газах и жидкостях:
Зависимость (1.8) представляет собой уравнение прямой линии в координатах РМ = f (1/ Т), тангенс угла наклона которой равен (4 p m 2 N)/9 к. Определив экспериментально ԑ и r при разных температурах и рассчитав значения Р М графически находят m. В электромагнитном поле высокой частоты (в том числе в области видимого света) постоянный диполь молекулы не успевает ориентироваться за время одного колебания (~10–15 с), поэтому ориентационная поляризация отсутствует РМ ор = 0 и проявляется только электронная поляризацияРМ = Р М инд .. В этом случае Р Минд . определяется изменением состояния молекулярных орбиталей под действием электромагнитного поля. Величина РМ инд. – важная молекулярная постоянная, ее называют молекулярной рефракцией и обозначают R М = РМ инд. Для неполярных молекул: РМ = R М, для полярных молекул R М, как и РМ, имеет размерность объема и характеризует объем молекул, содержащихся в одном моле вещества. Молекулярная рефракция R М (иногда ее называют молярной рефракцией) практически не зависит от температуры и агрегатного состояния вещества. Из электромагнитной теории света Максвелла известно, что для длин волн, сильно удаленных от области их поглощения молекулами вещества, справедливо равенство n 2 = ԑ, где n – показатель преломления света для определенных длин волн. Тогда уравнение (1.7) преобразуется в уравнение
Уравнение (1.10) называют уравнением Лоренц-Лоренца по именам профессоров Лейденского университета Г.А. Лоренца и Военной школы в Копенгагене Л.В. Лоренца. Молекулярная рефракция связывает показатель преломления вещества с электронной поляризуемостью составляющих его частиц. Как и показатель преломления n молекулярная рефракция R М характеризует способность вещества преломлять свет, однако отличается тем, что практически не зависит от плотности, температуры и агрегатного состояния вещества. Важнейшее свойство рефракции, позволяющее использовать ее для определения строения молекул – аддитивность. Это означает, что молекулярные рефракции соединений могут быть представлены как сумма рефракций составных частей молекулы: атомов, атомных групп и химических связей. Аддитивность рефракций широко применяется как простой и надежный способ проверки правильности предполагаемого строения молекулы. Для этого необходимо рассчитать по правилу аддитивности теоретическое значение рефракции для каждой возможной структуры и сравнить его с рефракцией данного вещества, найденной опытным путем. Для определения экспериментального значения R М практически необходимо найти лишь величины n и r в уравнении (1.10). Совпадение значений R М, полученных опытным и теоретическим путем свидетельствует о правильности предположенной структурной формулы соединения. Лабораторная работа № 1.
|
||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 202; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

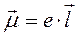 , (1.1)
, (1.1)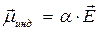 , (1.2)
, (1.2)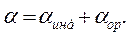 (1.3)
(1.3)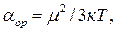 (1.4)
(1.4)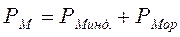 (1.5)
(1.5) (1.6)
(1.6)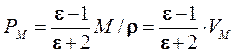 , (1.7)
, (1.7)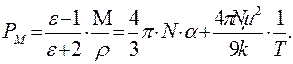 (1.8)
(1.8)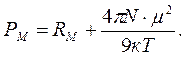 (1.9)
(1.9)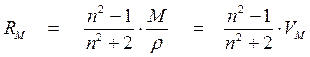 . (1.10)
. (1.10)


