
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторный практикум. Часть 1Содержание книги
Поиск на нашем сайте
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИя РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования «РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМ. А.Н. КОСЫГИНА (ТЕХНОЛОГИИ. ДИЗАЙН. ИСКУССТВО)» (ФГБОУ ВО «РГУ им. А.Н. Косыгина»)
Для направления подготовки 18.03.01 Химическая технология ФИЗИЧЕСКАЯ ХИМИЯ. ЛАБОРАТОРНЫЙ ПРАКТИКУМ. Часть 1
Учебно-методическое пособие
Составители: Кильдеева Н.Р., проф., д.х.н., Гридина Н.Н., доц., к.т.н.
Москва РГУ им. А.Н. Косыгина, 2019 УДК 544(072) К 39
К 39 ФИЗИЧЕСКАЯ ХИМИЯ. ЛАБОРАТОРНЫЙ ПРАКТИКУМ. Часть 1: учебно-методическое пособие./Сост. Кильдеева Н.Р., Гридина Н.Н.,– М.: РГУ им. А.Н. Косыгина, 2019. – 44 с.
Рецензенты:
Сафонов В.В. – д-р техн. наук, проф., ФГБОУ ВО «РГУ им. А.Н. Косыгина»; Платова Т.Е. – канд. хим. наук, доц., ФГБОУ ВО «РГУ им. А.Н. Косыгина»
В лабораторном практикуме (часть 1) приведены подробные руководства для выполнения лабораторных работ и кратко рассмотрены теоретические вопросы по разделам курса физической химии: строение молекул, термохимия, химическое и фазовое равновесия, которые студенты бакалавриата изучают в 4-ом семестре. Даны рекомендации по оформлению лабораторных работ, обработке и представлению полученных результатов. Пособие предназначенодляобучающихся по направлениюподготовки 18.03.01 Химическая технология всех форм обучения и будет использовано при изучении дисциплины «Физическая химия». .
УДК 544(072)
Подготовлено к печати на кафедре химии и технологии полимерных материалов и нанокомпозитов
Печатается в авторской редакции.
© Кильдеева Н.Р., Гридина Н.Н., 2019
содержание ВВЕДЕНИЕ…………………………………………………………………………..4 1. СТРОЕНИЕ МОЛЕКУЛ. РЕФРАКЦИЯ………………………………………8 Лабораторная работа № 1.Определение рефракции и структурной формулы вещества………………………………………………………………….10 2. ТЕРМОХИМИЯ………………………………………………………………. 14 Лабораторная работа № 2. Определение интегральной теплоты растворения соли (безводной и кристаллогидрата) и расчет теплоты гидратации…………………………………………………………………………..19 3. ХИМИЧЕСКОЕ РАВНОВЕСИЕ……………………………………………….23 Лабораторная работа № 3. Определение константы равновесия реакции взаимодействия салициловой кислоты с хлоридом железа в водном растворе……………………………………………………………………………..24 4. ФАЗОВЫЕ РАВНОВЕСИЯ В МНОГОКОМПОНЕНТНЫХ ЖИДКИХ СИСТЕМАХ ………………………………………………………………………..30 4.1. Гетерогенные жидкие системы………………………………………...30 Лабораторная работа № 4. Изучение взаимной растворимости жидкостей и фазового равновесия в двухкомпонентной системе…………………………...33 4.2. Свойства растворов жидких летучих компонентов. Перегонка……..35 Лабораторная работа № 5. Перегонка бинарных смесей полностью смешивающихся жидкостей……………………………………………………….39 ЛИТЕРАТУРА……………………………………………………………………...43
ВвеДение
Настоящее учебно-методическое пособие (часть 1) содержит указания к выполнению лабораторных работ по физической химии, которые студенты, обучающиеся по направлениюподготовки 18.03.01 Химическая технология, выполняют в 4-ом семестре. Материалы лабораторного практикума 5-го семестра изложены во 2-й части пособия. Описанию лабораторной работы предшествует краткий теоретический материал, позволяющий понять цели работы и правильно интерпретировать полученные экспериментальные данные. Материал каждой лабораторной работы содержит цель работы, задание к ее выполнению, описание основных материалов и лабораторного оборудования, таблицы для записи результатов измерений и расчетных величин, последовательность и основные приемы выполнения работы, ссылки на методы расчета и обработки экспериментальных данных. Лабораторные работы выполняются по маршрутам согласно графику, составляемому на первом вводном занятии. Одновременно одинаковую лабораторную работу могут выполнять два студента, однако все записи результатов измерений и последующие расчеты каждый студент делает в своем рабочем журнале. После выполнения лабораторной работы на специально отведенном занятии проводится ее защита. При защите работы учитывается своевременность и аккуратность проведения эксперимента, знание методики выполнения работы, соответствие полученных результатов справочным данным физико-химических величин, правильность расчетов и построения графиков, знание теоретического материала соответствующего раздела курса.
Правила Построение графиков
Так как графическое рассмотрение изучаемых процессов является важным методом исследования, то необходимо научиться правильно строить графики. Графики дают возможность: – вывести математическую формулу, описывающую исследуемый процесс; – элиминировать случайные ошибки опыта; – определить методами графического интерполирования или экстраполирования некоторые величины, которые нельзя найти непосредственно из опыта; – позволяют обнаружить наличие максимумов, минимумов, перегибов, характеризующих особенности процесса; – определить важные термодинамические функции и физико-химические постоянные. При построении графиков учитывают следующие общие положения: 1) Графики строят на миллиметровой бумаге размером не более тетрадного листа и приводят название изображенной графической зависимости. 2) Начало осей ординат располагают в левом нижнем углу миллиметровки. 3) При построении кривой y = f (x) значение функции y откладывают на оси ординат, а значение переменной х – на оси абсцисс, указывают их единицы измерения. 4) Масштаб выбирают так, чтобы координаты любой точки графика можно было легко и быстро определить. При выборе учитывают ошибки измерения и соотношение координат. Масштаб характеризует число мм, приходящихся на единицу измерения. Как правило, соотношение координат не должно резко отличаться друг от друга, чтобы график не получился очень растянутым, или, наоборот, с очень большой кривизной. Однако лучше, если график несколько вытянут по оси ординат. Это дает возможность определить значение функции y с большей точностью. 5) Нужно стремиться к тому, чтобы все поле чертежа было полностью использовано. Если значения x или y велики по абсолютной величине и далеки от нулевого значения, то за начало координат можно принять величину, которая несколько меньше самых малых значений x и y. 6) Никогда не следует откладывать на осях координат значения величин, полученные непосредственно из опыта или расчета. Достаточно отложить на осях ряд целых чисел, характеризующих масштаб. 7) В результате измерений или расчетов могут получиться очень большие или, наоборот, очень маленькие цифры. В этом случае на оси координат откладывают значения, содержащие не более 3-х значащих цифр, а обозначение координаты приводят с соответствующим множителем. Например: число 2000 представляют в виде 2,0∙103, тогда на оси у откладывают значение 2,0, а обозначение координаты указывают в виде у ∙10–3. 8) Графики должны быть построены не только правильно, но и аккуратно. Если график строится на основании экспериментальных данных, то обязательно наносят все экспериментальные точки. Благодаря случайным ошибкам экспериментальные точки могут показывать некоторый разброс. Тем не менее, проводимые через них кривые должны быть плавными. Никогда не нужно соединять точки так, чтобы образовывалась ломаная линия. Кривую следует проводить возможно близко ко всем экспериментальным точкам. При этом необходимо, чтобы сумма отклонений всех точек, лежащих с одной стороны кривой, была равна сумме отклонений всех точек, лежащих с другой стороны кривой. Экспериментальные данные (xi, y i ) часто отражают линейную зависимость вида у = ах + b. Чтобы правильно провести прямую линию, равноудаленную от всех точек (xi, y i ), следует сначала рассчитать коэффициенты a и b. Расчет проводят методом наименьших квадратов, используя результаты измерений (xi, y i ), например, в программе Exel. Записывают уравнение у = ах + b, подставив численные значения a и b. Для проведения прямой линии достаточно указать координаты двух точек, принадлежащих этой прямой. Для этого в полученное уравнение подставляют любое произвольное значение x 1 из области экспериментальных данных и рассчитывают соответствующее значение y 1 (точка 1), затем для другого произвольного значения x 2 – значение y 2 (точка 2).. Рассчитанные координаты двух точек наносят на график и через них проводят прямую линию, которая оптимально отражает линейную зависимость. Отклонение каждой экспериментальной точки от этой прямой будет минимальным. Метод графического экстраполирования. Графическая экстраполяция обычно проводится в случае линейной зависимости y = f (x). Прямую линию, описывающуюся уравнением y = ax + b, получают из результатов эксперимента по координатам не менее четырех значений переменных. Продолжив прямую линию до пересечения с осью ординат, определяют значение b как отрезок, который отсекает прямая на оси ординат (y = b при x = 0). Рассмотрим пример: для раствора сильного электролита необходимо найти значение эквивалентной электропроводности при бесконечном разведении l ¥. Для этого экспериментально изучают зависимость l = f (Ö с). Эта зависимость, как видно из уравнения l = l ¥ – а Ö с, описывается прямой линией. При Ö с ® 0, l ® l ¥. Поэтому, если через полученные экспериментальные точки провести прямую линию и продолжить ее до пересечения с осью ординат (экстраполировать на ось ординат), то отрезок, отсекаемый на ординате, равен l ¥. Метод графического интерполирования заключается в нахождении искомой величины, лежащей между двумя известными значениями переменных и функции. Если известны значения Ö с 1 и Ö с 3 и соответствующие им значения l 1 и l 3, а также значение Ö с 2, то из графика можно найти промежуточное значение l 2. Графическое интерполирование можно проводить и в случае нелинейной зависимости.
СтроениЕ молекул. РЕФРАКЦИЯ строение молекул определяет многие как физические, так и химические свойства. Каждая молекула характеризуется индивидуальным расположением положительно заряженных ядер и отрицательно заряженных электронов в молекуле, которому соответствует минимальная энергия. Центры тяжести положительных и отрицательных зарядов совпадают в неполярных молекулах и не совпадают в полярных молекулах. Электрическийдипольный моментµ является характеристикой полярности молекул: где l – расстояние между центрами тяжести положительного и отрицательного зарядов; е – заряд частицы. Единица измерения дипольного момента – 1 дебай (1D = 3,3∙10–30 Кл∙м). В случае совпадения центров тяжести положительного и отрицательного зарядов m = 0. Под воздействием внешнего статического электрического поля в молекуле происходит смещение центров тяжести зарядов, в результате чего молекула приобретает индуцированный дипольный момент. Величина индуцированного (наведенного) дипольного момента m инд. пропорциональна напряженности поля Е: где a – коэффициент пропорциональности, называемый поляризуемостью. Смещение атомов, электронов, ориентация полярных молекул во внешнем электрическом поле называется поляризацией. Поляризуемость характеризует способность молекулы к поляризации и зависит от природы молекулы и направленности электрического поля. Результат воздействия слабого электрического поля на молекулу представляет собой совокупность двух эффектов: – смещения электронов с частичной деформацией молекулярных орбиталей (для полярных и неполярных молекул); – поворота молекулы в целом (только для полярных молекул). Соответственно поляризуемость молекулы складывается из индукционной (электронной) и ориентационной поляризуемости: Ориентационная поляризуемость связана с постоянным дипольным моментом молекулы: где к – постоянная Больцмана, Т – абсолютная температура. Влияние температуры на a ор проявляется в дезориентирующем действии теплового движения молекул. С увеличением температуры ориентационная поляризуемость уменьшается. Индукционная поляризуемость a инд. не зависит от температуры. Поляризуемость совокупности молекул, образующих 1 моль вещества называется молярной поляризацией РМ:
Уравнение Дебая связывает между собой молярную поляризацию, поляризуемость и дипольный момент; где N – число Авогадро. Зависимость молярной поляризации диэлектрика от диэлектрической проницаемости выражает уравнение Клаузиуса-Моссоти:
где ԑ – диэлектрическая проницаемость, М – молярная масса вещества, r – плотность, VM – молярный объем. Комбинирование уравнений (1.6) и (1.7) дает возможность опытным путем определить дипольный момент молекул в газах и жидкостях:
Зависимость (1.8) представляет собой уравнение прямой линии в координатах РМ = f (1/ Т), тангенс угла наклона которой равен (4 p m 2 N)/9 к. Определив экспериментально ԑ и r при разных температурах и рассчитав значения Р М графически находят m. В электромагнитном поле высокой частоты (в том числе в области видимого света) постоянный диполь молекулы не успевает ориентироваться за время одного колебания (~10–15 с), поэтому ориентационная поляризация отсутствует РМ ор = 0 и проявляется только электронная поляризацияРМ = Р М инд .. В этом случае Р Минд . определяется изменением состояния молекулярных орбиталей под действием электромагнитного поля. Величина РМ инд. – важная молекулярная постоянная, ее называют молекулярной рефракцией и обозначают R М = РМ инд. Для неполярных молекул: РМ = R М, для полярных молекул R М, как и РМ, имеет размерность объема и характеризует объем молекул, содержащихся в одном моле вещества. Молекулярная рефракция R М (иногда ее называют молярной рефракцией) практически не зависит от температуры и агрегатного состояния вещества. Из электромагнитной теории света Максвелла известно, что для длин волн, сильно удаленных от области их поглощения молекулами вещества, справедливо равенство n 2 = ԑ, где n – показатель преломления света для определенных длин волн. Тогда уравнение (1.7) преобразуется в уравнение
Уравнение (1.10) называют уравнением Лоренц-Лоренца по именам профессоров Лейденского университета Г.А. Лоренца и Военной школы в Копенгагене Л.В. Лоренца. Молекулярная рефракция связывает показатель преломления вещества с электронной поляризуемостью составляющих его частиц. Как и показатель преломления n молекулярная рефракция R М характеризует способность вещества преломлять свет, однако отличается тем, что практически не зависит от плотности, температуры и агрегатного состояния вещества. Важнейшее свойство рефракции, позволяющее использовать ее для определения строения молекул – аддитивность. Это означает, что молекулярные рефракции соединений могут быть представлены как сумма рефракций составных частей молекулы: атомов, атомных групп и химических связей. Аддитивность рефракций широко применяется как простой и надежный способ проверки правильности предполагаемого строения молекулы. Для этого необходимо рассчитать по правилу аддитивности теоретическое значение рефракции для каждой возможной структуры и сравнить его с рефракцией данного вещества, найденной опытным путем. Для определения экспериментального значения R М практически необходимо найти лишь величины n и r в уравнении (1.10). Совпадение значений R М, полученных опытным и теоретическим путем свидетельствует о правильности предположенной структурной формулы соединения. Лабораторная работа № 1. Порядок проведения работы
Определение показателя преломления вещества. Для определения показателя преломления вещества используется прибор рефрактометр. действие рефрактометра основано на явлении полного внутреннего отражения луча света при прохождении его через ту или иную среду. Основной частью рефрактометра являются две прямоугольные призмы 1 и 2 на рисунке 1.1, выполненные из специального стекла и притертые по диагональным плоскостям. Между призмами помещается капля исследуемой жидкости, которая растекается по поверхностям тонким слоем. С помощью зеркала направляют луч света на грань призмы 1. Луч света проходит через призму 1, затем через тонкий слой исследуемой жидкости, потом через призму 2 и, выходя наружу, попадает в компенсатор, а оттуда – в окуляр. При пользовании дневным светом часть лучей, падающих на границу стекло-жидкость под углом a, меньшим предельного, пройдет через жидкость, призму 2 и окуляр. Часть лучей, падающих под углом a 2, большим предельного, не пройдет в жидкость, а отразится внутри призмы 1 на основании принципа полного внутреннего отражения (угол b 2). Поэтому, меняя положение окуляра, можно видеть либо светлое, либо темное поле, или, наконец, одну половину поля светлую, а другую – темную. Положение границы раздела соответствует углу полного внутреннего отражения и связано с показателем преломления исследуемой жидкости. В окуляре рефрактометра имеется визирная линия в виде трех черточек. Путем изменения положения окуляра нужно добиться, чтобы визирная линия совпала с границей раздела светлого и темного полей, которая должна быть четкой. Показатель преломления определяется с точностью до четвертого знака после запятой. Капля жидкости наносится на поверхность призмы пипеткой. Так как жидкость летуча, то измерение нужно делать быстро. После того, как измерение произведено, аккуратно вытирают поверхность призмы фильтровальной бумагой. Рисунок 1.1 – Схема рефрактометра
Определение плотности жидкости. Сухой и чистый пикнометр с пробкой взвешивают сначала на технических весах, затем на аналитических весах. Наливают в него дистиллированную воду и устанавливают нижний мениск жидкости точно по метке. Пикнометр с водой взвешивают на технических, затем на аналитических весах. Затем воду выливают, пикнометр высушивают и наливают в него исследуемую жидкость, доводят жидкость в пикнометре до метки и проводят взвешивания. Записывают в рабочую тетрадь массу пустого пикнометра m о, массу пикнометра с водой m 1 и массу пикнометра с исследуемой жидкостью m 2.
Для нахождения истинной плотности нужно внести поправку на взвешивание в воздухе. Каждое тело, погруженное в воздух, теряет в своей массе столько, сколько весит вытесненный им воздух. Такое влияние оказывает воздух, как на взвешиваемое тело, так и на уравновешивающие его гирьки. Если бы объемы тела и гирек были одинаковы, то влияние воздуха было бы тоже одинаково и при равных массах весы были бы в равновесии. Однако плотность гирек больше, чем тела, и тело вытесняет больше воздуха, чем гирьки; следовательно, на воздухе тело может быть уравновешено меньшей массой гирек. Чтобы найти истинную массу тела, надо в кажущуюся массу тела, полученную при взвешивании на воздухе (m о, m 1, m 2), внести поправку на массу воздуха, соответствующую разнице объемов тела и гирек. Расчет плотности жидкости ведется по уравнению:
где r возд – плотность воздуха (r возд = 0,0012 г/см3). Для расчета используют результаты взвешивания масс на аналитических весах. Плотность воды r Н 2 О при температуре взвешивания находят в справочнике. Эмпирическую формулу вещества получают у преподавателя. На основании полученных значений n и r по формуле (1.10) рассчитывают величину опытной молярной рефракции R М оп. Составляют и заносят в лабораторный журнал все возможные изомеры соединения данного состава. Из справочника выписывают в лабораторный журнал значения атомных рефракций для атомов, составляющих молекулу вещества. По правилу аддитивности рассчитывают теоретические молярные рефракции R М теор для каждого из возможных изомеров: Полученные в работе данные должны быть представлены в виде табл.1.1.
Таблица 1.1 – Данные для установления структурной формулы вещества
Сопоставляют опытное и теоретические значения R М. Выбирают структурную формулу, для которой R М теор наиболее близко к R М оп. Относительную погрешность определения R М рассчитывают по формуле Δотн. = (R Моп – R Мтеор) . 100 / R Мтеор, %. (1.13) Сделайте выводы по проделанной работе.
Контрольные вопросы 1. Понятия: дипольный момент, поляризация, поляризуемость. 2. Из чего складывается поляризация полярных и неполярных молекул? 3. Поляризация деформации. От чего зависит индуцированный дипольный момент? 4. Поляризация ориентации, зависимость ее от температуры. 5. Уравнение Дебая. Смысл входящих в него величин. 6. Молярная рефракция. 7. Последовательность установления структурной формулы вещества. Термохимия
Термохимия – раздел химической термодинамики, который изучает тепловые эффекты химических реакций, теплоты фазовых переходов, теплоты растворения веществ, разбавления растворов и т.п. Выделение или поглощение теплоты в результате химического превращения или физико-химического процесса есть следствие того, что суммарная энергия веществ в конце процесса отличается от суммарной энергии веществ в исходном состоянии. Экспериментально (калориметрически) измеряемая теплота химического превращения зависит от количеств реагентов и условий проведения опыта. Тепловым эффектом химической реакции называют количество теплоты, которое выделяется или поглощается в результате реакции, при условиях: 1)процесс протекает необратимо при постоянном объеме или давлении; 2) во время реакции не совершается других видов (полезной) работы, кроме работы расширения; 3) исходные вещества и продукты реакции имеют одинаковую температуру. В основе изучения термохимических процессов лежит первый закон термодинамики, который для бесконечно малых элементарных процессов имеет следующий вид:
или где δ Q – тепло, сообщенное системе; dU – изменение внутренней энергии системы; δ A – работа, совершаемая системой против внешних сил; P – давление, при котором совершается процесс; dV – изменение объема системы. Если тепло сообщено системе при неизменном объеме (V = const, dV = 0, изохорный процесс), то работа против внешнего давления отсутствует и тепловой эффект реакции Следовательно, при V = const вся теплота, подведенная к системе, расходуется на увеличение ее внутренней энергии. Если тепло сообщено системе при постоянном внешнем давлении (P = const, изобарный процесс), то тепловой эффект реакции
где изменение энтальпии системы Следовательно, в изобарном процессе теплота, переданная системе, расходуется на увеличение внутренней энергии ( Δ U) P и на совершение работы против внешнего давления. При этом теплота изобарного процесса равна приращению энтальпии системы во время этого процесса. В качестве основной единицы измерения теплоты в системе СИ установлен джоуль (Дж). Для описания тепловых явлений в химических реакциях принято пользоваться термохимическими уравнениями. Термохимические уравнения записываются с указанием физического состояния вещества: газообразное (г), жидкое (ж), кристаллическое (к) или раствор (р-р); с указанием аллотропной (полиморфной) модификации, а также величины и знака теплового эффекта химической реакции. В случае экзотермических реакций в правой части уравнения записывают количество выделившейся теплоты со знаком «плюс», в случае эндотермических реакций – количество поглощенной теплоты со знаком «минус». Если в уравнении химической реакции указывается не тепловой эффект, а изменение ее энтальпии Например: Са(к) + С(гр) + З/2O2 =СаСОз(к) + 1206,8кДж или Са(к) + С(гр) + З/2O2 =СаСОз(к),
основным законом термохимии является закон Гесса: если из данных исходных веществ можно получить заданные конечные вещества различными путями, то суммарная теплота на одном каком-нибудь пути равна суммарной теплоте процесса на любом другом пути. Таким образом, тепловой эффект химических реакций не зависит от пути перехода, а определяется только начальным и конечным состояниями системы. Закон Гесса незаменим для расчета тех тепловых эффектов, которые нельзя измерить калориметрически. Например, теплоту образования СО (D Н) при реакции С + О2 вследствие течения реакции как с образованием СО, так и СО2 экспериментально определить невозможно. Однако с помощью закона Гесса с использованием легко определяемых калориметрически тепловых эффектов реакций D Н 1, и D Н 2 он может быть рассчитан: С + О2 = СО2, D Н 1 СО + 1/2О2 = СО2, D Н 2 С + 1/2О2 = СО, D Н D Н 1 = D Н + D Н 2 по закону Гесса D Н = D Н 1 – D Н 2 Закон Гесса применим и для определения тепловых эффектов, сопровождающих процессы растворения веществ, разбавления жидкостей. Он используется для расчета тепловых эффектов реакции по стандартным теплотам образования или сгорания веществ, расчета энергии химической связи. Реакции, при которых теплота поглощается (Δ U >0 и Δ H >0) называются эндотермическими, а реакции, протекающие с выделением теплоты (Δ U <0 и Δ H <0) – экзотермическими. Тепловой эффект считают: – положительным D Н > 0 (Q P < 0) для реакций, при которых теплота поглощается (эндотермические); – отрицательным D Н < 0 (Q P > 0), е сли реакция протекает с выделением теплоты (экзотермические). Тепловой эффект, сопровождающий процесс растворения вещества в жидкости называется теплотой растворения. Различают интегральную и дифференциальную теплоту растворения. Интегральной теплотой растворения называют тепловой эффект растворения 1 моля вещества в таком количестве растворителя, чтобы получился раствор концентрации С m. Дифференциальной теплотой растворения – тепловой эффект растворения 1 моля вещества в бесконечно большом количестве раствора концентрации С m. Дифференциальные теплоты определяются расчетным методом, а интегральные – экспериментально. Определение тепловых эффектов химических реакций и физико-химических процессов проводят в специальных приборах калориметрах. Следует различать два способа проведения калориметрического опыта. При одном из них температура пространства, окружающего калориметр, остается в течение всего опыта постоянной (калориметр с изотермической оболочкой). При другом – температура оболочки, окружающей калориметр, в течение опыта меняется так, чтобы в каждый момент времени она была равна температуре калориметра (калориметр с адиабатической оболочкой). Последний способ употребляется в том случае, если исследуемые процессы протекают очень медленно и возможна потеря части теплового эффекта процесса в результате теплообмена калориметра с окружающей средой. Любой калориметрический опыт сводится к определению изменения температуры калориметрической жидкости в результате проходящего в ней химического или физико-химического процесса. Тепловые эффекты рассчитывают, используя экспериментальные данные и известные значения теплоемкости. Теплоемкостью называют количество теплоты, поглощаемой веществом при его нагревании на 1оС (1K). Различают удельную и молярную теплоемкости. Молярная теплоемкость – это количество теплоты, поглощаемой 1 моль вещества при нагревании его на 1оС. Истинную теплоемкость определяют как количество теплоты, поглощаемое при бесконечно малом изменении температуры С = d Q /d Т. В эксперименте определяют среднюю теплоемкость с = D Q / D Т. Если процессы происходят при постоянном давлении или объеме, то D Q Р = – D Н, а D Q V = – D U. Тогда:
С использованием калориметрических данных и приведенных формул рассчитывают значения теплоемкостей и тепловые эффекты химических реакций и физико-химических процессов. Лабораторная работа № 2 Определение интегральной теплоты растворения соли (безводной и кристаллогидрата) и расчет теплоты гидратации
Цель работы: Освоение методики калориметрических измерений и определение теплоты гидратации соли CuSO4. Задание: 1. Освоить методику работы на калориметре. 2. Провести измерение изменения температуры в результате растворения солей и работы нагревателя. 3. Рассчитать теплоемкость калориметрической системы. 4. Рассчитать интегральные теплоты растворения безводной соли и кристаллогидрата в воде. 5. Рассчитать теплоту гидрат
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 155; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.64.245 (0.014 с.) |

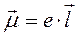 , (1.1)
, (1.1)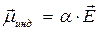 , (1.2)
, (1.2)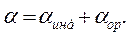 (1.3)
(1.3)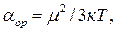 (1.4)
(1.4)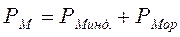 (1.5)
(1.5) (1.6)
(1.6)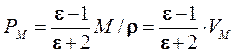 , (1.7)
, (1.7)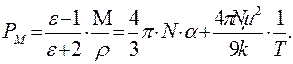 (1.8)
(1.8)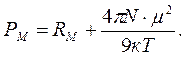 (1.9)
(1.9)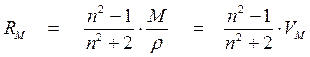 . (1.10)
. (1.10)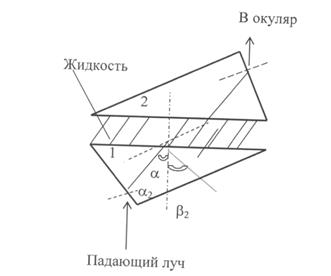
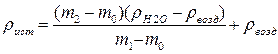 , (1.11)
, (1.11)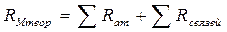 (1.12)
(1.12)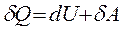 (2.1)
(2.1)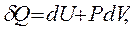 (2.2)
(2.2)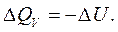 (2.3)
(2.3)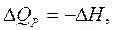 (2.4)
(2.4)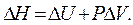
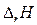 , оно записывается отдельно.
, оно записывается отдельно.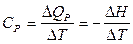 ;
; 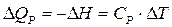 (2.5)
(2.5)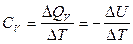 ;
; 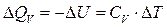 (2.6)
(2.6)


