
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Описание калориметрической установкиСодержание книги
Поиск на нашем сайте
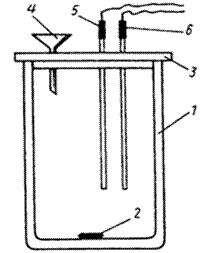
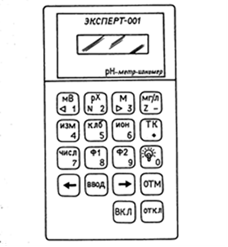
В работе используется калориметрическая установка, которая состоит из калориметрического стакана с магнитной мешалкой и измерительного прибора «ЭКСПЕРТ-001». Схематическое изображение калориметрического стакана приведено на рисунке 2.1, внешний вид прибора – на рисунке 2.2. В стакан 1 помещен сердечник магнитной мешалки 2. Пластмассовая крышка 3, закрывающая стакан, имеет три отверстия: одно – для воронки 4, второе – для датчика температуры 5, позволяющего регистрировать температуру с точностью до сотых долей градуса, третье – для нагревателя 6 с точно известным электросопротивлением. Отверстия в крышке снабжены зажимами, позволяющими надежно закреплять нагреватель и датчик температуры на необходимой высоте. Высота крепления подбирается так, чтобы сердечник магнитной мешалки не задевал за них при работе.
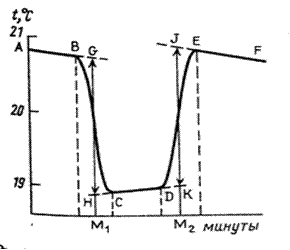
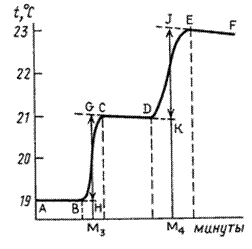
В процессе опыта на экране прибора «ЭКСПЕРТ-001» высвечиваются значения температуры и время, которые записываются в рабочий журнал. Строят график в координатах температура (°С) – время (мин). Примерные графики изменения температуры во времени для эндотермического и экзотермического процессов представлены на рисунках 2.3 и 2.4.
Каждый опыт по определению тепловых эффектов химических реакции начинают с определения температурного хода калориметрической системы. Для этого в калориметрический стакан наливают требуемое для реакции количество реагента (в нашем случае воды) и в течение 5–6 мин записывают его температуру (температурный ход калориметрической системы описывает участок АВ на рисунках 2.3 и 2.4). Если в течение этого времени изменение температуры невелико или температура остается постоянной, начинают основной эксперимент.
Для этого в некоторый момент отсчета времени в жидкость калориметра добавляют второе реагирующее вещество (в нашем случае соль) при постоянном перемешивании. В результате реакции температура калориметрической системы изменяется – см. участок ВС на рис 2.3 и рис. 2.4. После окончания реакции изменение температуры в калориметре прекратится или станет медленным и равномерным (участок С D). Наличие небольшого наклона на графике температурной зависимости в начальном (АВ) и конечном (С D) периодах свидетельствует о том, что во время опыта имеет место теплообмен калориметра с окружающей средой. В расчетах теплообмен учитывается следующим образом. Прямая АВ экстраполируется вправо, прямая С D влево. Интервал времени от В до С делится пополам и через эту точку (M 1(3)) проводится перпендикуляр к оси абсцисс до пересечения его с экстраполированными участками прямых АВ и С D. Величина отрезка Н G соответствует изменению температуры калориметрической системы Δ T 1 только за счет теплового эффекта реакции. Тепловой эффект процесса (например, процесса растворения) может быть рассчитан по формуле где С К – теплоемкость калориметра, т.е. количество теплоты, которое необходимо для нагревания калориметра с его содержимым на 1°. Оно определяется экспериментально сразу после окончания реакции (процесса растворения). Для этого с помощью электрического нагревателя, включенного на заданное время Δ τ, калориметрической системе сообщается точно известное количество теплоты Количество теплоты
где U – напряжение постоянного тока, подаваемого на нагреватель, В; R – электрическое сопротивление нагревателя, Ом; Δ τ – время работы нагревателя, с. Для установки «ЭКСПЕРТ-001» U = 12 В; R = 10 Ом. Тогда теплоемкость калориметра:
Измеренный тепловой эффект следует отнести к 1 моль вещества, для чего его необходимо разделить на число молей (п) того из участников реакции, который находится в недостатке, тогда Лабораторная работа № 2 Определение интегральной теплоты растворения соли (безводной и кристаллогидрата) и расчет теплоты гидратации
Цель работы: Освоение методики калориметрических измерений и определение теплоты гидратации соли CuSO4. Задание: 1. Освоить методику работы на калориметре. 2. Провести измерение изменения температуры в результате растворения солей и работы нагревателя. 3. Рассчитать теплоемкость калориметрической системы. 4. Рассчитать интегральные теплоты растворения безводной соли и кристаллогидрата в воде. 5. Рассчитать теплоту гидратации на основании полученных тепловых эффектов (по закону Гесса).
В настоящей работе в калориметрической установке, описанной выше, определяются энтальпии растворения безводного сульфата меди CuSO4 (Δ H 1):
CuSO4·(к) + aq = CuSO4 (р-р)
и кристаллогидрата сульфата меди CuSO4·5H2O (Δ H 2):
CuSO4·5H2O(к) + aq = CuSO4 (р-р)
На основании экспериментально полученных данных рассчитывается энтальпия образования кристаллогидрата (Δ H) по реакции: CuSO4 (к) + 5H2O(ж) = CuSO4·5H2O(к)
Для этого используют закон Гесса
По закону Гесса D H 1 = D H + D H 2; D H = D H 1 – D H 2.
Интегральные теплоты растворения безводной соли и ее кристаллогидрата рассчитывают, используя экспериментальные значения D Т оп1 и D Т оп2 и значение С к, где D Т оп1 и D Т оп2 – изменение температуры в результате растворения n 1 моль безводной соли и n 2 моль ее кристаллогидрата (соответственно):
Затем по закону Гесса вычисляют теплоту образования кристаллогидрата (гидратации) D H. Порядок проведения работы 1. Определение теплоты растворения безводной соли CuSO 4 и теплоемкости калориметрической системы Взвесьте 3 г безводной соли CuSO4 с точностью до 0,01 г. В калориметрический стакан налейте 130 мл дистиллированной воды, температура которой близка к комнатной. Опустите в калориметрический стакан сердечник магнитной мешалки и включите в розетку 220 В измерительный прибор «ЭКСПЕРТ-001». Нажмите и удерживайте в течение 2с кнопку «ВКЛ» (см. рисунок 2.2) на приборе (при этом начнет светиться его экран). Первая надпись на экране прибора «ЭКСПЕРТ-001» показывает уровень зарядки его собственных аккумуляторов. При напряжении на аккумуляторе менее 30% необходимо его зарядить при помощи сетевого адаптера. Вращая ручку включения магнитной мешалки, добейтесь оптимальной скорости вращения ее сердечника (скорость, когда при вращении мешалки на поверхности воды образуется воронка глубиной ≈ 1–1,5 см). Выберите время работы электрического нагревателя при определении теплоемкости калориметра. Для этого на клавиатуре прибора «ЭКСПЕРТ-001» (рис. 2.2) нажмите кнопку «Ф2» и далее кнопку «ЧИСЛ». Цифровыми кнопками наберите время работы нагревателя (секунды). Рекомендуемое время 200 с. После установки времени нагрева два раза нажмите кнопку «ВВОД». Кнопками «стрелка влево» (←) или «стрелка вправо» (→) выберите режим «ТЕРМОМЕТР». Нажмите кнопку «ИЗМ», и на экране появятся данные работы секундомера, работающего в режиме прямого отсчета времени, и значения температуры в калориметрическом стакане. Результаты измерений времени и температуры заносят в лабораторный журнал в виде таблицы 2.1.
Определите тепловой ход калориметрической установки (участок АВ на рисунках 2.3 и 2.4). Для этого записывайте показания температуры через каждые 30 с в течение 5 мин. Если измерения показывают, что в течение 5 мин температурные изменения невелики, начинайте эксперимент. В определенный момент времени, отметив его (*) в рабочем журнале, откройте крышку калориметрического стакана и всыпьте приготовленную навеску сульфата меди CuSO4. За счет растворения соли происходит быстрое изменение температуры, поэтому записывайте ее значения через возможно малые промежутки времени (10 с). После того как растворение соли закончится, изменение температуры замедлится, и температурный ход снова станет равномерным (участок CD на рисунках 2.3 и 2.4), продолжайте измерения температуры через 30 с еще в течение 5 мин. Не отключая установки, определите теплоемкость калориметрической системы. Для этого нажмите клавишу «Ф2» (рисунок 2.2). На экране прибора появится время, установленное в начале эксперимента для нагрева калориметрической установки. Отметьте это время (*) в рабочем журнале, Секундомер начнет работать в режиме обратного отсчета времени. Записывайте значения температуры в рабочий журнал через каждые 10 с. Продолжайте измерять температуру еще в течение 5 мин через каждые 30 с. Нажмите клавишу «ОТКЛ» на клавиатуре прибора «ЭКСПЕРТ-001».. Таблица 2.1 – Экспериментальные данные t ° С = f (τ)
* Отметить время начала растворения и время включения нагревателя
2. Определение теплоты растворения кристаллогидрата CuSO 4 ·5 H 2 O Взвесьте 6 г CuSO4·5H2O с точностью до 0,01 г. Проведите опыт по определению теплоты растворения кристаллогидрата CuSO4·5H2O так, как это описано выше.
Обработка результатов 1. По результатам температурных измерений постройте графики на отдельных листах миллиметровой бумаги (удобнее формат А4). На оси абсцисс нанесите время в минутах, а на оси ординат – температуру, ° С. 2. Определите по графику изменение температуры Δ T оп калориметрической установки в результате нагрева (отрезок JK). 3. Определите по графику изменение температуры Δ T 1 в результате реакции растворения безводной соли CuSO4. 4. Определите по графику изменение температуры Δ T 2 в результате реакции растворения кристаллогидрата CuSO4·5H2O. 5. Рассчитайте теплоемкость калориметрической системы Ск, используя формулы 2.8 и 2.9. 5. Определите интегральную теплоту растворения – тепловой эффект реакции растворения безводной соли D H 1. 6. Определите тепловой эффект реакции (энтальпию) реакции растворения кристаллогидрата D H 2. 7. Используя полученные результаты, рассчитайте энтальпию реакции образования пентагидрата сульфата меди D H: CuSO4 (к) + 5H2O(ж) = CuSO4·5H2O(к) Сделайте выводы по проделанной работе.
Контрольные вопросы 1. Тепловой эффект реакции, эндо– и экзотермические реакции. 2. Первый закон термодинамики. 3. Закон Гесса и его применение. 4. Что такое теплота гидратации? 5. Понятие теплоемкости. Химическое равновесие
Химическое равновесие – состояние реакционной системы, в которой химическая реакция одновременно протекает в двух противоположных направлениях с одинаковой скоростью, поэтому состав системы остается постоянным, пока не изменятся внешние условия. Математическим выражением законов термодинамики для равновесия химических процессов является закон действующих масс: отношение произведения равновесных концентраций (или парциальных давлений) продуктов реакции, взятых в степенях, равных их стехиометрическим коэффициентам к аналогичному произведению для исходных веществ при данной температуре есть величина постоянная. Таким образом, для реакции вида: а А + b B ↔ c C + d D
где К с и К р – константы равновесия этой реакции при определенной температуре. Константа равновесия химической реакции позволяет знать направление и предел ее возможного протекания. Если для реакционной смеси с определенными значениями парциальных давлений р ’ A, р ’ B, р’ C и р’ D составить выражение
D G = – RT ln(Kp – K ’ p), (3.3)
которое называют уравнение изотермы химической реакции (изотермы Вант-Гоффа при T = const и p = const). С помощью уравнения изотермы (3.3) можно определить химическое сродство различных веществ, т.е. характеризовать их способность вступать во взаимодействие друг с другом. Если известна константа равновесия, то можно легко оценить знак правой части уравнения.
Если реакционная смесь содержит все компоненты в стандартных условиях, т.е. Р ’A = P ’B = P ’C = P ’D = 1атм, тогда ln К ’p = 0. Уравнение изотермы упрощается:
D G о = – RT ln Kp. (3.4)
Стандартное изменение энергии Гиббса D G о широко используется для определения направления химических процессов. Знак перед D G о Т является критерием самопроизвольного протекания химической реакции. Минус указывает возможность протекания реакции в прямом направлении. Если D G о Т больше нуля, т.е. Kp ˂ 1 то данная реакция не может самопроизвольно идти в прямом направлении в стандартных условиях (при указанной температуре). Принципиально возможно только протекание обратной реакции. Система находится в равновесии, если D G о Т = 0. Чем более отрицательна величина изобарно-изотермического потенциала, тем больше константа равновесия и выше выход продуктов реакции. Из уравнений (3.3) и (3.4) получаем уравнение для определения сродства в нестандартных условиях D G = –D G о + RT ln K ’ p . (3.5)
Справедливы аналогичные уравнения –D F о = R Т ln K c (3.6)
D F = –D F о + RT lnK’ c (3.7) где D F и D F o – потенциал Гельмгольца и стандартное сродство (при T = const и V = const). Следует отметить, что если реакция идет без изменения числа молей в газовой фазе, то К р = К с.
Лабораторная работа №3.
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 503; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.87.144 (0.011 с.) |
||||||||||||||||||||||||||||||||||

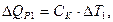 (2.7)
(2.7) 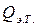 (электрического тока) и измеряется вызванное ею изменение температуры (участок DE на рис. 2.3 и 2.4). После отключения нагрева регистрируется заключительный участок температурной кривой Е F. Величина Δ T оп, соответствующая изменению температуры при нагревании калориметрической системы, получается при обработке участка графика С D Е F с учетом теплообмена калориметра с окружающей средой.
(электрического тока) и измеряется вызванное ею изменение температуры (участок DE на рис. 2.3 и 2.4). После отключения нагрева регистрируется заключительный участок температурной кривой Е F. Величина Δ T оп, соответствующая изменению температуры при нагревании калориметрической системы, получается при обработке участка графика С D Е F с учетом теплообмена калориметра с окружающей средой.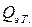 , сообщенное калориметрической системе при нагреве, вычисляется по формуле Джоуля:
, сообщенное калориметрической системе при нагреве, вычисляется по формуле Джоуля: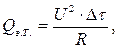 (2.8)
(2.8) 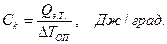 (2.9)
(2.9) 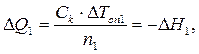 (2.10)
(2.10)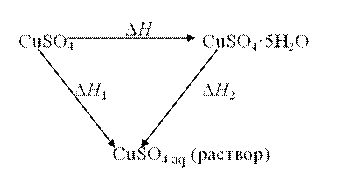

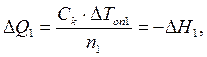
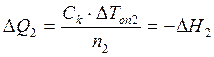 . (2.11)
. (2.11)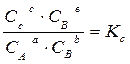 (3.1)
(3.1)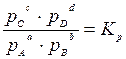 (3.2)
(3.2)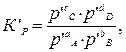 то связь между К р и D G (энергия Гиббса) можно описать уравнением:
то связь между К р и D G (энергия Гиббса) можно описать уравнением:


