
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные допущения при изучении течения газаСодержание книги
Поиск на нашем сайте
В лопаточной машине
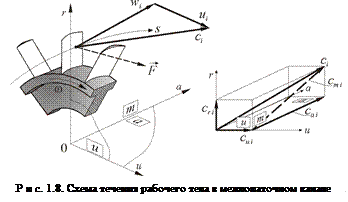
Рассмотрим в общем случае течение некоторого объёма рабочего тела в межлопаточном канале ЛМ (рис. 1.8). Система координат связана с неподвижной осью ЛМ, при этом ось or соответствует оси oz в декартовой системе координат: оси оа и ои - осям ох и оу соответственно. На выделенный объём рабочего тела со стороны лопатки действует сила В общем случае скорость ci является функцией четырёх переменных ci = f (r, u, a, t); проекции объёмной силы (включающей и силу Рабочий процесс в самом общем случае описывается известными уравнениями гидромеханики [9]. В частности, для оценки изменения параметров рабочего тела по всей линии тока используются уравнения движения в форме Эйлера или Лагранжа. Они могут быть получены при рассмотрении равновесия частицы под действием всех объёмных сил (включая и силы инерции). В принятой системе координат (см. рис. 1.8) уравнения движения для несжимаемого газа имеют вид [13]
Уравнения (1.2) очень сложны, и решение их в общем случае затруднительно. В практике расчётов используются упрощенные схемы течения рабочего тела в ЛМ, которые называются моделями ЛМ. Прежде чем приступить к рассмотрению моделей ЛМ, введем некоторые специфические понятия. Условимся называть плоскость, проходящую через оси or и oa, меридиональной, и будем обозначать её “ m ” (см. рис. 1.8, а). Плоскости, проходящие через оси or - oи и oa - ои называются плоскостями вращения “ и ” и осевой “ а ” (см. рис. 1.8, а) соответственно. Нетрудно увидеть (см. рис. 1.8, б), что в плоскости “ и ” расположены проекции с r i и с u i скорости с i, в “ а ” - с u i и с a i, а в “ m ” - с r i и с a i. Часто в плоскости “ m ” выделяют меридиональную составляющую скорости
Рассмотренное разложение скорости с i в плоскостях “ m ”, “ и ” и “ а ” позволяет решать проектировочные задачи, в которых параметры потока определяются сокращённым числом пространственных координат. Например, если принять течение в ЛМ установившимся
|
|||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 115; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.40.171 (0.007 с.) |

 , а мгновенная абсолютная скорость ci на линии тока s является векторной суммой переносной и относительной скоростей, т.е. ` ci = ` wi + ` u i.
, а мгновенная абсолютная скорость ci на линии тока s является векторной суммой переносной и относительной скоростей, т.е. ` ci = ` wi + ` u i.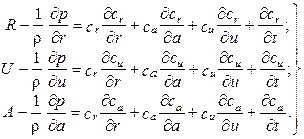 (1.2)
(1.2)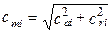 .
.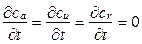 и равномерным
и равномерным 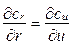 , то течение рабочего тела через ЛМ можно представить как перенос расчётной массы через кольцевое сечение (см. рис. 1.8, а), расположенное в плоскости “ и ”. При этом перенос массы Gi осуществляется со скоростью с a i, а параметры рабочего тела изменяются лишь вдоль оси оа. Для такой схемы течения система уравнений (1.2) значительно упрощается и появляется возможность решения целого ряда практических задач.
, то течение рабочего тела через ЛМ можно представить как перенос расчётной массы через кольцевое сечение (см. рис. 1.8, а), расположенное в плоскости “ и ”. При этом перенос массы Gi осуществляется со скоростью с a i, а параметры рабочего тела изменяются лишь вдоль оси оа. Для такой схемы течения система уравнений (1.2) значительно упрощается и появляется возможность решения целого ряда практических задач.


