
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема. Основы математической статистики в агрономии. Методы статистической обработки результатов исследований.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Основные понятия и задания математической статистики. 2. Анализ вариационных рядов количественной и качественной изменчивости.
Все статистические методы основаны на теории вероятностей – науке, изучающей общие закономерности в массовых случайных явлениях различной природы. Объектам агрономических (биологических) исследований (растения, их группы, урожай и окружающая природная среда) присуще явление изменчивости, то есть отличие друг от друга даже в однородных совокупностях.
Изменчивость – это свойство, присущее всем объектам природы. Ч.Дарвин сказал: «В природе нет двух совершенно одинаковых растительных или животных организмов, то есть они имеют свою изменчивость». Варьирование возникает не только от индивидуальной для каждого биологического объекта наследственности, но и от того, что их формирование протекает в относительно различных условиях внешней среды. Поэтому, в агрономических опытах, даже при самой тщательной работе, урожаи на параллельных делянках или в сосудах всегда получаются разные. Следовательно, при любом исследовании данные опытов будут всегда варьировать в тех или иных пределах. У растений варьирующими признаками являются: высота, вегетативная масса, кустистость, площадь листовой поверхности, показатели структуры колоса (метелки, корзинки и т.д.) – количество и масса зерна с колоса, масса 1000 зерен, натура, стекловидность, содержание белка, клейковины, крахмала, масличность, лузжистость, сахаристость и многие другие. Изменчивость, варьирование признаков создает известную трудность в тех случаях, когда требуется дать общую характеристику определенной варьирующей группе (совокупности) растений, почв и т.п. по отдельным признакам или сравнить две такие группы и найти различие между ними. Очевидно, что не всегда возможно исследовать по тому или иному признаку все особи, всю совокупность. В этом случае прибегают к изучению части её, по которой делают общее заключение. Метод называют выборочным и считают основным при статистическом изучении совокупности.
Число элементов в генеральной совокупности и выборке называют их объёмом. Главная цель выборочного метода – по статистическим показателям малой выборки (средней пробе) наиболее точно охарактеризовать всю совокупность объектов, т.е. генеральную совокупность. Аналогично, при постановке полевых опытов, в которых не более 4-8 одноименных (повторных) делянок и по их урожаям и другим показателям, т.е. по этой малой выборке из общей площади опытного участка, пытаются получить достоверные выводы относительно всего опытного участка, всей генеральной совокупности, которая должна быть охарактеризована возможно более простыми статистическими показателями. Полученные сведения о численной величине изучаемого признака (Х) у каждого члена данной выборочной совокупности называют вариантами и обозначают Х1, Х2, …, Хn. Полученный ряд варьирующих величин можно упорядочить – расположить значения признака (варианты) в порядке возрастания или убывания (ранжирование ряда). Далее можно заметить, что каждое значение признака встречается неодинаковое количество раз – одни редко, другие часто. Числа, которые характеризуют, сколько раз повторяется каждое значение признака у членов данной совокупности, называется частотами признака (f). Сумма всех частот (∑ f) равна объёму выборки, т.е. числу членов ряда – n. В результате такой обработки первичных наблюдений получаем Вариационный ряд, т.е. ряд данных, в которых указаны возможные значения варьирующего признака в порядке их возрастания или убывания и соответствующие им частоты. Этот ряд бывает прерывистым (если значения вариантов целые числа) и непрерывным (если они дробные). Прерывистый ряд – количество растений на 1 м2, зерен в колосе, колосьев, метелок или початков на растении и т.д. Непрерывный – значения вариант выражаются мерами длины, объёма, массы и имеют неограниченное число значений; всё зависит от степени точности для характеристики этого количественного признака. Основные характеристики вариационного ряда: f – частота однородных дат (значений изучаемого показателя - чисел); Х – варианта, значение отдельного признака, показателя; n – численность ряда;
∑ f (X - X)2
S n - 1
S S
ν = (n – 1) – число степеней свободы вариации (число всех измерений изучаемого признака без единицы (число ню).
n - 1 n - 1 Далее рассмотрим и выполним конкретное задание по следующей теме: «Составить вариационный ряд подсчета всходов подсолнечника на 1 м погонном рядка провести его анализ». Подсчет проводится на 1 погонном метре рядка в 10-ти местах по 10 проб (метровок) метров. Исходные данные будем брать из таблицы проведенных в поле подсчетов всходов растений подсолнечника (таблица 1). Таблица 1. Количество всходов подсолнечника на 1 метре рядка, штук
В таком виде ряд подсчетов густоты всходов подсолнечника (n=100) малопригоден для характеристики варьирования густоты. Затем подсчитываем одинаковые числа (начиная от 0 и до 7) и составляем вариационный ряд и частоту однородных дат. => мы группируем значения Х1, Х2…Хnв К групп с интервалом каждой группы i. Таблица 2. Составление и анализ вариационного ряда
Ориентировочно число групп равно √100, из объёма выборки, оно не должно быть менее 5 и болем 20. В нашем случае оно равно 8. Расчеты параметров вариационного ряда n – численность ряда у нас = 100 (10 × 10) или f; (сумма частот равна объёму совокупности ∑f = n = 100; Х × f = ∑f x – всего всходов подсолнечника (насчитали 300 шт.);
å×f×(X- å×f×(X- S2(g2), дисперсия = å×f×(X- S(g), среднее квадратическое отклонение от S – мера разброса отдельных наблюдений (замеров) вокруг среднего значения признака. Чем больше дисперсия или стандартное отклонение, тем больше рассеяны индивидуальные значения признака около средней, т.е. больше изменчивость, и наоборот.
 Выводы Выводы
1. Среднее количество всходов на 1 пог. м. = 3 + 0,128, т.е. при повторных подсчетах оно может колебаться в пределах 2,872-3,128. 2. Густота посевов не выровнена, V значительный (42,7%, более 20%). 3. Точность вычисления (анализа) – удовлетворительная (4,3%). Кривая вариационного ряда близка к синусоиде, т.е. к нормальному распределению. Для справки: если V <10% - варьирование незначительное; если 10%<V<20% - варьирование среднее; если V>20% - варьирование значительное;
Задача: Составить непрерывный вариационный ряд значений замера диаметра корзинки подсолнечника (табл. 3, 4). Замеры диаметра корзинки подсолнечника проводились в фазу спелости (восковая окраска тыльной стороны) в 5-ти местах по 10 растений подряд. Таблица 3. Диаметр корзинки подсолнечника, см
Xmin, наименьший диаметр = 15,5 см. Xmax, наибольший диаметр = 22,4 см. Xmax - Xmin = 6.9»7 cм. Выделяем 7 классов с разницей = 1 см и группируем в них замеры. Таблица 4. Составление и обработка вариационного ряда
C – корректирующий фактор = (åfXv)2/n = 9542/50 = 18202; S2 – дисперсия = (åfX2v –С)/n-1 = (18274-18202)/50-1 = 1,46; S – среднее квадратическое отклонение =
Выводы 1. Средний размер диаметра корзинки подсолнечника составляет 19,1±0,17 см (18,93-19,27). 2. Варьирование вариационного ряда – слабое (V<10%). 3. Точность определения – отличная (<2%).
Лекция №7.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 965; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

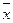 - средняя арифметическая [ (∑f х) / n ];
- средняя арифметическая [ (∑f х) / n ];
 S – среднее квадратическое (стандартное) отклонение [ √ S2 ];
S – среднее квадратическое (стандартное) отклонение [ √ S2 ]; S2 – дисперсия (квадрат стандартного отклонения) [ ];
S2 – дисперсия (квадрат стандартного отклонения) [ ]; V – коэффициент вариации [ × 100% ]»
V – коэффициент вариации [ × 100% ]» S
S  √ n
√ n вычисления [ × 100% ];
вычисления [ × 100% ]; Пояснение. При вычислении Х все величины независимы друг от друга, => их сумма (∑) делится на общее число вариант n (например)
Пояснение. При вычислении Х все величины независимы друг от друга, => их сумма (∑) делится на общее число вариант n (например) 5 – 3 – 4 – 6 – 5 - набор чисел, вариант, их сумма равна 23, а их Х (средняя арифметическая) = 23: 54 = 4,6.
5 – 3 – 4 – 6 – 5 - набор чисел, вариант, их сумма равна 23, а их Х (средняя арифметическая) = 23: 54 = 4,6. (+0,4; -1,6; -0,6; +1,4; 0,4) = 0 сумма отклонений от Х равна 0.
(+0,4; -1,6; -0,6; +1,4; 0,4) = 0 сумма отклонений от Х равна 0.


 Но когда известен ряд наблюдений от Х1 до Хn, то каждое значение ряда (Х) и каждое отклонение (Х–Х) можно легко определить по значению Х и значениям остальных n – 1 вариант ряда. Любое отклонение зависит от величины всех остальных и численно равно их сумме, взятой с противоположным знаком, т.е. ∑ всех отклонений ∑(Х – Х) = 0. => неизвестное нам отклонение должно свести эту сумму к 0. => Отклонение одной любой отдельной варианты как бы лишено свободы вариации и точно определяется варьированием всех остальных вариант, т.е. (n – 1). => Число независимых величин при определении S2 и S, равно не n, a (n – 1).
Но когда известен ряд наблюдений от Х1 до Хn, то каждое значение ряда (Х) и каждое отклонение (Х–Х) можно легко определить по значению Х и значениям остальных n – 1 вариант ряда. Любое отклонение зависит от величины всех остальных и численно равно их сумме, взятой с противоположным знаком, т.е. ∑ всех отклонений ∑(Х – Х) = 0. => неизвестное нам отклонение должно свести эту сумму к 0. => Отклонение одной любой отдельной варианты как бы лишено свободы вариации и точно определяется варьированием всех остальных вариант, т.е. (n – 1). => Число независимых величин при определении S2 и S, равно не n, a (n – 1).
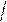 ∑ f (X - X) ∑ f (X - X)2
∑ f (X - X) ∑ f (X - X)2 
 S2 =
S2 =  (Х – х)
(отклонение от средней)
(Х – х)
(отклонение от средней)
 f(X-x)
f(X-x)
 (X-x)2
(X-x)2
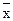 )2
)2

 Х - среднее арифметическое значение = (åfх)/n = 300/100 = 3.
Х - среднее арифметическое значение = (åfх)/n = 300/100 = 3.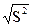 =
= 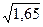 = ± 1,28;
= ± 1,28; S – стандартное отклонение – показатель, характеризующий наиболее вероятную среднюю ошибку отдельного, единичного наблюдения, взятого из данной совокупности. В пределах одного значения (± 1 S) укладывается ≈ 2/3 всех наблюдений, или 68,3% всех вариант, т.е. основная часть изучаемого ряда величин. => S называется основным отклонением вариационного ряда. => возможны отклонения от X, превосходящие (± 1 S), но их вероятность по мере удаления отклонений от (± 1 S) все время уменьшается. Вероятность встретить варианту, отклоняющуюся от Х на величину > (± 3S) ≈ 0,3%.
S – стандартное отклонение – показатель, характеризующий наиболее вероятную среднюю ошибку отдельного, единичного наблюдения, взятого из данной совокупности. В пределах одного значения (± 1 S) укладывается ≈ 2/3 всех наблюдений, или 68,3% всех вариант, т.е. основная часть изучаемого ряда величин. => S называется основным отклонением вариационного ряда. => возможны отклонения от X, превосходящие (± 1 S), но их вероятность по мере удаления отклонений от (± 1 S) все время уменьшается. Вероятность встретить варианту, отклоняющуюся от Х на величину > (± 3S) ≈ 0,3%. V, коэффициент вариации = S ×100 = (1,28/3)×100 = 42,7%;
V, коэффициент вариации = S ×100 = (1,28/3)×100 = 42,7%; x
x
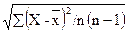 =
= 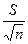 =
= 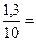 0,13.
0,13.

 Sx – ошибка выборочной средней (выборки) – это мера отклонения выборочной средней Х от средней всей (генеральной) совокупности µ. Sх возникает вследствие неполной репрезентативности (представительности) выборочной совокупности. Величина Sх зависит от степени изменчивости изучаемого признака и от объёма выборки. Чем больше S, тем больше Sх, и чем больше число измерений n, тем меньше Sx.
Sx – ошибка выборочной средней (выборки) – это мера отклонения выборочной средней Х от средней всей (генеральной) совокупности µ. Sх возникает вследствие неполной репрезентативности (представительности) выборочной совокупности. Величина Sх зависит от степени изменчивости изучаемого признака и от объёма выборки. Чем больше S, тем больше Sх, и чем больше число измерений n, тем меньше Sx.

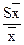 × 100%. В нашем случае Sx =
× 100%. В нашем случае Sx = 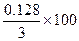 = 4.3%.
= 4.3%.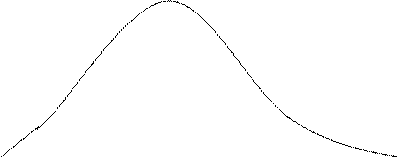
 если 4 < Sx% < 5% - удовлетворительная точность вычисления;
если 4 < Sx% < 5% - удовлетворительная точность вычисления; если Sx% > 5 % - низкая точность вычисления.
если Sx% > 5 % - низкая точность вычисления. 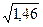 = ±1,2 см;
= ±1,2 см;
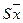 – ошибка средней = S/Ön = 1,2/Ö50 = ±0,17 см;
– ошибка средней = S/Ön = 1,2/Ö50 = ±0,17 см;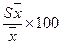 = 0,9%.
= 0,9%.


