
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кривая водоизмещения и грузовой размер. Грузовая шкала
Для определения осадки по водоизмещению или, наоборот, водоизмещения по осадке используют кривую водоизмещения V (z). Чтобы ее построить, необходимо вычислить интеграл с переменным верхним пределом:
где хн и хк — абсциссы точек пересечения ватерлиний с линиями форштевня и ахтерштевня соответственно при осадке z. Вид кривой V (z) представлен на рис. 6, где также изображены кривые V в (z) и М (z) = ρ V в (z). Кривая V в (z) характеризует объемное водоизмещение с учетом выступающих частей (обшивки, килей и т. п.), а М (z) — водоизмещение с учетом плотности воды (масса). Кривая М (z) называется грузовым размером. Плотность воды зависит от района плавания, а также от температуры воды (т. е. от сезона), поэтому иногда строят ряд кривых М (z) для различных ρ.
Рис. 6. Кривая водоизмещения и грузовой размер для обычного судна. МОДУЛЬ 3. ЭЛЕМЕНТЫ ТЕОРЕТИЧЕСКОГО ЧЕРТЕЖА Элементы площади ватерлинии Чтобы определить V, хс, zс,необходимо знать площади ватерлиний S и абсциссы хf центров тяжести этих площадей. Для расчета остойчивости следует вычислить моменты инерции площадей ватерлиний относительно координатных осей Ох, Оу и оси ff, проходящей через центр тяжести площади ватерлинии. Вначале найдем элементы площади ватерлинии для судна, сидящего прямо и на ровный киль. Выделим элементарную площадь, (рис. 1) длиной dx и шириной 2у: dS = 2 ydx, тогда
Рис. 1. К определению элементов площади симметричной ватерлинии.
Абсцисса центра тяжести площади ватерлинии равна х f = My / S, (2) где My — статический момент площади ватерлинии относительно оси Оу. Для определения Му выпишем сначала выражение для статического момента элементарной площади dS: dMy = xdS = x 2 ydx, откуда
Теперь получим формулы для определения осевых моментов инерции площади ватерлинии относительно главных центральных осей Найдем момент инерции dIx элементарной площади dS,для чего воспользуемся известной из теоретической механики формулой для момента инерции площади прямоугольника относительно главнойцентральной оси:
Тогда
Момент инерции площади ватерлинии S относительно оси ff равен
В процессе эксплуатации судно может плавать с начальным креном, когда ватерлиния несимметрична относительно ДП. Чтобы рассчитать для данного случая площадь, статические моменты, моменты инерции и другие элементы введем правые уп и левые ул ординаты (рис. 2).
Рис. 2. К определению элементов площади несимметричной ватерлинии
Согласно рис. 2 выражение для площади элемента с учетом того, что уп отрицательна, можно записать в виде dS = yndx — ул dx =(уп - ул) dx, а площадь ватерлинии как
Тогда
Для несимметричной ватерлинии статический момент площади относительно оси Ох не равен нулю. Статический момент для правой элементарной площадки равен
для левой –
суммарный -
Тогда формула для полного статического момента запишется в виде
Центр тяжести F площади ватерлинии будет находиться от ДП на расстоянии
Для моментов инерции элементарной площадки можно записать следующие выражения
Следовательно, моменты инерции относительно осей координат будут равны
Но в дальнейшем в расчетах нам потребуются моменты инерции относительно осей, проходящих через центр тяжести F площади ватерлинии. Они определяются по формулам
Формула (10) позволяет вычислить также статический момент погруженного объема М xz несимметричного судна относительно ДП, а затем и ординату ЦВ ус. Статический момент может быть представлен как интегральная сумма статических моментов элементарных объемов
или с учетом (10)
Ордината ЦВ
|
||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 152; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.28.70 (0.012 с.) |
 ,
,
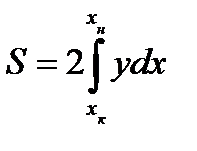 . (1)
. (1)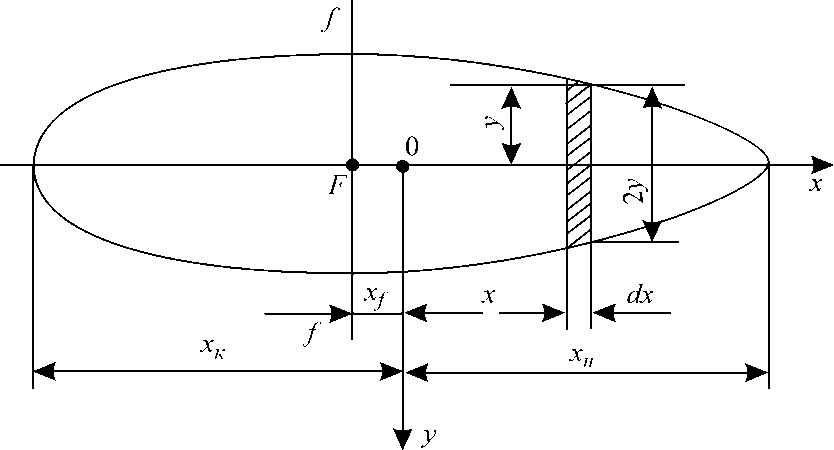
 . (3)
. (3)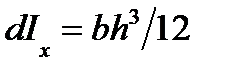 , где b = dx, h = 2 y, т. e.
, где b = dx, h = 2 y, т. e. .
.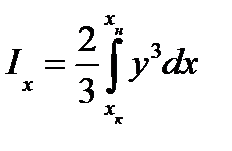 . (4)
. (4)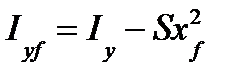 , (5)
, (5)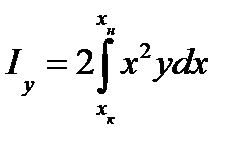 , (6) так как элементарный момент инерции площади dS равен
, (6) так как элементарный момент инерции площади dS равен 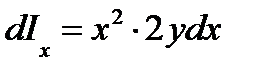 ; Sx 2 f — переносный момент инерции.
; Sx 2 f — переносный момент инерции.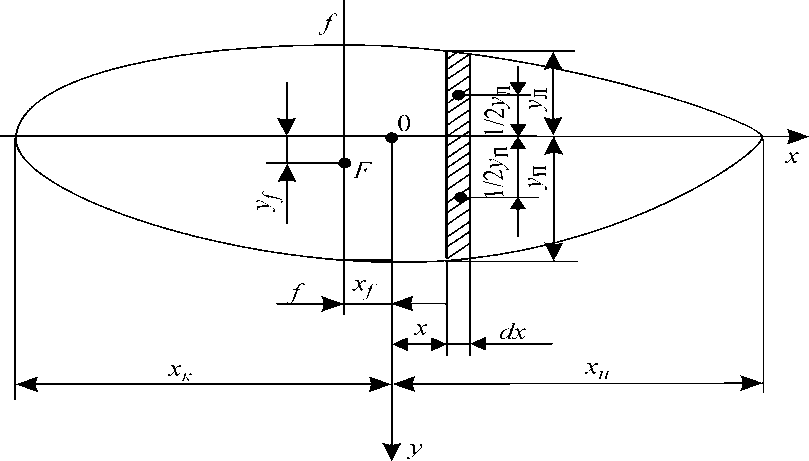
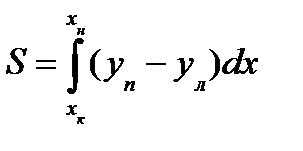 . (7) Аналогично для статического момента площади S относительно оси Оу получим
. (7) Аналогично для статического момента площади S относительно оси Оу получим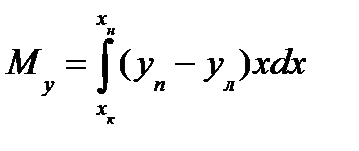 (8)
(8)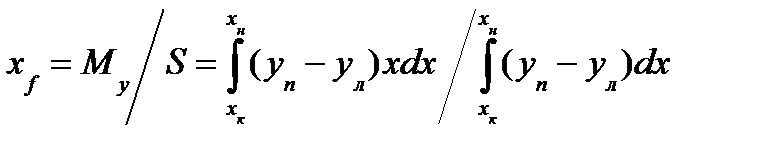 (9)
(9)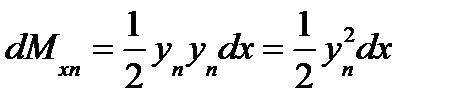 ,
,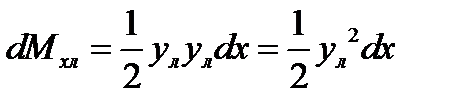 ,
,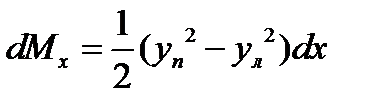
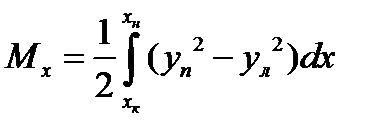 .(10)
.(10) . (11)
. (11) ;
;  .
. ; (12)
; (12)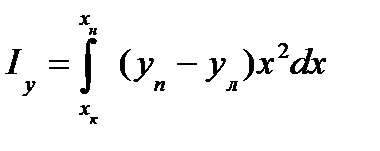 . (13)
. (13)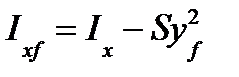 ;
;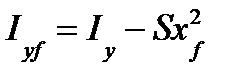 . (14)
. (14)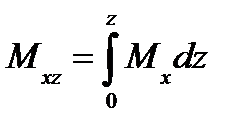 ,
,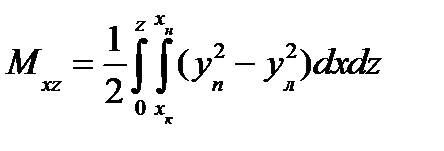 .
.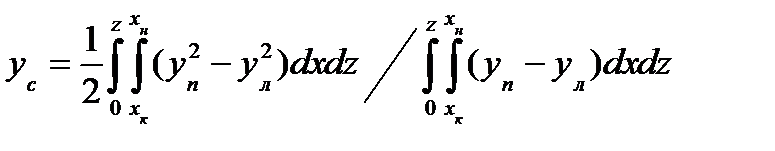 . (15)
. (15)


