
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модуль 1. Мореходные качества и Теоретический чертеж суднаСтр 1 из 13Следующая ⇒
СТАТИКА КОРАБЛЯ (модули) д.т.н., профессор Борисов Р.В.
Санкт- Петербург 2012 г. МОДУЛЬ 1.МОРЕХОДНЫЕ КАЧЕСТВА И ТЕОРЕТИЧЕСКИЙ ЧЕРТЕЖ СУДНА Основные мореходные качества корабля Теория корабля -это наука о его мореходных качествах. Знание мореходных качеств необходимо при проектировании судна с целью обеспечения его безаварийной эксплуатации. К мореходным качествам судна относятся: плавучесть, остойчивость, непотопляемость,ходкость, умеренность качки и управляемость. Рассмотрим определения этих мореходных качеств. Плавучесть-способность корабля плавать в определенном положении относительно поверхности воды. Остойчивость-способность корабля сохранять равновесие при внешнем воздействии или при его отсутствии. Непотопляемость- способность судна при затоплении одного или нескольких отсеков оставаться на плаву и сохранять в определенной мере плавучесть и остойчивость. Ходкость-способность корабля двигаться с заданной скоростью при эффективном использовании мощности силовой установки. Умеренность качки–является следующим мореходным качеством. Качка-это колебательное движение корабля на поверхности воды. Качка очень вредное явление. Понятие умеренность качки включает малость и плавность наклонений корабля. Управляемость-способность корабля удерживать заданное направление движения. Статика корабля представляет собой раздел теории корабля в который входят: плавучесть, остойчивость и непотопляемость. Ходкость,качка и управляемость входят в раздел, который называется динамикой корабля. Все мореходные качества судна (корабля) зависят от размеров и формы корпуса. Поэтому прежде чем приступить к расчетам мореходных качеств необходимо описать форму корпуса судна. Теоретический чертеж судна Теоретический чертеж судна изображает его поверхность без наружной обшивки в виде трех проекций: бок, корпус, полуширота. Рассмотрим построение этих проекций. Для построения теоретического чертежа используют 3 взаимно-перпендикулярные координатные плоскости: диаметральную плоскость (ДП), плоскость мидель-шпангоута (ПМШ), и основную плоскость(ОП). Диаметральная плоскость рассекает судно вдоль и является продольной плоскостью симметрии. Плоскость мидель-шпангоута разрезает судно поперек перпендикулярно диаметральной плоскости на середине расчетной длины судна. Основная плоскость является перпендикулярной к диаметральной плоскости и плоскости мидель-шпангоута. Она проходит через точку пересечения этих плоскостей с поверхностью судна в его днищевой части (рис.1).
Для построения теоретического чертежа проводят дополнительные плоскости, параллельные трем основным. Сечения поверхности судна плоскостями, параллельными диаметральной плоскости называются батоксами. Сечения поверхности судна плоскостями, параллельными плоскости мидель-шпангоута, называются шпангоутами. Сечения поверхности судна плоскостями, параллельными основной плоскости называются ватерлиниями. Таким образом, судно имеет три вида сечений: батоксы, шпангоуты и ватерлинии. Проекции всех этих сечений на диаметральную плоскость образуют проекцию бок. На этой проекции батоксы изображаются в виде кривых линий. Шпангоуты и ватерлинии изображаются в виде прямых линий и образуют сетку (рис. 2).
Рис.1. Координатные плоскости
Проекции всех сечений на плоскость мидель-шпангоута образуют проекцию корпус. На этой проекции шпангоуты изображаются в виде кривых линий. Батоксы и ватерлинии изображаются в виде прямых. Обычно изображают половины шпангоутов: носовые ветви-справа, кормовые ветви шпангоутов-слева. Мидель-шпангоут изображают на оба борта. Проекции всех сечений на основную плоскость образуют проекцию полуширота. На этой проекции ватерлинии изображаются в виде кривых линий. Шпангоуты и батоксы изображаются в виде прямых и образуют сетку. На теоретическом чертеже изображают равноотстоящие батоксы, ватерлинии и шпангоуты. Количество батоксов обычно бывает от 2 до 6, количество ватерлиний5-15,шпаноутов 11-21. За нулевойбатокс принимается сама диаметральная плоскость. Кроме указанных сечений на теоретическом чертеже изображают линии верхней палубы, надстроек, форштевня, ахтерштевня. Ватерлиния, по которую судно плавает во время эксплуатации, называется главной или грузовой ватерлинией (ГВЛ). Для судов, которые не перевозят груз,эта ватерлиния называется конструктивной (КВЛ)
Корпус
Полуширота
Рис.2 Теоретический чертеж судна
Системы координат При расчетах статики вводят две прямоугольные системы координат с началом в точке O. Первая система Oxyz связана с судном. Другая называется полусвязаннойсистемой (рис.3). В связанной системе координат плоскость xOz -диаметральная, плоскость xOy -основная плоскость, yOz -плоскость мидель шпангоута. Ось Ox -линия пересечения диаметральной плоскости и основной, направлена в нос судна, ось Oy -линия пересечения основной плоскости и плоскости мидель-шпангоутанаправлена на правый борт, ось Oz –линия пересечения диаметральной плоскости и плоскости мидель-шпангоута направлена вертикально вверх. В полусвязанной системе коодинат ось Формулы перехода от связанной системы к полусвязанной системе координат имеют вид:
В формулы (1) y входит со своим знаком: для точек правого борта-положительным, левого-отрицательным. Корпус судна характеризуется главными размерениями, их соотношениями и коэффициен-тами полноты.
Рис.3. Системы координат и главные измерения судна: а -связанная; б -полусвязанная система
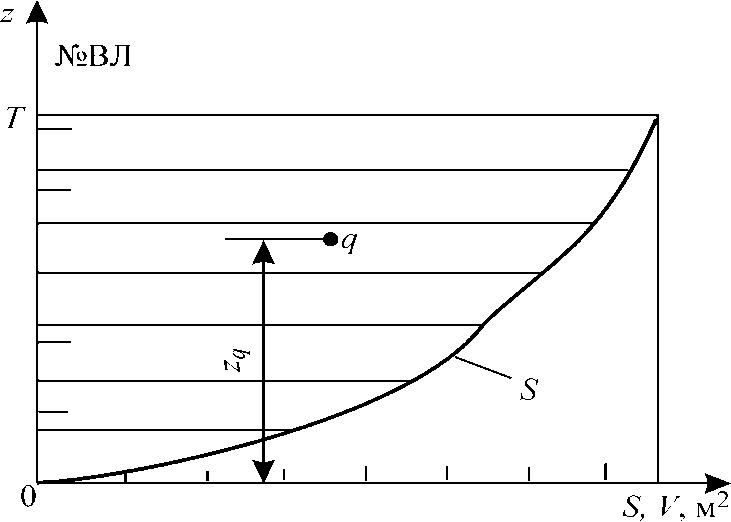
Главные размерения судна Главными размерениями судна является его длина, ширина, высота борта, осадка. Рассмотрим определения основных величин: Длина наибольшая Lmax -это расстояние по горизонтали между крайними точками форштевня и ахтерштевня; Длина между перендикулярами L -это расстояние между точками пересечения КВЛ с теоретической линией форштевня и осью баллера руля для одновинтовых судов или с теоретической линией ахтерштевня для двухвинтовых судов. Эта длина является расчетной и делится на 20 (10) равных частей (в зависимости от количества шпангоутов)-теоретических шпаций. Шпация-это расстояние между шпангоутами. Длина по КВЛ L квл-расстояние между точками пересечения КВЛ с форштевнем и ахтерштевнем; для двухвинтовых судов онасовпадает с длиной между перпендикулярами. Ширина наибольшая Bmax -расстояние, измеренное перпендикулярно диаметральной плоскости в наиболее широкой части корпуса без учета выступающих частей. Ширина по КВЛ Bизмеряется на КВЛ в месте максимальной ширины судна (обычно на мидель-шпангоуте).Эта величина является расчетной. Высота борта H - вертикальное расстояниеот основной плоскости до линии палубы у борта (рис. 3) Осадка судна T -вертикальное расстояние от основной плоскости до КВЛ. Эта величина является расчетной. Расчетные значения L, B, T служат для разбивки сетки теоретического чертежа. Строевая по ватерлиниям Строевая по ватерлиниям - это кривая, показывающая изменение площадей ватерлиний по высоте корпуса судна. Построить ее можно следующим образом (рис.4):
Рис.4.Строевая по ватерлиниям.
Строевая по ватерлиниям характеризует распределение объемного водоизмещения по высоте.
Основные свойства строевой по ватерлиниям:
Тогда
Строевая по шпангоутам Строевая по шпангоутам - это кривая, которая показывает изменениеплощадей погруженных частей шпангоутов по длине судна. Строят ее следующим образом (рис. 5): 1) на оси Ох отмечают точки, характеризующие в определенном масштабе положение шпангоутов; 2) из этих точек восстанавливают перпендикуляры к оси Ох и на них откладывают заранее вычисленные площади шпангоутов Ω i; 3) концы перпендикуляров соединяют плавной линией.
Рис. 5. Строевая по шпангоутам.
Строевая по шпангоутам характеризует распределение объемного водоизмещения по длине судна, что очень важно знать в процессе проектирования. Свойства строевой по шпангоутам: 1. Площадь Q, которая ограничена сверху кривой, а снизу осью абсцисс, представляет в некотором масштабе объемное водоизмещение V. Действительно,
2. Коэффициент полноты площади строевой по шпангоутам равен коэф-фициенту продольной полноты судна. Из рис. 5. следует, что
где Ωм — площадь мидель - шпангоута. 3. Абсцисса центра тяжести площади строевой по шпангоутам xq представляет собой в масштабе длин абсциссу ЦВ судна хс. Статический момент площади Q равен
Тогда
Элементы площади ватерлинии Чтобы определить V, хс, zс,необходимо знать площади ватерлиний S и абсциссы хf центров тяжести этих площадей. Для расчета остойчивости следует вычислить моменты инерции площадей ватерлиний относительно координатных осей Ох, Оу и оси ff, проходящей через центр тяжести площади ватерлинии.
Вначале найдем элементы площади ватерлинии для судна, сидящего прямо и на ровный киль. Выделим элементарную площадь, (рис. 1) длиной dx и шириной 2у: dS = 2 ydx, тогда
Рис. 1. К определению элементов площади симметричной ватерлинии.
Абсцисса центра тяжести площади ватерлинии равна х f = My / S, (2) где My — статический момент площади ватерлинии относительно оси Оу. Для определения Му выпишем сначала выражение для статического момента элементарной площади dS: dMy = xdS = x 2 ydx, откуда
Теперь получим формулы для определения осевых моментов инерции площади ватерлинии относительно главных центральных осей Найдем момент инерции dIx элементарной площади dS,для чего воспользуемся известной из теоретической механики формулой для момента инерции площади прямоугольника относительно главнойцентральной оси:
Тогда
Момент инерции площади ватерлинии S относительно оси ff равен
В процессе эксплуатации судно может плавать с начальным креном, когда ватерлиния несимметрична относительно ДП. Чтобы рассчитать для данного случая площадь, статические моменты, моменты инерции и другие элементы введем правые уп и левые ул ординаты (рис. 2).
Рис. 2. К определению элементов площади несимметричной ватерлинии
Согласно рис. 2 выражение для площади элемента с учетом того, что уп отрицательна, можно записать в виде dS = yndx — ул dx =(уп - ул) dx, а площадь ватерлинии как
Тогда
Для несимметричной ватерлинии статический момент площади относительно оси Ох не равен нулю. Статический момент для правой элементарной площадки равен
для левой –
суммарный -
Тогда формула для полного статического момента запишется в виде
Центр тяжести F площади ватерлинии будет находиться от ДП на расстоянии
Для моментов инерции элементарной площадки можно записать следующие выражения
Следовательно, моменты инерции относительно осей координат будут равны
Но в дальнейшем в расчетах нам потребуются моменты инерции относительно осей, проходящих через центр тяжести F площади ватерлинии. Они определяются по формулам
Формула (10) позволяет вычислить также статический момент погруженного объема М xz несимметричного судна относительно ДП, а затем и ординату ЦВ ус. Статический момент может быть представлен как интегральная сумма статических моментов элементарных объемов
или с учетом (10)
Ордината ЦВ
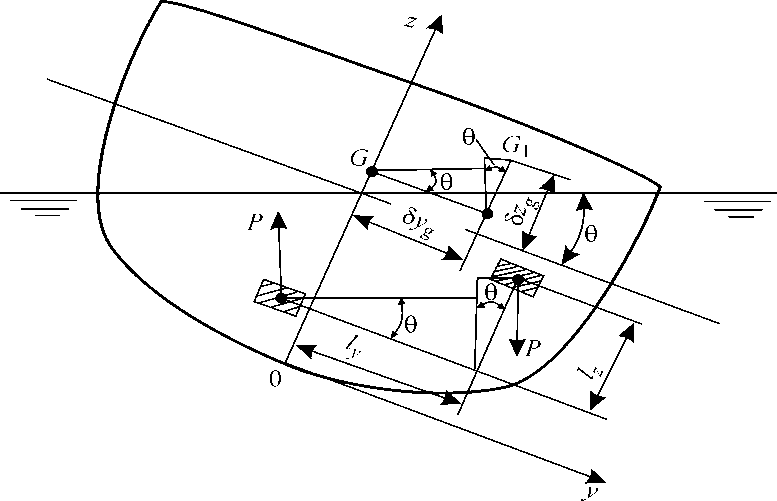
МОДУЛЬ 4. ПРАКТИЧЕСКИЕ ВОПРОСЫ ПЛАВУЧЕСТИ Перенос груза Пусть на судне некоторый груз P массой m перенесен так, что ЦТ этого груза переместился из точки с координатами x 0, y 0, z 0 в точку с координатами x 1, y 1, z 1. Тогда масса всего судна не изменится, но изменится положение его ЦТ. Разлагая фактическое перемещение ЦТ груза на три взаимно перпендикулярных перемещения, параллельные координатным осям, рассматриваем продольное перемещение l x = x 1 — x 0 поперечное перемещение ly = y 1 — y 0 и вертикальное перемещение lz = z 1 — z 0 (рис. 1). Перемещение ЦТ судна можно найти с помощью теоремы теоретической механики о статических моментах, согласно которой
Благодаря этому перемещению появятся две дополнительные пары сил. Одна из них будет действовать в ДП, вызывая дифферент. Плечо ее будет равно дифферентующий
кренящий
Рис. 1. Кренящая пара сил при переносе груза
Подставляя в эти формулы выражения (1), получим
Будем считать, что углы наклонения судна достаточно малы, так что
Согласно условиям равновесия действие этих моментов уравновесится действием восстанавливающих моментов. Определим последние по метацентрическим формулам остойчивости:
Отсюда угол дифферента, возникающий вследствие переноса груза, равен
а угол крена
Выражения для метацентрических высот, измененные из-за влияния переноса груза, будут следующие:
где поправки к метацентрическим высотам оказываются одинаковыми;
Для большинства судов продольная метацентрическая высота намного больше поперечной. Поэтому в практических расчетах поправкой
Если груз переносится в нос, то Подвешенный груз Пусть груз p с ЦТ в точке B подвешен на судне или жестко связанном с ним устройстве в некоторой точке A (рис. 2, а). Если груз закреплен в этой точке, то при наклонении судна он перемещаться не сможет и дополнительного влияния на остойчивость не оказывает, этот груз просто войдет в нагрузку масс судна с координатами точки B как ЦТ. Если же груз не закреплен или в процессе наклонения судна освобождается, то ЦТ груза переместится в сторону наклонения, в точку B 1. Линия подвеса, разумеется, останется вертикальной и перпендикулярной поверхности воды, а угол между линиями подвеса до наклонения и после него будет равен углу наклонения судна, например углу крена
где l — длина подвеса;
Действие на судно дополнительного кренящего момента можно трактовать как уменьшение восстанавливающего момента
Величина pl / D — поправка к метацентрической высоте, обусловленная перемещением груза:
Эта поправка всегда отрицательна; значит, влияние подвешенного груза можно рассматривать так же, как перемещение его ЦТ наверх, в точку подвеса, в результате чего аппликата ЦТ судна изменяется на
Эта величина не зависит от угла наклонения, следовательно, она будет одной и той же при малых и больших углах крена, при наклонениях в поперечной и продольной плоскостя х. Таким образом, поправка к продольной метацентрической высоте равна
При выводе всех этих формул на величину груза p никаких ограничений не накладывалось. Поэтому они справедливы как для малого, так и для большого подвешенного груза.
Перекатывающийся груз Пусть на судне находится твердый груз, который при наклонении в некоторой плоскости перекатывается так, что его ЦТ перемещается в той же плоскости по кривой из точки B в точку B 1 (рис. 2, б). Для каждого угла наклонения сила тяжести груза действует по нормали к кривой BB 1 в соответствующей точке, вэта нормаль перпендикулярна плоскости действующей ватерлинии. Если точка B отвечает положению равновесия судна, а точка B 1 — наклонению на малый угол
Рис.2. К оценке влияния на остойчивость: а — подвешенного; б — перекатывающегося; в — жидкого грузов
Сопоставляя рисунки (2, а) и (2, б), легко убедиться, что перекатывающийся груз оказывает точно такое же влияние на начальную остойчивость, как и груз, подвешенный в точке A. Положение этой точки определим радиусом кривизны l кривой, по которой перекатывается груз в данной плоскости наклонения. По аналогии с поправкой к метацентрической высоте, обусловленной перемещением подвешенного груза.снижение поперечной метацентрической высоты от влияния перекатывающегося груза будет равно
Его можно также трактовать, как результат переноса ЦТ груза в точку A — центр кривизны кривой BB 1. Следовательно, изменение аппликаты ЦТ судна равно
Жидкий груз Пусть на судне в цистерне, танке или отсеке имеется какой-либо жидкий груз. Если этот груз заполняет емкость, например, отсек, целиком, то при наклонении судна он переливаться не будет, его ЦТ останется на месте и в расчете остойчивости такой груз может рассматриваться как твердый. Если же груз заполняет отсек лишь частично и жидкость в отсеке имеет свободную поверхность, то при наклонении судна она будет переливаться, ЦТ груза сместится и это вызовет перемещение ЦТ судна. Ясно, что остойчивость судна при этом изменится. Рассмотрим вначале наклонение судна на угол Величина дополнительного кренящего момента при переливании груза будет определяться по формуле
Если бы груз p находился на судне, не имея возможности переливаться, как бы затвердев, то восстанавливающий момент согласно метацентрической формуле остойчивости был бы равен
где
представляет собой поправку к поперечной метацентрической высоте, учитывающую влияние свободной поверхности жидкого груза в отсеке на начальную остойчивость. Все величины, входящие в левую часть (33), положительны, поэтому поправка В случае, когда жидкие грузы со свободными поверхностями имеются в нескольких отсеках или цистернах, дополнительные кренящие моменты от их переливания суммируются и суммарная поправка к метацентрической высоте равна
где m — число отсеков и цистерн, имеющих свободные поверхности жидкостей, которые могут быть различными. Формула для поперечной метацентрической высоты, исправленной на влияние жидких грузов, имеет вид
По аналогии с этим выражением исправленную продольную метацентрическую высоту можно определить как
где
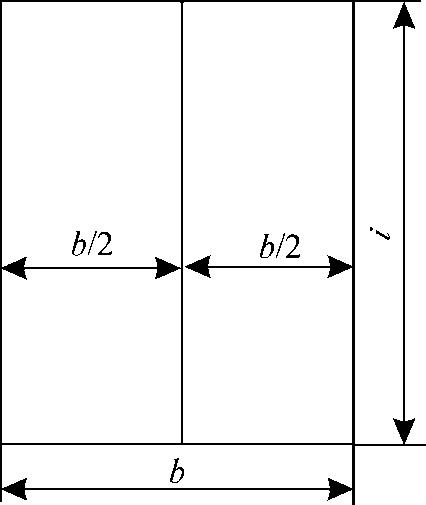
Здесь iyn — момент инерции свободной поверхности жидкости в отсеке относительно ее центральной поперечной оси, параллельной оси Oy. Для большинства надводных судов в неповрежденном состоянии поправка Для снижения влияния свободных поверхностей жидких грузов на поперечную остойчивость отсек или цистерну разделяют продольными непроницаемыми переборками. Предположим для простоты, что отсек имеет в плане форму прямоугольника длиной l и шириной b (рис. 3). Момент инерции свободной поверхности жидкости относительно ее центральной продольной оси в таком отсеке равен
Рис. 3. Отсек с продольной непроницаемой переборкой
Установим посередине отсека продольную непроницаемую переборку. Момент инерции свободной поверхности жидкости в отсеке будет равен сумме моментов инерции двух площадей свободной поверхности шириной b / 2 каждая:
Соответственно поправка к метацентрической высоте
уменьшится в 4 раза. Аналогичным образом легко показать, что при установке двух продольных переборок эта поправка уменьшится в 9 раз, а при установке n переборок в (n + 1)2 раз. Таким образом, разделение отсеков с жидкими грузами, имеющими свободную поверхность, непроницаемыми переборками является эффективным средством снижения влияния этих грузов на поперечную остойчивость судна. При приеме на судно жидкого груза p, координаты ЦТ которого xp, yp, zp, изменение начальной остойчивости должно определяться с учетом влияния свободной поверхности. Добавляя член, учитывающий это влияние в соответствии с (33), получим
где (D + p) — сила тяжести судна после приема груза. Подставляя
СТАТИКА КОРАБЛЯ (модули) д.т.н., профессор Борисов Р.В.
Санкт- Петербург 2012 г. МОДУЛЬ 1.МОРЕХОДНЫЕ КАЧЕСТВА И ТЕОРЕТИЧЕСКИЙ ЧЕРТЕЖ СУДНА
|
|||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 275; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.10.246 (0.143 с.) |
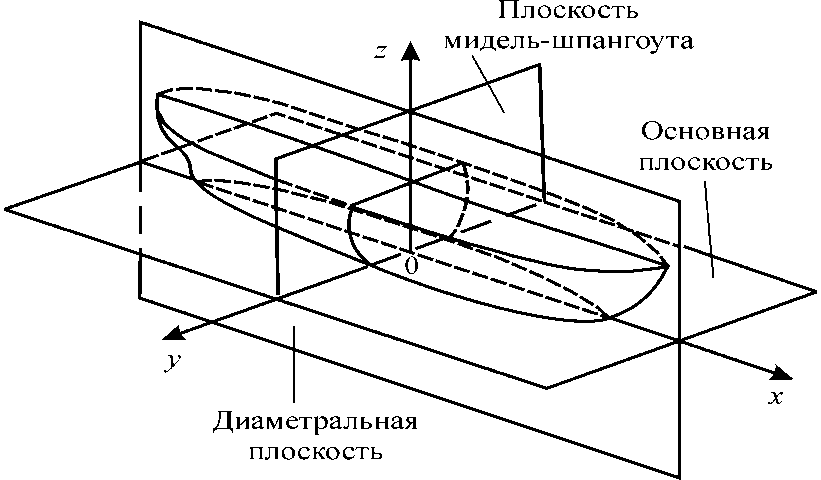


 направлена вверх перпендикулярно к действующей наклонной ватерлинии, а ось
направлена вверх перпендикулярно к действующей наклонной ватерлинии, а ось 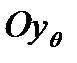 ей параллельна и направлена на правый борт. Эта система координат повернута относительно системы Oxyz около оси Ox на угол крена
ей параллельна и направлена на правый борт. Эта система координат повернута относительно системы Oxyz около оси Ox на угол крена 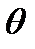 .
.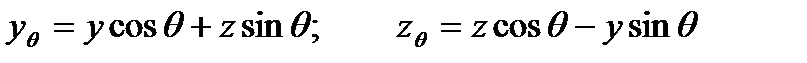 . (1)
. (1)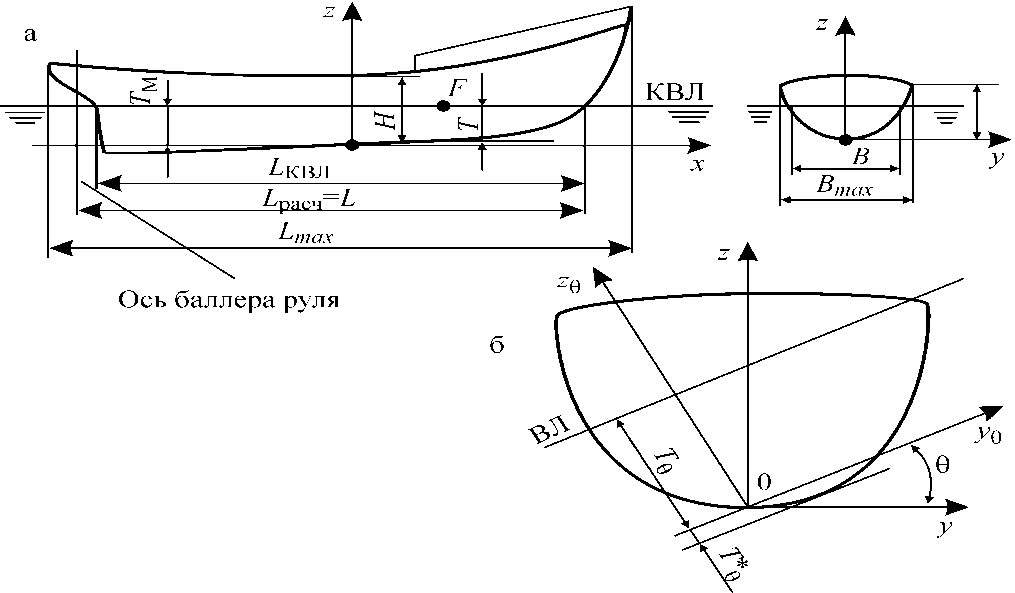
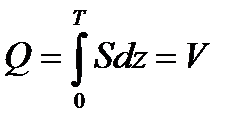 (21)
(21) . В соответствии с рис.4
. В соответствии с рис.4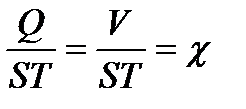 (22)
(22)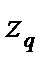 представляет собой в масштабе осадок аппликату центра величины судна. Из рис.4 видно, что
представляет собой в масштабе осадок аппликату центра величины судна. Из рис.4 видно, что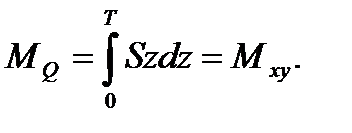
 .(23)
.(23)
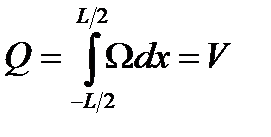 . (24)
. (24)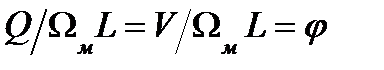 , (25)
, (25)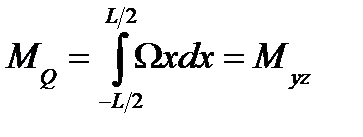 .
.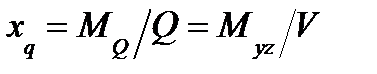 . (26)
. (26)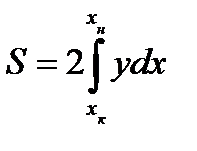 . (1)
. (1)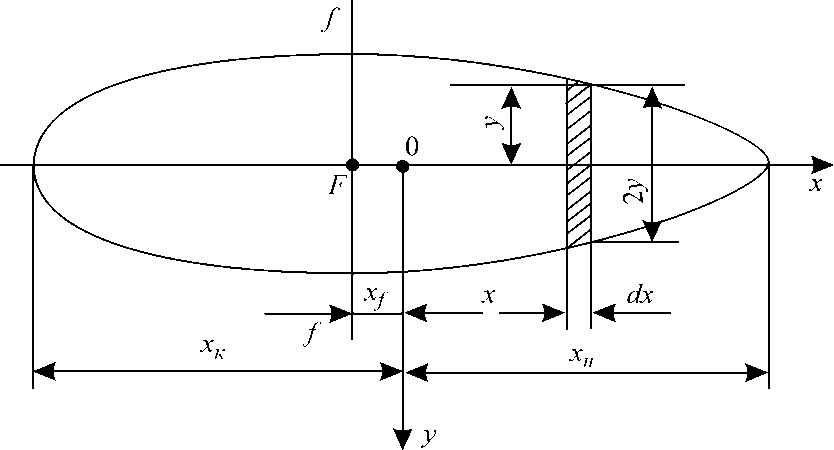
 . (3)
. (3)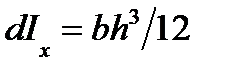 , где b = dx, h = 2 y, т. e.
, где b = dx, h = 2 y, т. e. .
.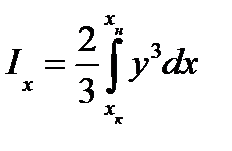 . (4)
. (4)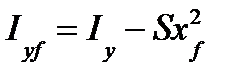 , (5)
, (5)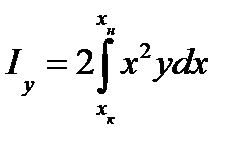 , (6) так как элементарный момент инерции площади dS равен
, (6) так как элементарный момент инерции площади dS равен 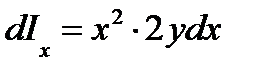 ; Sx 2 f — переносный момент инерции.
; Sx 2 f — переносный момент инерции.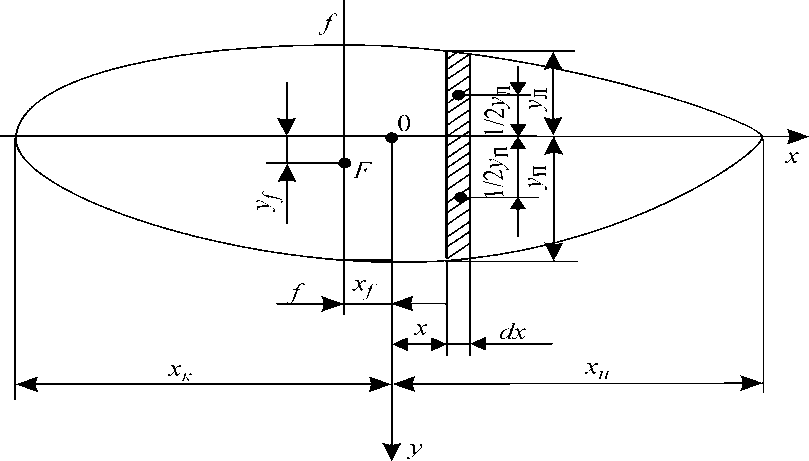
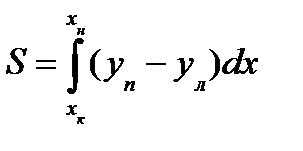 . (7) Аналогично для статического момента площади S относительно оси Оу получим
. (7) Аналогично для статического момента площади S относительно оси Оу получим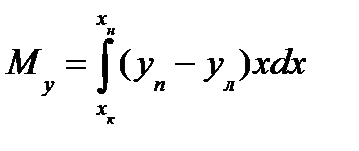 (8)
(8)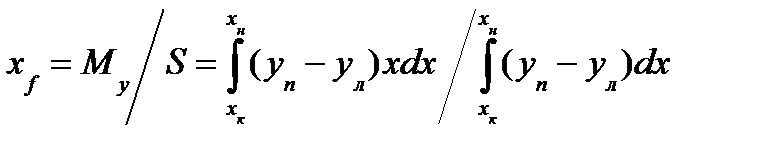 (9)
(9)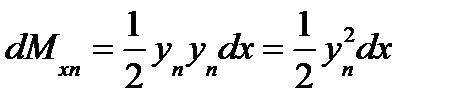 ,
,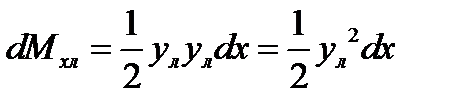 ,
,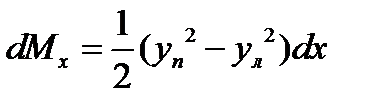
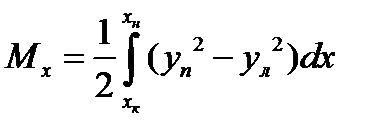 .(10)
.(10) . (11)
. (11) ;
;  .
. ; (12)
; (12)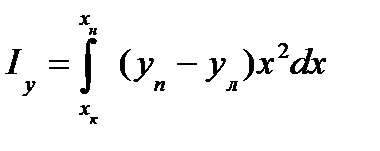 . (13)
. (13)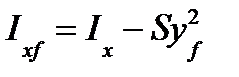 ;
;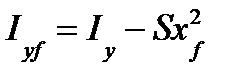 . (14)
. (14)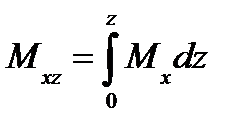 ,
,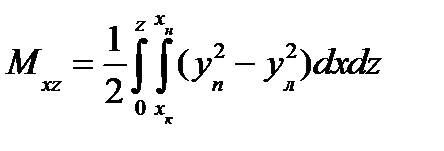 .
.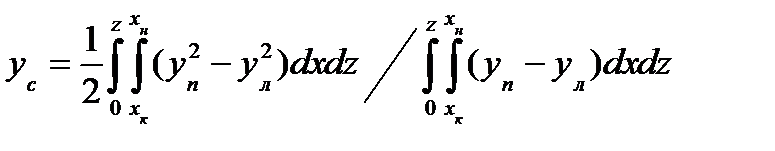 . (15)
. (15)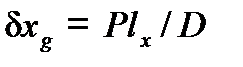 ;
; 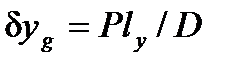 ;
;  . (1)
. (1)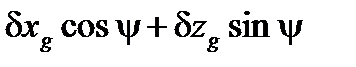 . Другая же будет действовать в поперечной плоскости, параллельной плоскости мидель-шпангоута, вызывая крен. Плечо ее будет равно
. Другая же будет действовать в поперечной плоскости, параллельной плоскости мидель-шпангоута, вызывая крен. Плечо ее будет равно 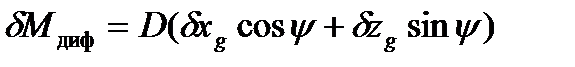 ;
;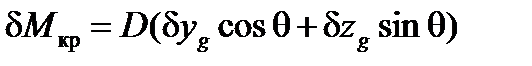 .
.
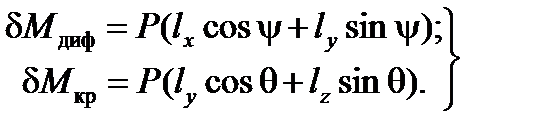 (2)
(2) 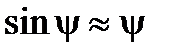 ;
; 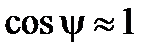 ;
; 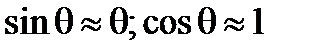 . Тогда формулы (2) принимают вид:
. Тогда формулы (2) принимают вид: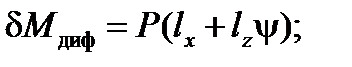
 (3)
(3)  ;
;  . (4)
. (4)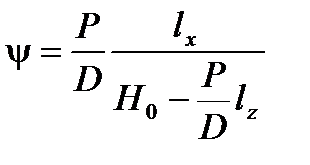 , (5)
, (5)  . (6)
. (6)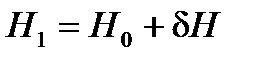 ; (7)
; (7)  , (8)
, (8)  .
.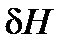 почти всегда можно пренебречь по сравнению с
почти всегда можно пренебречь по сравнению с 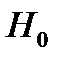 и положить
и положить 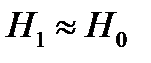 . Тогда, подставив (7) и (8) в формулы (5) и (6), окончательно найдем
. Тогда, подставив (7) и (8) в формулы (5) и (6), окончательно найдем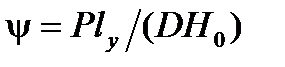 ;
; 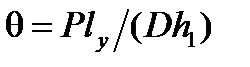 .(9)
.(9)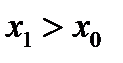 ,
,  , а значит и
, а значит и 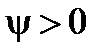 , т. е. судно получает дифферент на нос. Если же груз переносится в корму, то
, т. е. судно получает дифферент на нос. Если же груз переносится в корму, то 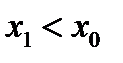 ,
, 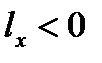 ,
,  , т. е. судно дифферентуется на корму. В случае переноса груза на правый борт
, т. е. судно дифферентуется на корму. В случае переноса груза на правый борт  и
и 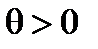 , а в случае переноса на левый
, а в случае переноса на левый 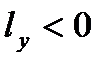 и
и 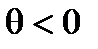 .
. . Благодаря такому перемещению груза образуется пара сил и дополнительный кренящий момент
. Благодаря такому перемещению груза образуется пара сил и дополнительный кренящий момент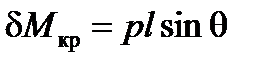 , (23)
, (23)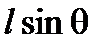 — расстояние, на которое переместился груз в поперечной плоскости. При достаточно малых наклонениях судна
— расстояние, на которое переместился груз в поперечной плоскости. При достаточно малых наклонениях судна . (24)
. (24)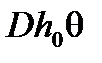 . Поэтому восстанавливающий момент с учетом влияния подвешенного груза равен
. Поэтому восстанавливающий момент с учетом влияния подвешенного груза равен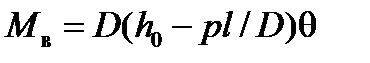 . (25)
. (25)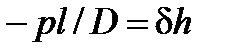 . (26)
. (26)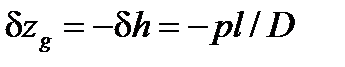 . (27)
. (27) . (28)
. (28)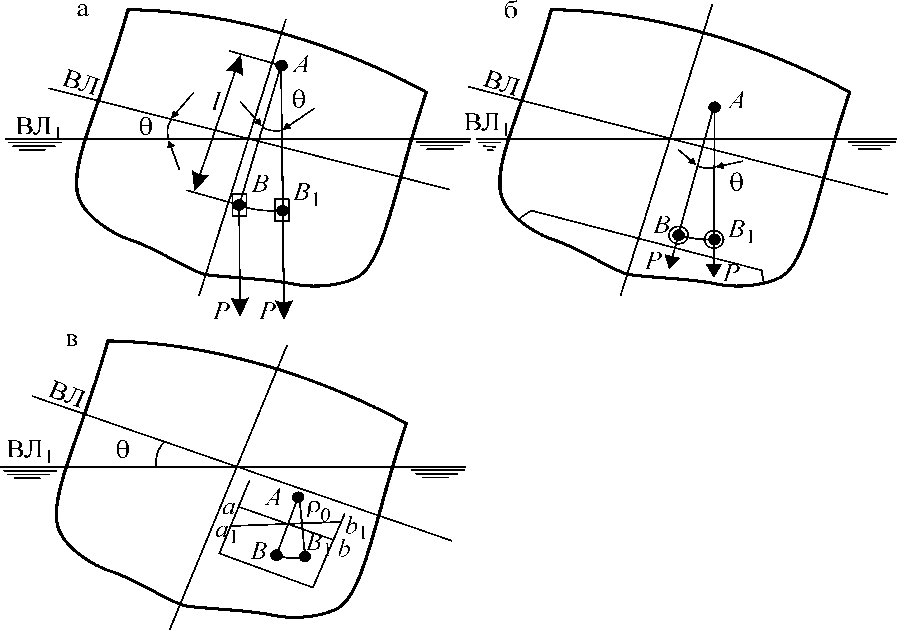
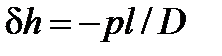 . (29)
. (29) . (30)
. (30)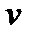 — объем жидкости в отсеке,
— объем жидкости в отсеке, 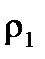 — ее плотность,
— ее плотность,  — объемное водоизмещение судна,
— объемное водоизмещение судна, 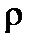 — плотность забортной воды;
— плотность забортной воды;  ;
; 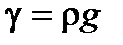 .
.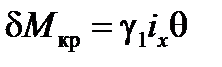 . (31)
. (31)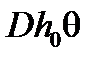 . При переливании груза он уменьшится на величину дополнительного кренящего момента
. При переливании груза он уменьшится на величину дополнительного кренящего момента  и будет равен
и будет равен , (32)
, (32)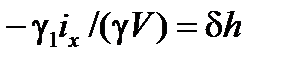 (33)
(33)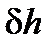 всегда отрицательна. Таким образом, жидкий груз со свободной поверхностью всегда уменьшаетначальную остойчивость судна. Важно отметить, что поправка
всегда отрицательна. Таким образом, жидкий груз со свободной поверхностью всегда уменьшаетначальную остойчивость судна. Важно отметить, что поправка 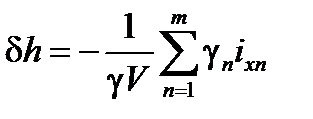 , (34)
, (34)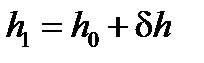 . (35)
. (35) , (36)
, (36)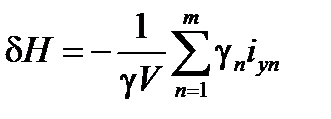 . (37)
. (37)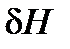 много меньше продольной метацентрической высоты H и в практических расчетах ее обычно не учитывают.
много меньше продольной метацентрической высоты H и в практических расчетах ее обычно не учитывают.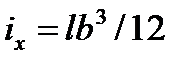 . Тогда поправка к метацентрической высоте на влияние свободной поверхности жидкого груза согласно формуле (33) будет равна
. Тогда поправка к метацентрической высоте на влияние свободной поверхности жидкого груза согласно формуле (33) будет равна .
.
 .
.
 ,
,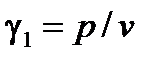 в правую часть этой формулы и вынося за скобку общий множитель
в правую часть этой формулы и вынося за скобку общий множитель 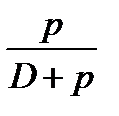 , находим
, находим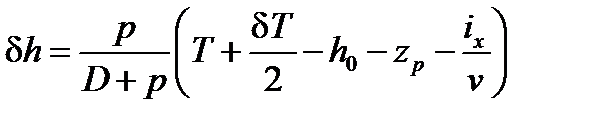 . (38)
. (38)


