Сложные проценты, или Восьмое чудо света

 

Кредит – необходимое условие для существования рынка. Перед тем как предложить что‑либо к продаже в качестве товара, это надо создать, или купить, или придумать, или быть готовым изготовить. Для этого нужно сначала потратить некое количество денег на изготовление, покупку или обучение, то есть использовать кредит. После продажи кредит обычно возвращается, а дополнительное количество денег, полученное в результате продажи, и составляет интерес продавца. Ссудив деньги заемщику, кредитор лишает себя возможности самому произвести нужный товар, продать его и увеличить таким образом имеющееся у него количество денег. За отказ от этой возможности он требует оплаты – кредит возвращается обычно в большем размере, чем исходно взятая сумма. Превышение возвращенной суммы над суммой взятого кредита называется процентами и составляет интерес кредитора. Обычно кредит выдается на определенное время, и величина процентов заранее оговаривается.

Например, в кредит выдается 1000 рублей на срок 6 месяцев под 18 % годовых. Это означает, что через полгода заемщик должен вернуть кредитору 1090 рублей (если бы срок кредита составлял 1 год, то через год надо было бы вернуть 1180 рублей). Такие расчеты называются расчетами по формуле простых процентов, и большинство краткосрочных кредитов выдается и возвращается по этим правилам. Формула для простых процентов выглядит следующим образом:

 

 

S = S₀(1+(i × t)/T),

 

где

S – возвращаемая сумма;

S₀ – сумма, взятая в долг;

i – процентная ставка за период времени T, которая здесь выражена не в процентах, а в долях единицы, то есть 18 % в нашей формуле запишутся как 0,18;

t – время пользования кредитом, выраженное в периодах T.

 

Однако не все кредиты можно описать с помощью данной формулы. Представим, что заемщик вовремя не смог рассчитаться с кредитором, не возвратив по истечении времени Т взятую в долг сумму. Представим также, что кредитора такой вариант развития событий не очень волнует и он не беспокоится о сохранности своих денег, абсолютно доверяя заемщику.

В этой ситуации кредитор и заемщик могут договориться о пролонгации кредита на тех же условиях (под те же проценты и на такой же срок), что и раньше, за исключением следующего факта. Поскольку на момент возврата кредита заемщик был должен уже не S₀, а S, то новой суммой, взятой в долг, будет уже S. Новая возвращаемая сумма S_new будет вычисляться как

 

 

S_new = S (1+(i × t)/T) = S₀ (1+(i × T)/T) (1+(i × t)/T).

 

Если и по окончании второго срока займа он не возвращается, то к концу третьего периода итоговая возвращаемая сумма уже будет вычисляться как

 

 

Snew_new = S₀ (1+(i × T)/T)² (1+(i × t)/T).

 

Если же заем возвращен спустя только m‑1 таких «пролонгаций» (или m периодов Т), то итоговая сумма «к получению» кредитором вычисляется по формуле:

 

 

S = S₀ (1+(i × T)/T)^m.

 

Эту формулу и называют формулой сложных процентов. «Сложность» их состоит в том, что за текущий период времени проценты начисляются как на саму исходную сумму займа, так и на начисленные на нее ранее проценты.

 

Папашу Ротшильда, основателя всемирно известной финансовой империи, как‑то попросили назвать семь чудес света. Он ответил: «Я затрудняюсь, но уверен, что восьмым чудом света являются сложные проценты».

 

Формула эта прокомментирована в сотнях учебников, рост суммы долга проиллюстрирован тысячами примеров. По мнению многих авторов, наиболее показательным, является следующий: если бы те 17 (или 27?) долларов, за которые в свое время остров Манхэттен был куплен у индейцев белыми колонистами, положить в тот момент под 3 % годовых с ежегодным причислением суммы процентов к сумме долга, то сумма выплаты на сегодняшний момент превышала бы стоимость Нью‑Йорка и Лос‑Анджелеса вместе взятых, со всеми их домами, мостами, автомобилями, кораблями и товарами.

 

Иначе говоря, белые колонисты сильно переплатили за тот кусок земли, на котором сейчас расположена центральная часть Нью‑Йорка. Вот бы моему преподавателю по истории КПСС в институте сейчас подкинуть этот расчетец! А то ведь в свое время пример с Манхэттеном нам преподносился не иначе как факт, иллюстрирующий угнетение белыми колонистами коренных жителей Северной Америки. А получается, что те белые парни сильно переплатили тем красным парням за простой кусок земли. Вот вам и угнетение!

 

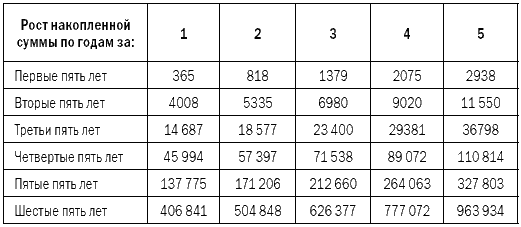
Нам кажется, что не менее интересный результат по формуле сложных процентов может быть получен и в течение жизни одного человека.

Предположим, человек начал откладывать по одному доллару в день (в долларах все‑таки еще привычней откладывать, чем в рублях). По окончании года все 365 отложенных долларов он дал кому‑нибудь в виде кредита сроком на один год под 24 % годовых (уверяю, под 2 % в месяц в России сегодня деньги разместить можно, а как это делается, мы будем обсуждать в дальнейшем). Но на этом наш уважаемый инвестор не остановился и продолжал откладывать по одному доллару в день. По истечении двух лет сумма, которую он таким образом накопил, составит 818 долларов (365 за второй год, 365 за первый и 88 долларов процентов, начисленных на сумму первого года). По истечении трех – 1379 долларов и так далее. Что произойдет, если человек будет продолжать действовать таким образом в течение 30 лет? Как будет прирастать отложенная сумма? Таблица 1 дает ответы на поставленные вопросы.

Результат, который мы получили, на наш взгляд, не менее показателен, чем пример с островом Манхэттен.

 

Таблица 1

Рост накопленной суммы по годам (при условии, что ежедневно «сберегается» один доллар и вся имеющаяся сумма ежегодно инвестируется под 24 % годовых)

 

В самом деле! Откладывая по одному доллару в день в течение 30 лет и размещая накопленное под 24 % в год, любой человек становится в течение своей жизни обладателем 964 тысяч долларов, то есть практически миллионером!

Это и есть основа основ любого богатства – система разумного сбережения и инвестирования средств. Другого пути нет. Кто‑то может возразить, что можно заработать и гораздо больше денег (и притом очень быстро), создав высокодоходный бизнес, либо получив главную роль в кассовом фильме, либо еще каким‑нибудь столь же легким способом. Наверное, это правильно. Но лишь с одной оговоркой – это могут сделать не все, а лишь единицы. Простой человек с улицы, не отличающийся никакими исключительными способностями, может стать богатым, лишь сберегая и инвестируя. Это, конечно, не так эффектно, как первая роль Шварценеггера или создание поисковика Google, но зато это может сделать ЛЮБОЙ человек!

 

2.2. Анализ процесса накопления, или «Ой, он и меня посчитал!»

 

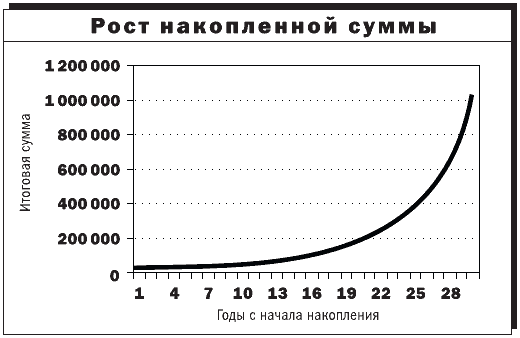
Проанализируем описанный в предыдущем разделе процесс роста миллионного состояния. Для наглядности данные из таблицы можно представить в виде графика (рис. 1).

Внимательно рассматривая эту картинку, можно сделать только один вывод: в начальный период накопления скорость роста состояния невелика. С течением времени она увеличивается и при приближении итоговой суммы к миллиону составляет уже величину, близкую к 200 тысячам долларов в год.

Давайте проанализируем процесс накопления более детально.

Рисунок 1. Рост накопленной суммы по годам (иллюстрация к табл. 1).

 

Человек, начавший накапливать состояние по вышеуказанной схеме (то есть откладывая в день по одному доллару и размещая в конце года всю накопленную сумму под 24 % годовых), за все время накопления отложит около 11 тысяч долларов:

 

 

30 лет × 365$ = 10 950$

 

К концу же периода накопления по описываемой нами схеме он будет обладать суммой в 963 964$, то есть во много раз большей. Финансовые аналитики сказали бы, что коэффициент мультипликации для выбранной тридцатилетней схемы равен:

 

 

963 934$ / 10 950 $ = 88,1

 

Иначе говоря, каждый доллар, вложенный в эту схему в течение срока ее действия, на выходе увеличится в 88,1 раза!

Давайте проделаем небольшой численный эксперимент. Предположим, что в первый год было вложено не 365$, a 364$. Например, в один из дней первого года накопления наш «сберегатель» забыл опустить монету в заветную коробочку. Во всем остальном ситуация с его деньгами была полностью аналогичной описанной выше. Если честно повторить все вычисления, то окажется, что через тридцать лет итоговая сумма «к получению» будет 963 422$, то есть на 512$ меньше!

Получаем интересный вывод: для каждого доллара, внесенного в нашу схему в течение первого года накопления, коэффициент мультипликации равен 512!

Вывод, в общем‑то, очевидный. Действительно, в соответствии с формулой сложных процентов каждый доллар, внесенный в течение первого года в накопительную схему, через 29 лет даст сумму, равную 1$ х (1+0,24)29, то есть 511,95$. Повторяя вычисления для «забытого быть отложенным» доллара во второй год, получим коэффициент мультипликации 413, в третий – 332, в четвертый – 268 и т. д. Рассуждая далее, придем к выводу, что наибольший вклад в получение миллиона путем накопления вносят деньги, внесенные в первые годы работы схемы. Действительно, деньги, отложенные в последний год, не принесут дополнительного дохода, поскольку их просто не успеют инвестировать (в нашем случае – положить под проценты).

Проведем еще один эксперимент. Предположим, что накопление ведется следующим образом: ежегодно откладывается по 365$, которые затем вкладываются под 24 % в год, но процедура эта повторяется только первые 10 лет из 30. В последующие 20 лет новые суммы не откладываются, просто продолжается процесс получения и перевложения начисленных процентов. Полученная таким образом сумма через 30 лет будет составлять 853 120$, а через 31 год – 1 057 869$. То есть ТОЖЕ МИЛЛИОН, но за 31 год!

Вывод, который напрашивается сам собой, кому‑то покажется очевидным, а кому‑то – удивительным.

Чтобы стать миллионером в течение жизни, необязательно отказывать себе в сумме в 1$ каждый день в течение 30 лет. Можно «потерпеть» первые 10–12 лет, а потом жить, тратя на всю катушку (аж на целый доллар в день больше!), поскольку будущее уже обеспечено! Главная же особенность процесса накопления такова: чем раньше начнешь, тем раньше сможешь воспользоваться результатами своей бережливости.

 

От этих, прямо скажем, полудетских вычислений и рассуждений еще очень далеко до настоящего богатства, но это, так сказать, пока только теоретическая база. Специалисты, конечно, добавят, что и база‑то какая‑то несолидная. В ответ на это можем возразить, что и само богатство тоже вещь не очень сложная. Это просто много денег.

 

Приведенная в предыдущем разделе таблица дает много пищи для размышлений. Давайте с ее помощью ответим на вопрос, что будет, если откладывать в день не один доллар, а два? Очевидно, что миллион мы накопим тогда, когда в клетке таблицы будет стоять цифра, близкая к 500 тысячам (умноженные на 2, эти 500 тысяч и дадут вожделенный миллион). Это произойдет на 27‑м году процесса накопления, то есть на три года раньше.

А если откладывать по два доллара в день, но при условии, что начальный капитал в сумме, например, 10 000$, уже имеется? Оказывается, в этом случае заветной цифры в один миллион можно достичь за каких‑нибудь 17 лет! То есть молодой человек 20–22 лет, имея начальный капитал и пользуясь предложенной схемой накопления, может легко стать финансово независимым к своему сорокалетию!

Заканчивая процесс анализа формулы сложных процентов, сделаем одно замечание. В полном курсе финансовых вычислений (который изучают специалисты по финансовому рынку) есть такие понятия – сегодняшняя стоимость будущей суммы и будущая стоимость сегодняшней суммы. В нашем случае для 1$, отложенного в первый год накопления, его будущая стоимость равна 512$. А 512$, которые можно получить через 30 лет, стоят сегодня всего лишь 1$.

Многие экономисты называют процесс роста суммы накоплений «ростом финансового дерева». Этот процесс и в самом деле немного похож на рост дерева. Сначала из земли появляется один росток. Затем на нем образуется новый побег. Потом – еще один побег и маленький отросток на первом побеге. Затем на каждом из отростков появляются новые, которые, в свою очередь, тоже ветвятся. Теоретически процесс ветвления может быть бесконечным. В итоге масса ветвей может превысить массу ствола в десятки и сотни раз.

Точно так же происходит и накопление денежной суммы. На первый отложенный доллар нарастают проценты, которые, в свою очередь, дают побеги в виде процентов и так далее, и так далее. Богатство, полученное в конце процесса накопления, может в десятки и сотни раз превышать изначально вложенные суммы.

Предположим, мы решили не пускать на самотек процесс обеспечения собственной старости и начали, наперекор скептикам, копить миллион. Чтобы проводить вычисления в течение ближайших 30 лет не задумываясь (и не считать, что доллар, отложенный в первый год, даст 512$, а в седьмой – только 113$), используем следующий метод приближенных вычислений.

Поскольку 1$ первого года превращается в 512$, а 1$ тридцатого года накопления не увеличивается, примем, что в среднем наша схема накопления увеличивает вложенную в нее сумму в 250 раз (почти половина от 512). Так будет легче производить вычисления. Будем считать, что независимо от того, на каком году действия нашей схемы мы вкладываем (либо не вкладываем) в нее деньги, реально мы получаем (либо тратим) в 250 раз больше.

Заметим, что умножать на 250 очень просто даже в уме. Нужно сначала умножить число на 1000, а затем разделить на 4. Например, аппетитный пирожок с капустой стоит 12 рублей. Умножаем на 1000 – получаем 12 000 рублей. Теперь делим на 4 – получаем 3000 рублей. Таким образом, будущая стоимость сегодняшнего пирожка с капустой составляет 3000 рублей, или более 100$.

Может быть, воздержаться от его покупки?

 

Как‑то на двухдневном семинаре по управлению личными финансами в конце первого дня я задал всем слушателям домашнее задание – купить абсолютно бесполезную вещь стоимостью до 100 рублей, получить в магазине чек на эту покупку и принести ее на занятия.

Лучше всех задание выполнил здоровенный детина бандюганского вида. Он купил фигурку зайчика из искусственного (!) нефрита стоимостью, по‑моему, 78 рублей. Все условия задания он выполнил. Вещь абсолютно бесполезная, недорогая, чек наличествует. На семинаре мы поговорили о реальной стоимости этой вещи (78 х 250 = 19 500 рублей), о том, что наши квартиры набиты такими вещами, и т. д.

Спустя несколько месяцев этот парень приглашает меня в гости. Приезжаю. В красном углу, на телевизоре, стоит уже хорошо знакомый мне зайчик, к шее которого шелковыми шнурками прикреплены две заламинированные бумажки.

Первая – чек из магазина на покупку этого зайчика. Вторая – собственноручно изготовленный хозяином дома ярлык. На нем написано: «Этого зайчика я купил 25.04.02 за 650$. Это последняя абсолютно бесполезная вещь, которую я купил в своей жизни». И дальше не я, а уже хозяин дома прочел мне лекцию о том, что этот зайчик – самая дорогая для него вещь в его квартире. Дорогая не в смысле стоимости, а в смысле самая важная. Потому что каждый раз, когда хочется что‑нибудь купить, он вспоминает этого зайчика и очень часто воздерживается от покупки. Если верить ему, то благодаря зайчику менее чем за полгода он сэкономил более 3000$. «А ведь это на самом‑то деле 750 000$!» – сказал он мне.