Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общая характеристика и виды моделей в теории надежностиСодержание книги
Поиск на нашем сайте
При определении показателей надежности объект может быть рассмотрен как элемент или как система. Элемент – любое устройство, сооружение, машина, аппарат, надежность которых изучают независимо от надежности составляющих его частей, то есть элемент считают неделимым. Под системой понимается совокупность элементов (или подсистем), объединенных конструктивно или функционально в соответствии с заданным алгоритмом взаимодействия при выполнении определенной задачи в процессе применения по назначению. Для системы известны показатели надежности составных частей (элементов) и установлено влияние отказа каждого элемента на отказ системы. В соответствии с представленной классификацией в теории надежности существуют два направления, родственные по идеологии и общим понятиям, но отличающиеся по подходу к решению задач. Первое направление – системная, статистическая, или математическая, теория надежности, второе направление можно условно назвать физической теорией надежности. В рамках этих направлений существуют два больших класса математических моделей надежности: структурные и функциональные. В структурных моделях осуществляется определение значений показателей надежности объекта, обусловленное надежностью его элементов и разветвленностью связей между элементами. Они основаны на логических схемах взаимодействия элементов, входящих в систему, с точки зрения сохранения работоспособности системы в целом. При этом используют статистическую информацию о надежности элементов без привлечением сведений о физических свойствах материалов, о внешних нагрузках и воздействиях, о механизмах взаимодействия между элементами. Структурные модели представляются в виде схем и графов, а исходную информацию задают в виде известных значений вероятностей безотказной работы элементов, интенсивностей их отказов и т.д. Расчет функциональной надежности – это определение показателей надежности выполнения объектом заданных функций. Поэтому такие показатели зависят от ряда действующих факторов (вида заданной функции, структурной надежности, математического и программного обеспечения, работы операторов), то как правило расчет функциональной надежности более сложен, чем структурный. Функциональные модели учитывают механические, физические и другие реальные процессы, которые ведут к изменению свойств объекта. Такие модели широко применяются в расчетах машин и конструкций. Именно в этой области впервые были поставлены вопросы надежности (в связи со статистическим истолкованием коэффициента запаса прочности и допускаемых напряжений). Показатели надежности отдельных элементов (деталей) оценивают на основе физических моделей, в то время как для оценки показателей надежности изделий в целом чаще используются модели системной теории надежности. Резервирование систем Системы с позиции надежности могут быть последовательными, параллельными и комбинированными. В последовательных системах потеря работоспособности любого технического объекта приводит к отказу всей системы. В системах с параллельным соединением технических объектов отказ одного из них не приводит к отказу всей системы. Например, трехэкскалаторный подъем на станциях метро. К параллельным системам относятся так называемые системы с резервированием. В это понятие включается структурное резервирование, которое достигается введением в систему резервных элементов, избыточных по отношению к структуре с минимально необходимым по функциональному назначению числом элементов (или агрегатов). При этом различают постоянное резервирование с нагруженным резервом, когда резервный элемент работает наряду с основным и принимает на себя функции основного при отказе последнего. Существуют системы с ненагруженным резервом, когда резервный элемент (агрегат) не участвует в нормальном рабочем процессе, включаясь лишь при отказе основного элемента (агрегата). Наконец, различают резервирование с резервом, работающим в облегченном режиме. Простейшая зарезервированная система постоянного резервирования показана на рис. 2.
Если вероятность отказа i -го элемента Pi (t), то вероятность отказа всех элементов (основных и резервных) определяется по теореме умножения вероятностей (как вероятность проявления совместно независимых событий) P отк (t) = P 1отк (t) × P 2отк (t) … × Pn отк (t) = Вероятность безотказной работы будет: P (t) = 1 – P отк (t). При одинаковых элементах F 1(t) = Fi (t), i = 2,…, n P (t) = 1 – Fin (t). В системах с последовательным соединением (блоков) вероятность безотказной работы определяется по теореме умножения вероятностей как произведение вероятности элементов (блоков): P = Pа (t) × Pb (t). При резервировании замещением резервные элементы (блоки) включаются только при отказе основных. Подключение резервных элементов (блоков) может осуществляться либо оператором по сигналам приборов, свидетельствующим о режиме функционирования системы, либо автоматически. В теории надежности доказывается, что поэлементное резервирование более эффективно, чем общее, а резервирование замещением при совершенно надежном подключении эффективнее, чем постоянное.
Вопросы для самопроверки 1. Определите понятие «надежность»? 2. Определите понятие «показатель надежности». 3. В каких пределах может изменяться вероятность безотказной работы? 4. Что такое гамма-процентная наработка до отказа? 5. Как можно определить плотность распределения отказов? 6. Как рассчитать интенсивность отказов? 7. Как определить вероятность восстановления объекта. 8. Назовите основной показатель долговечности изделия. 9. Назовите одну из основных причин появления отказов. 10. Как оценить вероятность безотказной работы системы с резервированием?
ОСНОВЫ ТЕОРИИ ГРАФОВ
Теория графов – это раздел дискретной математики, исследующий свойства конечных множеств с заданными отношениями между их элементами. Графы представляют собой наиболее абстрактную структуру, с которой приходится сталкиваться в курсах математической логики, дискретной математики, теории сетей связи. Любая система, предполагающая наличие дискретных состояний или узлов и переходов между ними, может быть описана графом. Граф – это совокупность вершин (узлов) и связывающих их ребер (ветвей). Графы отображаются на плоскости набором точек и соединяющих их линий или векторов. При этом ветви могут отображаться и кривыми линиями, а их длина не играет никакой роли. Граф называется ориентированным (или орграфом),если некоторые ребра имеют определенное направление, Это означает, что в орграфе некоторая вершина может быть соединена с другой вершиной, а обратного соединения нет. Ребра орграфа называются дугами. Смежные вершины графа - вершины, инцидентные одному я тому же ребру (принадлежащие одному ребру). Ребро графа определяется парой вершин. Два ребра, инцидентные одной и той же вершине (у которых есть общая вершина), также называются смежными (или соседними). Математически граф G можно описать упорядоченной парой множеств N и А: G = (N, А), где N – непустое множество, называемое множеством вершин; А – множество ребер, отражающее отношение между вершинами. Граф, в котором направление линий не выделяется (все линии являются ребрами), называется неориентированным;граф,в котором направление линий принципиально(линии являются дугами) называется ориентированным. Часть графа – граф, образованный из исходного удалением некоторых вершин и ребер. Подграфом называется часть графа,образованная подмножествомвершин вместе со своими ребрами (дугами), соединяющими вершины из этого множества. Суграф – часть графа, образованная удалением из исходного графа некоторых ребер. Петлей называется ребро, концевые точки которого совпадают. Степенью (валентностью) вершины называется число инцидентных ей ребер. Кратностью пары вершин называется число соединяющих их ребер. Ветви дерева – ребра графа, вошедшие в дерево. Хорды – ребра графа, не вошедшие в дерево. Две вершины называются смежными, если они соединены ребром (дугой). Смежные вершины называются граничными вершинами соответствующего ребра (дуги), а это ребро (дуга) – инцидентным соответствующим вершинам. Графы равны, если множества вершин и инцидентных им ребер совпадают. Графы, отличающиеся только нумерацией вершин и ребер, называются изоморфными. Ребра, инцидентные одной паре вершин, называются параллельными или кратными. Вершины графа, которые не принадлежат ни одному ребру, называются изолированными. Граф с кратными ребрами называется мультиграфом. Граф, содержащий петли (т.е. некоторая вершина соединена сама с собой ребром) и кратные ребра, называется псевдографом. Конечный граф–число вершин и ребер конечно. Полный граф–граф без петель и кратных ребер,каждая пара вершинсоединена ребром. Граф является связным, если можно указать маршрут, охватывающий все вершины. Дерево графа - связный граф, не имеющий циклов. Фундаментальное дерево (остов) - связный граф, не имеющий циклов. Примеры графа, подграфа, суграфа и фундаментального дерева представлены на рис. 1.
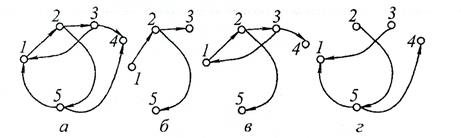
Рис. 5.1 Структуры: а – граф; б – подграф; в – суграф; г – фундаментальное дерево
Маршрут в графе–это последовательность ребер,в которых каждыедва соседних ребра имеют общую вершину. Причем одно и то же ребро может встречаться в маршруте несколько раз. Маршрут называется циклом, если в нем первая вершина совпадает с последней. Цепью называется множество ребер,которые можно расположить так,что конец одного ребра является началом другого. То есть цепь – это маршрут в неографе, в котором все ребра разные. Замкнутая цепь также называется циклом. Путем называется последовательность дуг(в ориентированном графе),такая, что конец одной дуги является началом другой дуги. Простой путь – путь, в котором ни одна дуга не встречается дважды. Элементарный путь – путь, в котором ни одна вершина не встречается дважды в графе. Контур –это цикл без повторения вершин,за исключением первойвершины, совпадающей с последней. Длиной пути (контура) называется число дуг пути (или сумма длин его дуг, если последние заданы). Последовательности вершин (рис. 5.1): 1–2–3–4–2–5 не простой путь, маршрут; последовательности 1–2–3–4–7–5 и 1–2–5 – простые пути; 1–2–3–4–2–5–6–1 – это цикл (но не контур); 1–2–5–6–1 – это контур. Если имеется некоторый маршрут из вершины t в вершину s, заданный графа, называется гамильтоновой цепью (соответственно – циклом, путем, контуром). Простая цепь (цикл, путь, контур), содержащая все ребра (дуги) графа, называется эйлеровой цепью (соответственно – циклом, путем, контуром). Граф называется связным, если любые две его вершины можно соединить маршрутом (цепью или путем). Ребро, при удалении которого граф перестает быть связным, иногда называют мостом или перешейком. Если граф не является связным, то его можно разбить на связные подграфы, называемые компонентами. Связностью графа называется минимальное число ребер, после удаления которых, граф становится несвязным. Для ориентированных графов: если любые две вершины графа можно соединить путем, то граф называется сильно связным. Связный граф, в котором существует эйлеров цикл, называется эйлеровым графом. Степень вершины –это число ребер,входящих в эту вершину.Вершинаназывается висячей, если ее степень равна единице. Матрицы графов Важным вопросом, особенно для приложений теории графов, является определение возможных способов представления графов. Самый простой способ – полное перечисление множеств X и V. Однако в этом случае выявление у графа различных характеристик и свойств будет крайне затруднительным. Граф можно представить в виде некоторого графического изображения и визуально определить некоторые свойства и характеристики заданного графа. Однако при наличии большого числа ребер и вершин этот способ также мало пригоден. Лучше всего представить граф в числовом виде, в виде матрицы. Матрица смежности. Это квадратная матрица А(G) порядка п (п – число вершин), в которой нули стоят по главной диагонали (если в графе нет петель, а если петли есть в вершине k (и число этих петель равно р), то на главной диагонали в строчке с номером k стоит число р). Если вершина i связана с вершиной j одним ребром, то элемент матрицы смежности aij равен единице, если эти вершины связаны s ребрами, то аij= s. Аналогичным образом строятся матрицы смежности для орграфов и для мультиграфов. Матрица инцидентности –это матрица B(G) размера n - m,где n – число вершин, а m – число ребер графа, при этом ее элементы kij равны 1, если вершина с номером i является для ребра с номером j начальной или конечной (если ребро неориентировано) и начальной для ориентированных ребер. Для ориентированного графа матрица достижимости – это квадратная матрица C(G) размера порядка п (п – число вершин), в которой нули стоят по главной диагонали (если в графе нет петель, а если петли есть в вершине k (и число этих петель равно р), то на главной диагонали в строчке с номером k стоит число р). Если вершина j достижима из вершины i одной дугой, то элемент матрицы достижимости сij равен 1, если эти вершины связаны s дугами, то аij= s.
|
||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 190; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.225.188 (0.01 с.) |

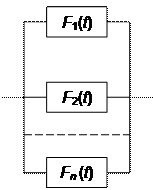 Рис. 4.4 Схема резервирования
Рис. 4.4 Схема резервирования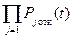 .
.