
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Физическое и математическое моделированиеСодержание книги
Поиск на нашем сайте
Кафедра Машиностроения Допущены к проведению занятий в 2016-2017 уч.году Заведующий кафедрой профессор В.В. Максаров «__» сентября 2016 г.
ТЕКСТЫ ЛЕКЦИЙ по учебной дисциплине «МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ В МАШИНОСТРОЕНИИ» Специальность (направление подготовки): 15.03.01«Машиностроение» Специализация (профиль): Технология, оборудование и автоматизация машиностроительных производств Разработали: доцент Алексеева Л.Б. Обсуждены и одобрены на заседании кафедры Протокол № 1 от 29 августа 2016 г. САНКТ-ПЕТЕРБУРГ 2016 ВВЕДЕНИЕ Моделирование в научных исследованиях стало применяться еще в глубокой древности и постепенно захватывало все новые области научных знаний: техническое конструирование, строительство и архитектуру, астрономию, физику, химию, биологию и, наконец, общественные науки. Большие успехи и признание практически во всех отраслях современной науки принес методу моделирования ХХ в. Под моделированием понимается процесс построения, изучения и применения моделей. Оно тесно связано с такими категориями, как абстракция, аналогия, гипотеза и др. Процесс моделирования обязательно включает и построение абстракций, и умозаключения по аналогии, и конструирование научных гипотез. Главная особенность моделирования в том, что это метод опосредованного познания с помощью объектов-заместителей. Модель выступает как своеобразный инструмент познания, который исследователь ставит между собой и объектом и с помощью которого изучает интересующий его объект. Именно эта особенность метода моделирования определяет специфические формы использования абстракций, аналогий, гипотез, других категорий и методов познания. Применительно к естественным и техническим наукам принято различать следующие виды моделирования: · концептуальное моделирование, при котором совокупность уже известных фактов или представлений относительно исследуемого объекта или системы истолковывается с помощью некоторых специальных знаков, символов, операций над ними или с помощью естественного или искусственного языков;
· физическое моделирование, при котором модель и моделируемый объект представляют собой реальные объекты или процессы единой или различной физической природы, причем между процессами в объекте-оригинале и в модели выполняются некоторые соотношения подобия, вытекающие из схожести физических явлений; · структурно-функциональное моделирование, при котором моделями являются схемы (блок-схемы), графики, чертежи, диаграммы, таблицы, рисунки, дополненные специальными правилами их объединения и преобразования; · математическое (логико-математическое) моделирование, при котором моделирование, включая построение модели, осуществляется средствами математики и логики; · имитационное (программное) моделирование, при котором логико-математическая модель исследуемого объекта представляет собой алгоритм функционирования объекта, реализованный в виде программного комплекса для компьютера. ВВЕДЕНИЕ В МОДЕЛИРОВАНИЕ Инженерные задачи Традиционно инженерные задачи классифицируют по видам инженерной деятельности:технологические, конструкторские, исследовательские и управленческие; по целевому назначению:задачи исследования, проектирования, прогнозирования и оптимизации. Технологические задачи связаны с проблемами разработки и реализации в условиях конкретного производства различных технологий. При этом технология рассматривается как некоторый алгоритм действий, последовательность этапов, операций, переделов и переходов, характеризующихся индивидуальным содержанием и выполняемых с использованием конкретных оборудования, оснастки и необходимых ресурсов. Результат решения таких задач обычно оформляется в виде комплекта технологической документации, технологических карт, инструкций, руководящих материалов, позволяющих получить ответы на вопросы о структуре технологической цепочки и параметрах технологического режима; реже – в виде управляющих программ для автоматических модулей технологического назначения. Конструкторские задачи связаны с проблемами поиска рациональных геометрических форм, структуры, материала и режимов эксплуатации изделий, оснастки, оборудования, реже – объемно-планировочных решений при выполнении работ по проектированию новых или реконструкции действующих производственных подразделений. Результат решения таких задач обычно оформляется в виде комплекта конструкторской документации, рабочих и сборочных чертежей, спецификаций, схем, планировок, эскизов, 2D- и 3D-визуализаций, компьютерных программ для изготовления деталей изделий, оснастки, оборудования на станках с ЧПУ,
Исследовательские задачи связаны главным образом с «узкими местами» производства, изучением причинно-следственных связей явлений, имеющих место в производственных процессах, проведением технологического контроля материалов, изделий оснастки и оборудования; выявлением производственного брака, его профилактикой и устранением; реже – разработкой новых исследовательских методик и их освоением. Результаты решения таких задач обычно оформляются в виде заключений, актов, предложений, рекомендаций и технических отчетов, позволяющих не допускать, снижать или ликвидировать имеющиеся либо обнаруженные технические недостатки действующего или проектируемого производства. Управленческие задачи (задачи менеджмента) связаны с проблемами организации производства и управления его подразделениями, согласованием режимов их работы, планированием ремонтов оборудования и оснастки, распределением ресурсов, рационализацией грузопотоков, сопровождением и обеспечением производственных процессов. Результаты их решения – планы, графики, заявки, маршрутные листы, приказы, распоряжения. Задачи исследования ориентированы на изучение природы явлений, происходящих внутри объекта, а также связывающих его с окружающей средой; выявление существенных характеристик и свойств объекта, форм и связей между ними, возможностей влияния на них извне и управления ими. Задачи проектирования нацелены на создание новых или совершенствование имеющихся объектов на основе их структурно-функциональных характеристик и оценки недостатков и противоречий аналогов и прототипов. Задачи прогнозирования имеют целью получить ответ на вопрос о том, что произойдет с объектом, его структурой и параметрами при изменении условий его существования (приложение дополнительных внешних воздействий, смена их характера, исключение из структуры объекта одной или нескольких составляющих, переход на альтернативные виды материалов и ресурсов и т. п.). Задачи оптимизации ориентированы на улучшение характеристик и свойств объекта, а также поиск наилучшего варианта решения из множества всех возможных в отношении данного объекта. Следствием системного подхода к изучению объектов является возможность применения к решению инженерных задач общего метода моделирования. Моделирование – это универсальный метод изучения объектов, основанный на упрощении представлений о них. Именно упрощение составляет ядро, сущность и главную идею моделирования, позволяя делать процесс изучения объектов, даже самых сложных, менее трудоемким и затратным. Так, в соответствии с общепризнанной концепцией «жизненного цикла» теория систем описывает существование любого объекта непрерывной замкнутой цепочкой-петлей: «проектирование – реализация – эксплуатация – моральное и физическое старение – переработка или утилизация – обновление». На каждом этапе (звене) этой цепочки удобно рассматривать объект с определенной стороны, в определенном аспекте, принимая во внимание не все, а лишь некоторые, наиболее существенные, его качества и свойства, т. е. упрощая его.
В инженерной практике чаще всего используют две формы упрощения объектов, основанные на принципах разукрупнения и идеализации. Разукрупнение, или детализация, заключается в реальном или абстрактном разделении объекта как системы на обладающие относительной автономией части – подсистемы с последующим изучением каждой из частей по отдельности и обобщением, «склеиванием», результатов. Идеализация –замена реального объекта другим, идеализированным, обладающим только теми чертами и свойствами, которые важны для решения данной инженерной задачи и удобны для количественной и качественной оценки. Примерами применения на практике принципа разукрупнения могут служить: поузловой метод проектирования машин; исследование технологического процесса с выделением отдельных операций; методика послойного конструирования в среде графических пакетов типа AutoCAD. В качестве примеров применения на практике принципа идеализации можно привести: введение целого ряда допущений при построении и использовании расчетных схем, проектных и проверочных методик; замену сложных геометрических форм стандартными техническими при конструировании изделий и оснастки; усреднение количественных значений свойств материалов по всему объему изделий. Особая роль моделирования в инженерной практике проявляется в создании благоприятных предпосылок к решению большинства инженерных задач; реализации системного подхода к изучению объектов; обеспечении возможностей для применения к изучению объектов других методов исследования, таких как аксиоматический, исторический, анализа-синтеза; в формировании четкого алгоритма решения не одной, а целого класса задач. Вопросы для самопроверки 1. Дайте характеристику основных положений теории моделирования. 2. В чем суть физического моделирования? 3. Какое моделирование называют масштабным? 4. Какое моделирование называют полунатуральным? 5. Перечислите виды физического подобия. 6. В чем отличие физического от математического моделирования? 7. Как называется сходство модели и оригинала по одному из признаков их формы и структуры?
8. В чем суть системного подхода, используемого при решении инженерных задач? 9. Что такое иерархичность? 10. Перечислите традиционно инженерные задачи. 11. Какие проблемы решаются в технологических задачах? 12. Что понимается под формализмом? 13. Как оценивается сложность объекта? 14. Укажите, какие задача решаются с помощью идеализации объекта. 15. Поясните суть детализации. 16. Как оценивается структурная сложность? 17. Поясните термин параметрическая сложность. 18. Что такое изоморфизм? 19. Дайте определение мономорфизма. 20. Что такое полиморфизм? 21. Что понимается под принципом упрощения? 22. Какие требования предъявляются к математическим моделям? 23. Как оценивается точность математических моделей? 24. Как оценивается степень универсальности математических моделей? 25. В чем суть имитационного моделирования? 26. В чем суть аналитического моделирования? 27. Что отображают аналоговые математические модели? 28. Что отражает принцип несоответствия? 29. Какие математические модели называют дискретными? 30. Что понимается под адекватностью математической модели? 31. В чем суть концептуальной постановки задачи моделирования. 32. Как оценивается адекватность модели? 33. От чего может зависеть решение о точности модели? 34. В чем суть концептуальной постановки задачи моделирования. 35. В каком виде реализуются математические модели? 36. Как оценивается адекватность модели? 37. Виды алгоритмических моделей 38. От чего может зависеть решение о точности модели? ТЕОРИЯ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА Планирование эксперимента В настоящее время благодаря развитию математической теории экспериментов появилась возможность применения математических методов не только при обработке результатов наблюдений, но и при планировании экспериментального исследования. Планирование эксперимента – это постановка опытов по некоторой заранее составленной схеме, обладающей какими-то оптимальными свойствами. Разработка таких схем представляет собой сложную математическую задачу. В отличие от наиболее распространенного однофакторного метода исследований, когда изучается действие каждого фактора в отдельности, применение метода планирования эксперимента позволяет при исследовании сложных процессов выполнять эксперименты так, чтобы варьировать все факторы сразу. Это способствует повышению эффективности эксперимента, выражающейся в том, что интересующие экспериментатора параметры определяются со значительно меньшей ошибкой, чем при традиционных методах исследования. При этом с повышением числа факторов повышается точность эксперимента. При планировании эксперимента должны быть определены: необходимое число опытов, последовательность проведения эксперимента, математическая модель для описания эксперимента. При составлении плана проведения экспериментального исследования для каждой независимой переменной выбирается определенное число уровней варьирования. Поэтому необходимое число опытов определяется числом возможных комбинаций уровней варьирования независимых переменных, а также количеством повторных опытов.
Для планируемого эксперимента важную роль играет последовательность выполнения опытов. В целях усреднения эффектов от неконтролируемых переменных, сопутствующих любому экспериментальному исследованию (например, от изменения напряжения в сети, неоднородности обрабатываемого материала и материала режущего инструмента и т.д.) отдельные опыты следует проводить в случайной последовательности, которая может быть определена, например, с помощью таблиц случайных чисел, лотереи, путем бросания игральной кости или других способов. Сложнее решается вопрос выбора математической модели, описывающей эксперимент. В наиболее общем случае исследуемый процесс можно изобразить в виде некоторого «черного ящика».
Рис. 2. Представление процесса в виде «черного ящика»,
Необходимо выбрать модель процесса. Это уравнение, связывающее выход с факторами
Функцию (2.1) называют функцией отклика. Выбор связан с утверждением о возможности представления любой аналитической функции в виде полинома. Например, для двух факторов можно выбрать полином первой степени
второй степени
где Полиномы (2.2), (2.3) называют уравнениями регрессии. Коэффициенты полинома определяются экспериментом. Важный вопрос: какой выбрать полином на первом шаге? Если мы хотим получить интерполяционную модель, с помощью которой можно предсказать результат во всех точках выбранной области параметров. Целесообразно начинать с линейной модели. Если она окажется неадекватной, то следует увеличить степень полинома. Особенность решаемой задачи в том, что выражение (2.3) после его логарифмирования позволяет выбрать линейную модель полинома. Рассмотрим применение метода планирования эксперимента для исследования зависимости силы резания
где После логарифмирования выражения (2.4) получим линейную модель исследуемого процесса
где Теперь только останется разумно построить эксперимент, чтобы определить коэффициенты уравнения (2.3). Теперь только остается разумно построить эксперимент, чтобы определить коэффициенты уравнения (2.5). Далее для достижения поставленной цели будем действовать по следующему плану. 1. Выбор интервалов варьирования факторов. 2. Составление плана эксперимента и его проведения. 3. Вычисление коэффициентов уравнения регрессии и получение зависимости для определения силы резания. 1. Общие требования к факторам: управляемость и однозначность. Требования к совокупности факторов: совместимость и отсутствие линейной зависимости. Эти требования для выбранных факторов удовлетворяются. Теперь рассмотрим дальнейшие шаги, которые надо выполнить в общем случае. Поскольку выбранная модель линейна, то для каждого фактора необходимо выбрать два уровня, на которых он будет варьироваться. Один из этих уровней называют верхним, другой – нижним. Между этими двумя уровнями находится так называемый основной уровень. Введем еще одно понятие: интервал варьирования. Это некоторое число (свое для каждого фактора), прибавление которого к основному уровню дает верхний, а вычисление – нижний уровни. Интервал варьирования не может быть меньше той ошибки, с которой фиксируется уровень фактора. С другой стороны он не должен выходить за область определения фактора. Иногда выбор интервалов варьирования связан с интуитивными решениями, основанными на опыте экспериментатора. Так или иначе, выбор интервалов варьирования скажется на адекватности выбранной модели процесса. В данной работе интервалы варьирования определяются сравнительно узким диапазоном измерения факторов. Для упрощения записи плана эксперимента и обработки его результатов факторы кодируются. При этом верхнему уровню соответствует код «
где 2. План эксперимента строится на варьировании каждого фактора на двух уровнях. Все возможные комбинации уровней (число опытов N) определяются зависимостью N = 2 k, где 2 – это число уровней; 3. При расчете коэффициентов
где С помощью этой формулы определим для примера коэффициент
Рассмотрим пример.Пусть элемент режима резания меняются в пределах:
Вследствие симметричности плана эксперимента второе слагаемое в правой части равно 1. Поэтому окончательно получим
Аналогичным образом получим
Для принятых диапазонов изменения выражения (13) - (15) примут вид
Матрица планирования вместе с матрицей исходных данных и результатами экспериментов приведены в табл. 2. По выражению (2.10) определяем коэффициенты уравнения регрессии Вопросы для самопроверки 1. Какие различают два вида зависимостей между явлениями и процессами 2. Определите понятие планирование эксперимента. 3. Какую модель использует метод наименьших квадратов и как она связана с его названием? Каков алгоритм метода?
4. Что изучает дисциплина математическая статистика? 5. Перечислите простейшие характеристики распределения случайной величины. 6. Поясните понятия корреляция и регрессия. 7. Что означает термин «черный ящик»? 8. Что называют «функция отклика»? 9. Что должно быть определено при планировании эксперимента? 10. Что называется полным факторным экспериментом? 11. Что является геометрической интерпретацией полного факторного эксперимента? 12. Чему равно число комбинаций факторов в трехфакторном эксперименте 13. Напишите уравнение регрессии для двухфакторного эксперимента. 14. Что такое интервал варьирования? 15. Что такое нормированные факторы? 16. Назовите требования к факторам и требования к совокупности факторов. Вопросы для самопроверки 1. Дайте определение множества. 2. Как задать множество? 3. Что такое пустое множество? 4. Как обозначить объединение множеств? 5. Как записывается условие несовместимости событий? 6. Как записывается полная группа событий 7. Назовите виды статистических распределений. 8. Назовите основные числовые характеристики статистической выборки. 9. Назовите числовые характеристики выборочного распределения. 10. Что такое полигон распределения? 11. Что такое гистограмма распределения? 12. Что такое генеральная совокупность? 13. Что такое математическое ожидание? Показатели надежности
Показатели надежности можно разделить на две категории: единичные, которые характеризуют лишь одно свойство, например, только безотказность или только долговечность; комплексные, характеризующие несколько свойств. 1. Вероятность безотказной работы (ВБР) Безотказность –свойство объекта непрерывно сохранять работоспособное состояние в течение некоторого времени или наработки. Чем реже отказы в работе, тем выше безотказность. Согласно определению, основным показателем безотказности является вероятность Р того, что машина после включения проработает безотказно некоторое время.Так, Р (50) = 0,8 означает: вероятность того, что машина проработает 50 мин после включения, составляет 80 %. Простейшие испытания приборов на безотказность заключаются, например, в том, что 100 приборов ставятся параллельно на испытания и включаются в работу, после чего через желаемые промежутки времени определяется число отказавших и продолжающих работать. В упомянутом случае через 50 мин 20 приборов уже отказали (в любом интервале времени от 0 до 50 мин), а 80 продолжают работать, т.е. их отказы наступят после 50 мин. Безусловно, вероятность безотказной работы Р зависит от времени t. Функциональная зависимость вероятности Р (t)получила наименование «функция надежности» (правильно было бы назвать «функция безотказности», но термин утвердился). Это первый из показателей безотказности. Этот показатель определяется в предположении, что в начальный период времени объект находился в исправном состоянии. Функция (ВБР) обладает следующими свойствами 1. 0 ≤ Р (t) ≤ 1. 2. Функция Р (t) есть невозрастающая функция своего аргумента, т.е. если t 2 > t 1, то Р (t 2) ≤ Р (t 1). Некоторые характеристики этой функции: 1) Р (0) = 1, т.е. любое техническое средство должно включаться в 2) Р (∞)= 0, т.е. любое техническое средство рано или поздно будет В авиационной технике Р (t) = 0,9999 и выше. Если последствия отказа незначительны, а восстановление не связано с сверхнормативными затратами, то Р (t) ≤ 0,9. Приближенная оценка вероятности Р (t) по результатам испытаний может быть осуществлена с помощью формулы Вероятность того, что отказ объекта произойдет за время, не превышающее заданной величины t, то есть t < T, равна Q (t) = Q { T < t } = 1 – P (t), t ≥ 0. Функция Q (t) представляет собой интегральную функцию распределения случайной величины – времени отказа. Если функция Q (t) дифференцируема, то ее производная есть дифференциальный закон (плотность) распределения случайной величины – времени исправной работы. Некоторые общие свойства функции распределения Q (t), которые противоположны свойствам функции распределения ВБР Р (t). 1. 0 ≤ Q (t) ≤ 1. 2. Функция распределения Q (t) есть неубывающая функция своего аргумента, то есть при t 2 > t 1, Q (t 2) > Q (t 1). 3. В начальный момент времени функции распределения равна нулю: Q (0) = 0, и Q (∞)= 1. Графики функций Р (t), Q (t) представлены на рисунке.
Рис. 4.1 График функций: 1 – вероятности безотказной работы, 2 – вероятности отказа, 3 – плотности вероятности отказа
В теории надежности принято пользоваться понятием потока событий. Под потоком событий понимается такая последовательность событий, при которой они происходят одно за другим в случайные моменты времени. Основными потоками событий в теории надежности, являются потоки отказов и восстановлений. В теории надежности обычно используется формула Величина Средняя наработка до отказа (или математическое ожидание) – это момент первого порядка наработки объекта до первого отказа. Эту величину обычно обозначают T ср. и называют средним временем безотказной работы
где tj – время исправной работы j –го объекта. Средняя наработка на отказ – отношение наработки восстанавливаемого объекта к математическому ожиданию числа его отказов в течение этой наработки. Интенсивность потока отказов (или плотность) – среднее число отказов в единицу времени: Тогда интенсивность потока отказов, ч Значения Для ремонтопригодных систем высокой надежности характерна повышенная интенсивность отказов
Рис. 4.2 Характер изменения интенсивности отказов
Оценки долговечности технических систем Долговечность – свойство объекта сохранять работоспособное состояние до предельного состояния с необходимыми перерывами для технического обслуживания и ремонтов. Показатели долговечности технической системы отражают ее наработку до предельного состояния, не допустимого по техническим условиям, и календарную продолжительность эксплуатации системы до момента возникновения предельного состояния. Важнейший показатель долговечности – технический ресурс R – суммарное время от начала эксплуатации до предельного состояния
Технический ресурс деталей, сопряжений, механизмов и устройств оценивается по физическому износу, предельное состояние означает невозможность дальнейшей эксплуатации, после чего должен следовать восстановительный ремонт, либо замена. Время эксплуатации технической системы с учетом простоев, затрат времени на техническое обслуживание и т.д., называют сроком службы. Оценка ремонтопригодности технической системы Ремонтопригодность – свойство, заключающееся в приспособленности к поддержанию и восстановлению работоспособного состояния путем технического обслуживания и ремонта. Чем меньше время обнаружения и устранения отказов, тем выше ремонтопригодность. Длительность простоев для обнаружения и устранения отказов является такой же случайной величиной, как и длительность безотказной работы. Ремонтопригодность технической системы связана со временем Сохраняемость – свойство объекта сохранять свои эксплуатационные показатели в течение срока хранения и транспортировки. Резервирование систем Системы с позиции надежности могут быть последовательными, параллельными и комбинированными. В последовательных системах потеря работоспособности любого технического объекта приводит к отказу всей системы. В системах с параллельным соединением технических объектов отказ одного из них не приводит к отказу всей системы. Например, трехэкскалаторный подъем на станциях метро. К параллельным системам относятся так называемые системы с резервированием. В это понятие включается структурное резервирование, которое достига
|
|||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 106; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.87.167 (0.019 с.) |


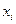 – входной параметр процесса (фактор),
– входной параметр процесса (фактор), 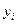 – выходной параметр процесса (выход, целевая функция).
– выходной параметр процесса (выход, целевая функция).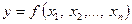 . (2.1)
. (2.1)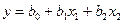 , (2.2)
, (2.2) , и т.д. (2.3)
, и т.д. (2.3)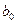 ,
, 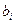 ,
, 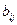 – коэффициенты полинома.
– коэффициенты полинома.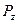 от режимов резания (
от режимов резания (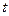 ,
, 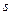 ,
, 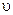 ). Особенность решения такой задачи в том, что многочисленные исследования показали возможность аппроксимации этой зависимости в виде степенной функции, которая при многофакторном эксперименте имеет вид
). Особенность решения такой задачи в том, что многочисленные исследования показали возможность аппроксимации этой зависимости в виде степенной функции, которая при многофакторном эксперименте имеет вид , (2.4)
, (2.4)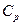 ,
, 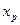 ,
, 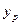 ,
, 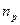 – коэффициенты, подлежащие экспериментальному определению.
– коэффициенты, подлежащие экспериментальному определению.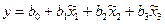 , (2.5)
, (2.5)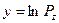 ;
; 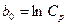 ;
; 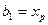 ;
; 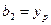 ;
; 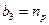 ;
; 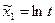 ;
; 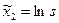 ;
; 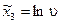 .
.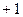 », а нижнему – «
», а нижнему – «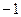 », а основному «
», а основному «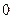 ». Этого можно добиться с помощью преобразования
». Этого можно добиться с помощью преобразования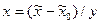 , (2.6)
, (2.6)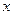 – кодированное значение фактора;
– кодированное значение фактора; 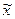 – натуральное значение фактора;
– натуральное значение фактора; 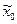 – натуральное значение основного (нулевого) уровня;
– натуральное значение основного (нулевого) уровня; 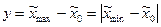 – натуральное значение интервала варьирования;
– натуральное значение интервала варьирования; 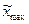 ,
, 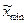 – соответственно натуральные значения верхнего и нижнего уровней.
– соответственно натуральные значения верхнего и нижнего уровней.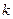 – число факторов. В нашем случае N = 23 = 8. Эксперимент, в котором реализуются все возможные сочетания уровней факторов, называется полным факторным экспериментом (ПФЭ). Каждый столбец в этой матрице называется вектор столбцом, а каждая строка вектор-столбцом. Геометрической интерпретацией эксперимента 23 является куб. Этот куб задает область эксперимента, а центр куба определяет основной (нулевой) уровень. После некоторых рассуждений матрица планирования претерпит некоторые изменения. Они связаны с процедурой расчета коэффициентов уравнения регрессии.
– число факторов. В нашем случае N = 23 = 8. Эксперимент, в котором реализуются все возможные сочетания уровней факторов, называется полным факторным экспериментом (ПФЭ). Каждый столбец в этой матрице называется вектор столбцом, а каждая строка вектор-столбцом. Геометрической интерпретацией эксперимента 23 является куб. Этот куб задает область эксперимента, а центр куба определяет основной (нулевой) уровень. После некоторых рассуждений матрица планирования претерпит некоторые изменения. Они связаны с процедурой расчета коэффициентов уравнения регрессии.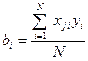 , (2.7)
, (2.7)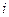 » опыте;
» опыте; 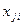 – значение «
– значение «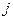 » фактора в «
» фактора в «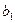 . То есть для подсчета оценки коэффициента
. То есть для подсчета оценки коэффициента 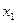 . Для вычисления
. Для вычисления 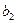 ,
, 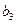 потребуются вектор-столбцы
потребуются вектор-столбцы  ,
, 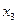 . Как найти
. Как найти 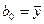 , то есть
, то есть 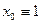 , а в матрицу планирования введем дополнительно вектор-столбец
, а в матрицу планирования введем дополнительно вектор-столбец 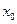 . При этом добавим два эксперимента в центре плана. В итоге получим
. При этом добавим два эксперимента в центре плана. В итоге получим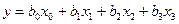 . (2.8)
. (2.8)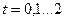 мм;
мм; 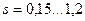 мм/об;
мм/об; 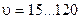 м/мин. В соответствии с уравнением (8) и выражением (9) определим кодовые значения факторов.
м/мин. В соответствии с уравнением (8) и выражением (9) определим кодовые значения факторов.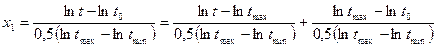 .
.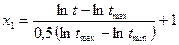 . (2.9)
. (2.9)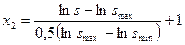 . (2.10)
. (2.10)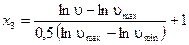 . (2.11)
. (2.11)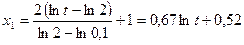 ;
;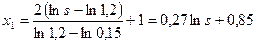 ;
;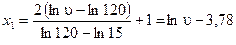 .
.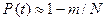 , где m – число отказавших систем, N – общее число испытанных систем.
, где m – число отказавших систем, N – общее число испытанных систем.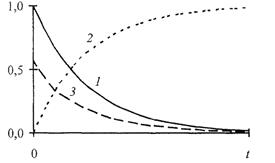
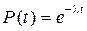 , где е – основание натуральных логарифмов,
, где е – основание натуральных логарифмов, 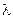 – параметр потока отказов как характеристика их интенсивности.
– параметр потока отказов как характеристика их интенсивности.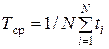 ,
,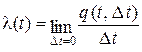 , где
, где 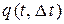 – вероятность отказа за период
– вероятность отказа за период 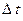 . Приближенно можно принять
. Приближенно можно принять 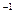 :
: 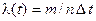 .
.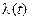 для различных типов систем определяются опытным путем (по специальным методикам испытаний) и заносятся в справочные таблицы. Примерное распределение отказов по видам: 48% – электронное и электрическое оборудование, 37% – механические узлы, 15% – гидро- и пневмоприводы.
для различных типов систем определяются опытным путем (по специальным методикам испытаний) и заносятся в справочные таблицы. Примерное распределение отказов по видам: 48% – электронное и электрическое оборудование, 37% – механические узлы, 15% – гидро- и пневмоприводы.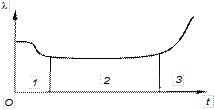
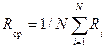 .
.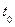 проведения плановых ремонтов при восстановлении работоспособности технической систем; можно оценить вероятностью выполнения ремонта в заданное время вне зависимости от сложности отказа по формуле:
проведения плановых ремонтов при восстановлении работоспособности технической систем; можно оценить вероятностью выполнения ремонта в заданное время вне зависимости от сложности отказа по формуле: 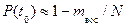 , где
, где 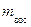 – число восстановленных систем за время
– число восстановленных систем за время 


