
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение задачи графическим способомСодержание книги
Поиск на нашем сайте
Для определения режимов резания для двух элементов s и n широко применяется метод линейного программирования, общая задача которого состоит в определении неотрицательных значений переменных, удовлетворяющих системе ограничений в виде линейных равенств и неравенств и обеспечивающих наибольшее и наименьшее значение некоторой линейной функции – критерия оптимальности. Таким образом, первая задача – приведение всех технических ограничений и оценочной функции к линейному виду. Имеем скорость резания для различных видов обработки
где Рассмотрим приведение к линейному виду для технического ограничения по режущим возможностям инструмента методом логарифмирования:
Введем обозначения
подставим их в неравенство и получим
Аналогично могут быть получены в линейном виде зависимости и для других ограничений. Математическую модель процесса резания можно изобразить в графическом виде. При этом каждое техническое ограничение представляется граничной прямой, которая определяет полуплоскость, где возможно существование решений системы неравенств. Граничные переменные, пересекаясь, образуют многоугольник АВС DEF, внутри которого любая точка удовлетворяет всем без исключения неравенствам системы, поэтому этот многоугольник называют многоугольником решений.
Рис. 7.1 Графическое изображение математической модели процесса резания
Теория линейного программирования показывает, что экстремальное значение оценочной функции (при выпуклом многоугольнике решений) обеспечивается для Вопросы для самопроверки 1. В чем суть оптимизационной задачи? 2. Что представляет собой теория оптимизации? 3. В чем состоит ценность теории оптимизации? 4. Назовите важнейший момент теории оптимизации 5. Выбор критерия оптимизации 6. Что представляет собой целевая функция? 7. Основная задача линейного программирования? 8. Какие этапы оптимизации можно выделить при проектировании технических объектов? 9. Что понимается под термином «оптимальное решение»? 10. Какие существуют виды критериев оптимальности технологических процессов? 11. Какие основные требования к критериям оптимальности технологических процессов? 12. Какие методы оптимизации используются при технологическом проектировании? 13. В чем сущность структурной и параметрической оптимизации? 14. Как графически изображается математическая модель при оптимизации режимов резания? 15. Чем ограничиваются режущие возможности инструмента и как они учитываются при оптимизации режимов резания?
|
||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 154; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.1.100 (0.009 с.) |

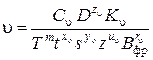
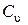 – постоянный коэффициент, характеризующий нормативные условия обработки; D – диаметр обрабатываемой детали;
– постоянный коэффициент, характеризующий нормативные условия обработки; D – диаметр обрабатываемой детали; 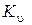 – поправочный коэффициент, учитывающий качество обрабатываемого материала, состояние поверхности заготовки и характеристику режущего инструмента; Т – принятая стойкость инструмента, мин; m – показатель относительной стойкости; t – глубина резания, мм; s – подача, мм/об; z – число зубьев режущего инструмента;
– поправочный коэффициент, учитывающий качество обрабатываемого материала, состояние поверхности заготовки и характеристику режущего инструмента; Т – принятая стойкость инструмента, мин; m – показатель относительной стойкости; t – глубина резания, мм; s – подача, мм/об; z – число зубьев режущего инструмента; 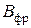 – ширина фрезерования;
– ширина фрезерования; 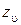 ,
, 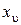 ,
, 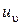 ,
, 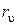 – показатели степеней.
– показатели степеней.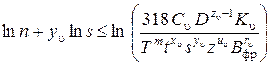 .
.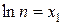 ,
,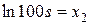 ,
,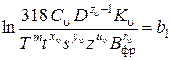 ,
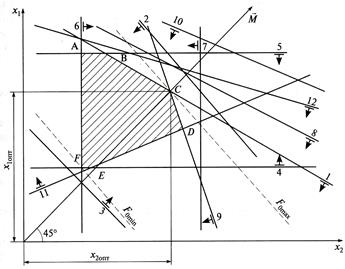
,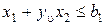 .
.
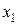 и
и 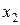 , находящихся в точке, лежащей на одной из граничных прямых или их пересечении. Поэтому задача отыскания оптимальных значений
, находящихся в точке, лежащей на одной из граничных прямых или их пересечении. Поэтому задача отыскания оптимальных значений 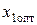 и
и  сводится к последовательному вычислению координат всех возможных точек пересечения граничных прямых, а затем к определению для них максимального значения суммы
сводится к последовательному вычислению координат всех возможных точек пересечения граничных прямых, а затем к определению для них максимального значения суммы 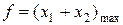 .
.


