
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод Гаусса нахождения ранга матрицыСодержание книги
Поиск на нашем сайте
Пусть дана матрица
1. Привести матрицу к ступенчатому виду (см. метод Гаусса).
2. В полученной матрице вычислить количество
Замечания 3.5.
1. Обоснованием этого метода служит следствие 2 теоремы 3.4. Базисным минором в матрице ступенчатого вида (см. рис. 1.4) является минор
2. Метод Гаусса для нахождения ранга произвольной матрицы наиболее экономичен, так как требует меньше вычислений, чем другие методы. Конечно, для матриц какого-либо специального вида (блочных, разреженных и т.п.) можно предложить более эффективные методы.
Пример 3.7. Методом Гаусса найти ранги матриц
Решение. Матрица
2. Количество ненулевых строк равно нулю. Следовательно,
Матрица
2. В этой матрице две ненулевые строки. Следовательно,
Матрица
В этой матрице две ненулевые строки. Следовательно,
Матрица
У которой имеются две равные строки. По следствию 1 теоремы 3.3 одну из равных строк вычеркиваем:
Получили матрицу ступенчатого вида (см. п. 1 замечаний 1.8).
2. В этой матрице две ненулевые строки. Следовательно,
Матрица
Последние три строки матрицы пропорциональны. По следствию 1 теоремы 3.3 две из них можно вычеркнуть:
Получили матрицу ступенчатого вида (см. п. 1 замечаний 1.8).
2. В этой матрице две ненулевые строки. Следовательно,
Заметим, что
Пример 3.8. Даны матрицы
Найти ранги матриц:
Решение. По определению имеем
Билет 12 Теорема Кронекера – Капелли Линейной системой m уравнений с n неизвестными
где Решением ЛСУ называется такая упорядоченная совокупность чисел Совместная система называется определенной, если она имеет единственное решение и неопределенной, если имеет бесконечное множество решений. Чтобы решить систему, сначала надо выяснить, совместна ли она. Для ответа на этот вопрос введем матричную запись ЛСУ. Матрица
составленная из коэффициентов при неизвестных ЛСУ, называется основной матрицей системы, а матрица
которая получается добавлением в матрицу А столбца из свободных членов, называется расширенной матрицей ЛСУ. Введем также матрицы-столбцы
где X и В – матрицы неизвестных и свободных членов. Тогда, используя правило умножения матриц и определение равенства двух матриц, запишем ЛСУ в матричном виде:
Теорема Кронекера – Капелли. Для совместности системы линейных уравнений необходимо и достаточно, чтобы r(A) = 1) 2) r < n, то система не определена и имеет бесконечное множество решений. Пример 7. Данасистема линейных уравнений: Записать приведенную систему в матричном виде и исследовать ее на совместность. Решение. Введем основную и расширенную матрицы системы:
Для вычисления r(А) и Столбец из свободных членов в Выполняя элементарные преобразования над матрицей
|
||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 185; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.59.124 (0.009 с.) |

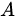 размеров
размеров  . Для нахождения ее ранга нужно выполнить следующие действия.
. Для нахождения ее ранга нужно выполнить следующие действия. ненулевых строк. Это число равно рангу матрицы
ненулевых строк. Это число равно рангу матрицы 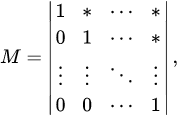
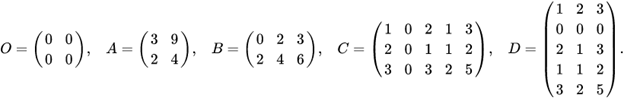
 . 1. Нулевая матрица уже имеет ступенчатый вид (см. п.2 замечаний 1.8).
. 1. Нулевая матрица уже имеет ступенчатый вид (см. п.2 замечаний 1.8).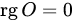 .
.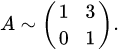
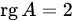 .
. . 1. Приводим матрицу
. 1. Приводим матрицу 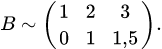
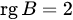 .
. . 1. Приводим матрицу
. 1. Приводим матрицу  , делаем равными нулю остальные элементы первого столбца: ко второй строке прибавляем первую, умноженную на (-2), к третьей строке — первую, умноженную на (-3). Получаем матрицу
, делаем равными нулю остальные элементы первого столбца: ко второй строке прибавляем первую, умноженную на (-2), к третьей строке — первую, умноженную на (-3). Получаем матрицу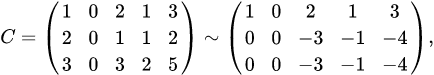
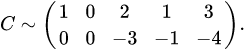
 .
.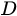 . 1. Приводим матрицу
. 1. Приводим матрицу 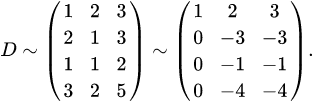
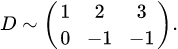
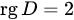 .
. , так как
, так как  (см. следствие 1 теоремы 3.4).
(см. следствие 1 теоремы 3.4).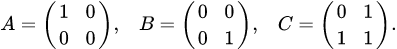
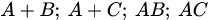 .
.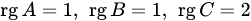 . Находим суммы и произведения данных матриц, а также их ранги:
. Находим суммы и произведения данных матриц, а также их ранги: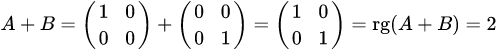 , то есть
, то есть 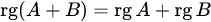 ;
;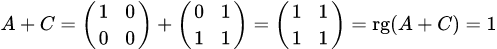 , то есть
, то есть 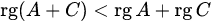 ;
;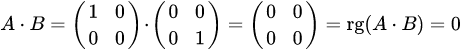 , то есть
, то есть  ;
;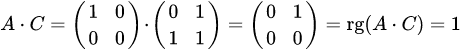 , то есть
, то есть  ;
;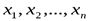 (ЛСУ) называется система вида
(ЛСУ) называется система вида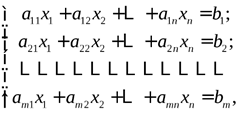 (2.7)
(2.7)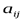 – коэффициент (число) при неизвестном
– коэффициент (число) при неизвестном 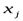 в i -м уравнении;
в i -м уравнении; 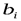 – свободный член в этом уравнении,
– свободный член в этом уравнении, 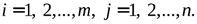
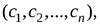 что при подстановке вместо
что при подстановке вместо 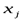 соответственно
соответственно 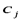 в каждое уравнение системы все уравнения обращаются в верные равенства. ЛСУ называется совместной, если существует хотя бы одно решение системы (одна совокупность
в каждое уравнение системы все уравнения обращаются в верные равенства. ЛСУ называется совместной, если существует хотя бы одно решение системы (одна совокупность 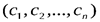 ), в противном случае – несовместной.
), в противном случае – несовместной. (2.8)
(2.8) (2.9)
(2.9)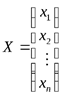
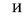
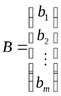 ,(2.10)
,(2.10)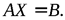 (2.11)
(2.11)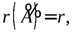 при этом, если
при этом, если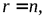 то система определена и имеет единственное решение;
то система определена и имеет единственное решение;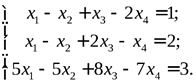
 ;
;  , матрицы-столбцы
, матрицы-столбцы 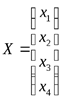 ;
; 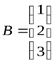 , тогда система запишется в виде матричного уравнения:
, тогда система запишется в виде матричного уравнения: 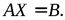
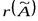 выполним элементарные преобразования над матрицей
выполним элементарные преобразования над матрицей 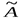 , так как матрица А является частью матрицы
, так как матрица А является частью матрицы 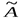 и
и 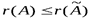 .
.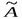 отделим вертикальной чертой и в процессе преобразований не будем его менять местами с другими столбцами матрицы А.
отделим вертикальной чертой и в процессе преобразований не будем его менять местами с другими столбцами матрицы А. описанные в подразд. 1.5, получаем:
описанные в подразд. 1.5, получаем:
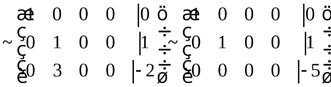
 следовательно, r(A) = 2, r(
следовательно, r(A) = 2, r( ) = 3 и система несовместна, т. е. не имеет решений.
) = 3 и система несовместна, т. е. не имеет решений.


