
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Умножение матриц. Транспонирование. Свойства.Стр 1 из 10Следующая ⇒
Билет 1 1. Матрицы. Линейные операции над ними и их свойства. Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины.
Матрицы равны между собой, если равны все их соответствующие элементы. Матрица, у которой число строк и столбцов равно – называется квадратной. Матрица, все элементы которой, кроме элементов главной диагонали равны нулю, называется диагональной. Диагональная матрица, у которой все элементы главной диагонали равны 1, называется единичной. Обозначается буквой Е. Матрица, у которой все элементы по одну сторону от главной диагонали равны нулю, называется треугольной. Матрица, у которой все элементы равны нулю, называется нулевой. Билет 2 Умножение матриц. Транспонирование. Свойства. Операция умножения возможна, если количество столбцов первой матрицы равно количеству строк другой матрицы.
где 1. 2. 3. 4. Матрица, полученная заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной, к данной. 1. 2. Билет 3,4 Определители матриц. Свойства определителей. Миноры и алгебраические дополнения. 1. 2. 3.
Свойства: 1. Определитель не изменится, если его строки заменить столбцами, и наоборот. 2. При перестановке двух параллельных рядов определитель меняет знак. 3. Определитель, имеющий два одинаковых или пропорциональных ряда, равен нулю. 4. Общий множитель элементов можно вынести за знак определителя. 5. Если элементы какого-либо ряда представляют собой сумму элементов, то определитель может быть разложен на сумму двух соответствующих определителей. 6. Определитель не изменится, если прибавим ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и тоже число. 7. Определитель равен сумме элементов, умноженных на соответствующее им алгебраическое дополнение. 8. Сумма произведения элементов одного ряда на алгебраические дополнения параллельного ряда равна нулю. Разложение определителя по элементам ряда. Теорема замещения. Определитель равен сумме произведений элементов на соответствующее им алгебраическое дополнение.
Берем любые N чисел
Билет Определители второго, третьего, n-го порядка Билет Обратная матрица. Достаточное условие существования обратной матрицы.
1. 2. 3. Для того чтобы матрица имела обратную достаточно того, чтобы она была невырождена. Билет Билет Доказательство. Так как система векторов Добавим к исходной системе векторов еще s векторов 2. Если из линейно независимой системы векторов Доказательство. Предположим, что полученная система линейно зависима. Добавив к этой системе векторов все отброшенные векторы, мы получим исходную систему векторов. По условию – она линейно независима, а в силу предыдущего свойства линейной зависимости она должна быть линейно зависимой. Мы пришли к противоречию, следовательно, наше предположение неверно. 3. Если в системе векторов Доказательство. Пусть вектор 4. Если система векторов Доказательство. Сначала докажем первое утверждение.
Пусть система векторов Теперь докажем второе утверждение. Так как система векторов Предположим, что какой-нибудь вектор системы Из двух последних свойств следует важное утверждение: К началу страницы Билет Система векторов 1. Все базисы состоят из одного и того же числа векторов. Если число векторов в базисе линейного пространства L равно 2. Всякая система из 3. Всякая линейно независимая система векторов 4. Всякую линейно независимую систему векторов 5. Если Пример 1. Доказать, что многочлены Решение. Система многочленов
Действительно, Пример 2. Доказать, что матрицы Решение. Согласно определению нужно доказать, что система векторов E1, E2, E3, E4 линейно независима и любая матрица из M2 является их линейной комбинацией. Система E1, E2, E3, E4линейно независима. Так как произвольная матрица Координаты вектора Пример 3. Пусть е1,…,еn базис пространства L. Каждому вектору х L поставим в соответствие строку его координат хе в этом базисе 1) векторы 2) если вектор u линейно выражается через систему 3) ранг системы векторов Замечание 1. Приведённые утверждения в примере 3 можно сформулировать и для столбцов, т. е. если каждому вектору х L поставить в соответствие столбец его координат хе в этом базисе Замечание 2. Понятие базиса системы векторов и ее ранга вводится аналогично. Если Пример 4. Найти базис и ранг системы многочленов Решение. Согласно приведённым в предыдущей задаче утверждениям составим матрицу, строки которой являются координатными строками данных многочленов. Так как эта матрица имеет вид
Пример 5. Показать, что в линейном Решение. Пусть
Так как эта матрица квадратная и ее строки линейно независимы, то Проводя рассуждения в обратном порядке, мы приходим к следующему заключению: если определитель порядка Пример 6. Доказать, что многочлены Решение. Составим определитель из координатных строк этих векторов
Так как этот определитель отличен от нуля, то система векторов
Решая систему, получаем Билет 10 Рассмотрим матрицу
Выделим в ней k-строк и k-столбцов (k≤(min(m,n))). Из элементов, стоящих на пересечении выделенных строк и столбцов, составим определитель k-го порядка. Все такие определители называются минорами этой матрицы. Рассмотрим всевозможные миноры матрицы А, отличные от нуля. Рангом матрицы А называется наибольший порядок минора этой матрицы, отличного от нуля. Если все элементы матрицы равны нулю, то ранг этой матрицы принимают равным нулю. Минор, порядок которого определяет ранг матрицы, называется базисным. У матрицы может быть несколько базисных миноров. Ранг матрицы А обозначается r(A). Если r(A)=r(B), то матрицы А и В называются эквивалентными. Пишут A ̴ ∼ В. Свойства ранга матрицы:
Под элементарными преобразованиями понимают:
При вычислении ранга матрицы могут быть использованы элементарные преобразования, метод приведения матрицы к ступенчатому виду, метод окаймляющих миноров. Метод приведения матрицы к ступенчатому виду заключается в том, что при помощи элементарных преобразований данная матрица приводится к ступенчатой. Матрица называется ступенчатой, если в каждой ее строке первый ненулевой элемент стоит правее, чем в предыдущей (т. е. получаются ступеньки, высота каждой ступеньки должна быть равна единице). Примеры ступенчатых матриц:
Примеры не ступенчатых матриц:
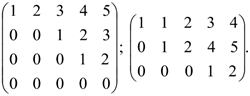
ПРИМЕР: Найти ранг матрицы:
РЕШЕНИЕ: Приведем данную матрицу к ступенчатой с помощью элементарных преобразований. 1.Поменяем местами первую и третью строки.
2. Получим в первом столбце нули под единицей. Прибавив ко второй строке первую, умноженную на (-3), к третьей – первую, умноженную на (-5), к четвертой – первую, умноженную на (-3), получим
Для того чтобы было понятней где еще нужно получить нули, нарисуем ступеньки в матрице. (Матрица будет ступенчатой, если везде под ступеньками будут нули)
3. Прибавив к третьей строке вторую, умноженную на (-1), к четвертой – вторую, умноженную на (-1), получим нули под ступеньками во втором столбце.
Если нарисовать опять ступеньки, увидим, что матрица ступенчатая.
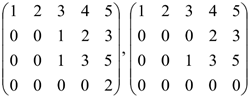
Ее ранг равен r=3 (число строк ступенчатой матрицы, в каждой из которых хотя бы один элемент отличен от нуля). Следовательно, ранг данной матрицы r=3. Решение можно записать так:
(римскими цифрами обозначены номера строк) Ответ: r=3. Минор порядка k+1, содержащий в себе минор порядка k называется окаймляющим минор. Метод окаймляющих миноров основан на том, что ранг данной матрицы равен порядку такого минора этой матрицы, который отличен от нуля, а все окаймляющие его миноры равны нулю. ПРИМЕР: Найти ранг матрицы:
РЕШЕНИЕ: Найдем теперь ранг этой матрицы методом окаймляющих миноров. Среди миноров первого порядка есть отличные от нуля, например 5. Среди окаймляющих его миноров есть отличный от нуля, например
Среди миноров, окаймляющих этот минор, есть отличный от нуля, например
Так как единственный минор, окаймляющий последний минор равен нулю, то r=3.
Ответ: r=3. Билет 11 Метод окаймляющих миноров
Находить ранг матрицы по определению — вычисляя миноры всех порядков — очень трудоемкая операция. Следующий алгоритм позволяет уменьшить число рассматриваемых миноров.
Пусть дана матрица
1. Выбираем строку
2. Окаймляем минор
Если это возможно, то
3. Окаймляем минор
Продолжаем процесс окаймления, пока он не завершится. Пусть найден минор r-го порядка
Пример 3.6. Методом окаймляющих миноров найти ранги матриц
Решение. Матрица
Матрица
2. Добавляем к выбранным строке и столбцу еще одну строку
3. Поскольку исчерпаны все строки и все столбцы матрицы
Матрица
2. Добавляем к уже выбранным вторую строку и третий столбец. Получаем минор второго порядка
3. Все строки матрицы
Матрица
2. Добавляем к выбранным строке и столбцу еще одну строку
3. Окаймляем минор
Три определителя равны нулю, так как третья строка равна сумме первых двух строк. Следовательно, нельзя найти отличный от нуля окаймляющий минор 3-го порядка, т.е. ранг матрицы
Замечание 3.4. Метод окаймляющих миноров позволяет уменьшить по сравнению с определением количество рассматриваемых миноров. Если в матрице размеров
Замечания 3.5.
1. Обоснованием этого метода служит следствие 2 теоремы 3.4. Базисным минором в матрице ступенчатого вида (см. рис. 1.4) является минор
2. Метод Гаусса для нахождения ранга произвольной матрицы наиболее экономичен, так как требует меньше вычислений, чем другие методы. Конечно, для матриц какого-либо специального вида (блочных, разреженных и т.п.) можно предложить более эффективные методы.
Пример 3.7. Методом Гаусса найти ранги матриц
Решение. Матрица
2. Количество ненулевых строк равно нулю. Следовательно,
Матрица
2. В этой матрице две ненулевые строки. Следовательно,
Матрица
В этой матрице две ненулевые строки. Следовательно,
Матрица
У которой имеются две равные строки. По следствию 1 теоремы 3.3 одну из равных строк вычеркиваем:
Получили матрицу ступенчатого вида (см. п. 1 замечаний 1.8).
2. В этой матрице две ненулевые строки. Следовательно,
Матрица
Последние три строки матрицы пропорциональны. По следствию 1 теоремы 3.3 две из них можно вычеркнуть:
Получили матрицу ступенчатого вида (см. п. 1 замечаний 1.8).
2. В этой матрице две ненулевые строки. Следовательно,
Заметим, что
Пример 3.8. Даны матрицы
Найти ранги матриц:
Решение. По определению имеем
|
|||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 105; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.143.31 (0.323 с.) |


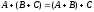

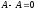
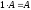




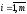

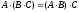

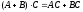


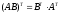
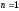







 Для нахождения определителя более высокого порядка, матрицу приводят к треугольному виду и считают произведение элементов на главной диагонали.
Для нахождения определителя более высокого порядка, матрицу приводят к треугольному виду и считают произведение элементов на главной диагонали. и умножим на алгебраическое дополнение какой-либо строки.
и умножим на алгебраическое дополнение какой-либо строки.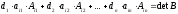


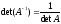


 линейно зависима, то равенство
линейно зависима, то равенство 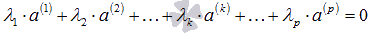 возможно при наличии хотя бы одного ненулевого числа из чисел
возможно при наличии хотя бы одного ненулевого числа из чисел  . Пусть
. Пусть  .
.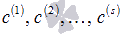 , при этом получим систему
, при этом получим систему 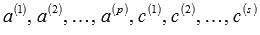 . Так как
. Так как  , то линейная комбинация векторов этой системы вида
, то линейная комбинация векторов этой системы вида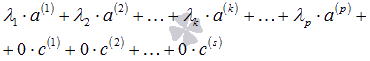
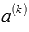 в этой системе векторов является нулевым. Предположим, что исходная система векторов линейно независима. Тогда векторное равенство
в этой системе векторов является нулевым. Предположим, что исходная система векторов линейно независима. Тогда векторное равенство  . Однако, если взять любое
. Однако, если взять любое  , отличное от нуля, то равенство
, отличное от нуля, то равенство  . Следовательно, наше предположение неверно, и исходная система векторов линейно зависима.
. Следовательно, наше предположение неверно, и исходная система векторов линейно зависима.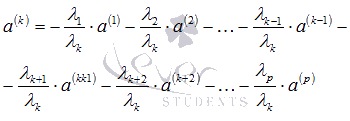
 возможно лишь при
возможно лишь при  , тогда
, тогда 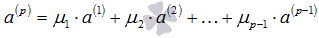 . Это равенство можно переписать как
. Это равенство можно переписать как  , в его левой части находится линейная комбинация векторов системы, причем коэффициент перед вектором
, в его левой части находится линейная комбинация векторов системы, причем коэффициент перед вектором 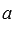 и
и 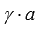 , где
, где  – произвольное число, то она линейно зависима.
– произвольное число, то она линейно зависима.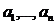 линейного пространства
линейного пространства  называется максимальной линейно независимой системой в
называется максимальной линейно независимой системой в 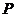 , то его нулевой вектор 0 сам составляет линейное пространство над полем
, то его нулевой вектор 0 сам составляет линейное пространство над полем  , то линейное пространство называется
, то линейное пространство называется 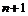 вектор, линейно зависима, любая линейно независимая система состоит не более чем из
вектор, линейно зависима, любая линейно независимая система состоит не более чем из 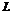 ,
,  , содержится в некотором базисе
, содержится в некотором базисе 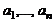 базис линейного пространства
базис линейного пространства 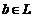 можно разложить по базису, т. е. представить в виде Это разложение для
можно разложить по базису, т. е. представить в виде Это разложение для  единственно. Коэффициенты
единственно. Коэффициенты 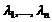 называются координатами вектора
называются координатами вектора 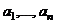 .
.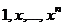 cоставляют базис пространства Pn(x) Указать размерность этого пространства и координаты многочлена а0+а1х+…+аnxn в этом базисе.
cоставляют базис пространства Pn(x) Указать размерность этого пространства и координаты многочлена а0+а1х+…+аnxn в этом базисе.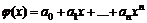 из Pn(x), то получим линейно зависимую систему, так как многочлен
из Pn(x), то получим линейно зависимую систему, так как многочлен 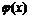 является линейной комбинацией многочленов
является линейной комбинацией многочленов  Следовательно, система многочленов
Следовательно, система многочленов 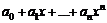 в этом базисе являются числа
в этом базисе являются числа  .
.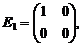

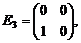
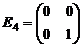 составляют базис линейного действительного пространства M2 матриц второго порядка Указать размерность пространства M2. Найти координаты вектора
составляют базис линейного действительного пространства M2 матриц второго порядка Указать размерность пространства M2. Найти координаты вектора 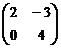 в этом базисе.
в этом базисе. может быть представлена в виде:
может быть представлена в виде: 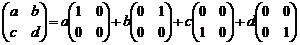 , то E1, E2, E3, E4 составляют базис пространства M2 и размерность его равна 4.
, то E1, E2, E3, E4 составляют базис пространства M2 и размерность его равна 4.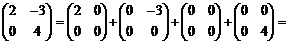
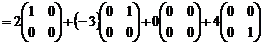 .
.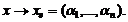 Тогда справедливы следующие утверждения:
Тогда справедливы следующие утверждения: тогда и только тогда линейно зависимы (независимы), когда их координатные строки
тогда и только тогда линейно зависимы (независимы), когда их координатные строки 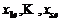 линейно зависимы (независимы);
линейно зависимы (независимы);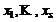 , т. е.
, т. е. 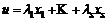 , то это же верно для строк
, то это же верно для строк  , причем
, причем 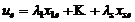 и обратно;
и обратно; равен рангу системы их строк
равен рангу системы их строк 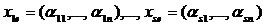 .
.
 – некоторая система векторов из L, то всякая ее максимальная линейно независимая подсистема называется базисом этой системы. Оказывается, все базисы системы векторов содержат одно и то же число векторов. Число векторов, составляющих базис системы векторов, называется ее рангом.
– некоторая система векторов из L, то всякая ее максимальная линейно независимая подсистема называется базисом этой системы. Оказывается, все базисы системы векторов содержат одно и то же число векторов. Число векторов, составляющих базис системы векторов, называется ее рангом.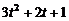 ,
, 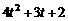 ,
, 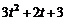 ,
, 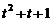 ,
, 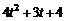 .
. и ее миноры
и ее миноры  ,
, 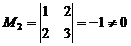 ,
,  , то ранг этой матрицы равен 3. Следовательно, ранг системы координатных строк, а потому и ранг системы многочленов равен 3. Один из базисов составляют те многочлены, координатные строки которых вошли в минор М3, т. е.
, то ранг этой матрицы равен 3. Следовательно, ранг системы координатных строк, а потому и ранг системы многочленов равен 3. Один из базисов составляют те многочлены, координатные строки которых вошли в минор М3, т. е. 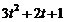 ,
,  ,
, 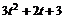 .
.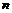 -мерном пространстве
-мерном пространстве  критерием линейной независимости
критерием линейной независимости 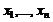 – векторы из
– векторы из 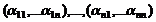 – их координатные строки. Составим матрицу
– их координатные строки. Составим матрицу .
.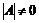 .
. составляют базис пространства
составляют базис пространства  . Найти координаты вектора 3х2−х−3 в этом базисе.
. Найти координаты вектора 3х2−х−3 в этом базисе.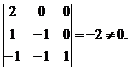
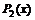 Найдем координаты вектора
Найдем координаты вектора 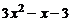 в этом базисе:
в этом базисе: 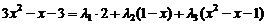 . Приравниваем коэффициенты при одинаковых степенях неизвестного
. Приравниваем коэффициенты при одинаковых степенях неизвестного
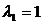 ,
, 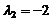 ,
,  – координаты многочлена
– координаты многочлена 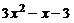 в базисе
в базисе 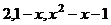 .
. .
.


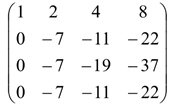





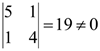

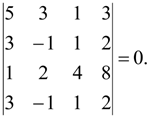
 размеров
размеров  . Будем говорить, что минор
. Будем говорить, что минор  (k+l)-ro порядка окаймляет (содержит в себе) минор
(k+l)-ro порядка окаймляет (содержит в себе) минор 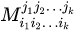 k-го порядка. При описании метода индексы выбранных строк и столбцов, в которых располагается минор, будем указывать, не упорядочивая их по возрастанию. При этом рассматриваемый минор и минор с упорядоченными индексами равны по абсолютной величине и, быть может, отличаются по знаку, но это для метода окаймляющих миноров не имеет никакого значения, поскольку нас интересует только ответ на вопрос: равен минор нулю или нет.
k-го порядка. При описании метода индексы выбранных строк и столбцов, в которых располагается минор, будем указывать, не упорядочивая их по возрастанию. При этом рассматриваемый минор и минор с упорядоченными индексами равны по абсолютной величине и, быть может, отличаются по знаку, но это для метода окаймляющих миноров не имеет никакого значения, поскольку нас интересует только ответ на вопрос: равен минор нулю или нет.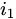 и столбец
и столбец 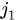 так, чтобы минор 1-го порядка
так, чтобы минор 1-го порядка  был не равен нулю. Если это возможно, то
был не равен нулю. Если это возможно, то  , иначе процесс завершается и
, иначе процесс завершается и 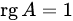 .
. , добавляя к выбранным
, добавляя к выбранным  и столбец
и столбец  так, чтобы минор
так, чтобы минор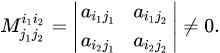
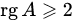 , иначе процесс завершается и
, иначе процесс завершается и 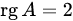 .
. , добавляя к выбранным ранее строкам и столбцам новую строку
, добавляя к выбранным ранее строкам и столбцам новую строку 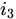 и новый столбец
и новый столбец 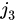 так, чтобы получить минор
так, чтобы получить минор 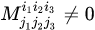 . Если это удалось, то
. Если это удалось, то 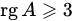 , иначе процесс завершается и
, иначе процесс завершается и 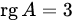 .
. , т.е.
, т.е. 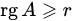 . Однако, все миноры (r+l)-ro порядка, окаймляющие его, равны нулю
. Однако, все миноры (r+l)-ro порядка, окаймляющие его, равны нулю 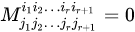 или не существуют (при
или не существуют (при  или
или  ). Тогда процесс завершается и
). Тогда процесс завершается и  .
.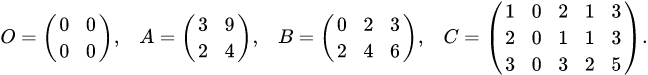
 . 1. В этой матрице нет отличных от нуля миноров первого порядка, так как все ее элементы равны нулю. Поэтому
. 1. В этой матрице нет отличных от нуля миноров первого порядка, так как все ее элементы равны нулю. Поэтому  .
.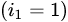 и первый столбец
и первый столбец  матрицы
матрицы 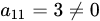 . Получили минор
. Получили минор 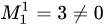 . Следовательно,
. Следовательно,  и еще один столбец
и еще один столбец  . Получаем отличный от нуля минор второго порядка
. Получаем отличный от нуля минор второго порядка Следовательно,
Следовательно,  , нет. Следовательно,
, нет. Следовательно,  . 1. Выбираем первую строку и второй столбец матрицы
. 1. Выбираем первую строку и второй столбец матрицы 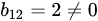 . Получили минор
. Получили минор 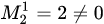 . Следовательно,
. Следовательно,  .
. . Выбор оказался неудачным, так как получили нулевой минор. Вместо третьего столбца возьмем первый. Тогда получим отличный от нуля минор второго порядка
. Выбор оказался неудачным, так как получили нулевой минор. Вместо третьего столбца возьмем первый. Тогда получим отличный от нуля минор второго порядка 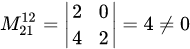 . Следовательно,
. Следовательно, 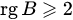 .
.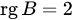 .
. . 1. Выбираем первую строку
. 1. Выбираем первую строку 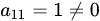 . Получили минор
. Получили минор  . Следовательно,
. Следовательно,  .
.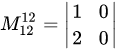 . Выбор второго столбца оказался неудачным, так как получили минор, равный нулю. Возьмем вместо второго третий столбец
. Выбор второго столбца оказался неудачным, так как получили минор, равный нулю. Возьмем вместо второго третий столбец  . Получим минор
. Получим минор 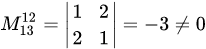 . Следовательно,
. Следовательно,  .
. . Имеется три окаймляющих минора
. Имеется три окаймляющих минора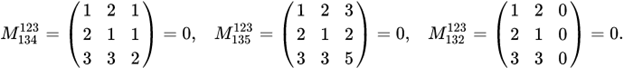
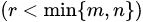 , то количество окаймляющих его миноров (r+l)-ro порядка равно
, то количество окаймляющих его миноров (r+l)-ro порядка равно 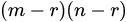 , а общее количество миноров (r+1)-го порядка гораздо больше.
, а общее количество миноров (r+1)-го порядка гораздо больше.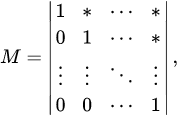
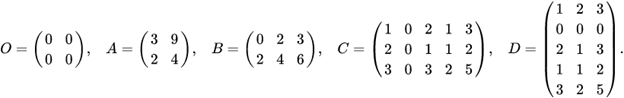
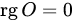 .
.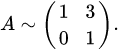
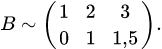
 , делаем равными нулю остальные элементы первого столбца: ко второй строке прибавляем первую, умноженную на (-2), к третьей строке — первую, умноженную на (-3). Получаем матрицу
, делаем равными нулю остальные элементы первого столбца: ко второй строке прибавляем первую, умноженную на (-2), к третьей строке — первую, умноженную на (-3). Получаем матрицу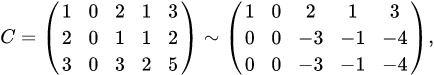
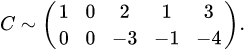
 .
.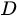 . 1. Приводим матрицу
. 1. Приводим матрицу 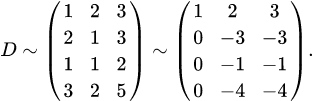
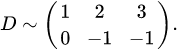
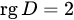 .
. , так как
, так как  (см. следствие 1 теоремы 3.4).
(см. следствие 1 теоремы 3.4).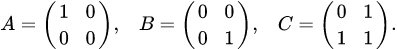
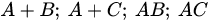 .
.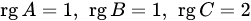 . Находим суммы и произведения данных матриц, а также их ранги:
. Находим суммы и произведения данных матриц, а также их ранги: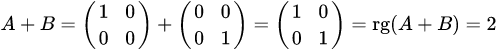 , то есть
, то есть 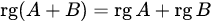 ;
;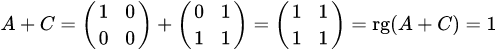 , то есть
, то есть 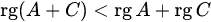 ;
;


