
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм решения обратной геодезической задачи способом БесселяСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Полагая, что известны геодезические координаты L 1, B 1 и L 2, B 2 двух точек на эллипсоиде, требуется найти кратчайшее расстояние S между этими точками и азимуты соответствующей геодезической линии: величину А12 в точке с координатами L 1, B 1 и величину А′21 во второй точке с координатами L 2, B 2. Задача решается в следующем порядке. Вычисляются значения приведенной широты для обеих точек и величина ΔL = L 2 – L 1 разности геодезических долгот. При практическом применении можно воспользоваться формулами вида (5.25) для получения sinu 1, cosu 1, sinu 2, cosu 2. Далее следует определить разность сферических долгот Δλ по разности геодезических долгот Δ L, связанных уравнением (5.24). После этого возможно решить задачу на сфере и пересчитать расстояния на эллипсоид. Однако, чтобы воспользоваться уравнением (5.24), следует предварительно получить значения σ, A 0 и σ1, которые, в свою очередь, зависят от искомых величин S и A 12. Поэтому уравнение (5.24) решается методом последовательных приближений. Укажем несколько способов решения. Первый способ: На первом шаге в предположении, что Δl = Δ L, находится нулевое приближение величины σ. Для этого используются формулы сферической тригонометрии вида (4.13):
Правые части уравнений обозначим соответственно p, q, n. Тогда:
На основании уравнения (5.26) вычисляется первое приближение sin A 0 и cos2 A 0:
На втором шаге определяется первое приближение разности долгот (5.24): Δλ = Δ L + sin A 0 ·K α·σ, причем коэффициент K α вычисляется по формуле (5.23). Вычисляются уточненные значения σ и A 0 с помощью формул вида (5.28)-(5.30), а значение σ1 из формулы (5.15):
Окончательно значение для Δλ определится по полной формуле (5.24):
Полученные значения приведенных широт u 1, u 2 и разности долгот Δ L определяют положение дуги большого круга (ортодромии), являющейся Бесселевым изображением геодезической линии. Азимуты этих линий равны, поэтому для определения угла А 21 можно использовать формулы сферической тригонометрии вида (5.13) и определять А 21 аналогично определению А 12:
Расстояние между заданными точками вычисляется с помощью формулы (5.21):
Второй способ: По формулам (5.25) вычисляются значения приведенных широт исходной и конечной точек. Разность сферических долгот определяется в виде Δl = Δ L + d l. Дальнейшие вычисления проводятся методом последовательных приближений. На первом шаге d l = 0. Далее по формулам (5.28)-(5.30) вычисляются A 12, cos2 A 0 и из уравнения (5.28) получается
Вычисляются коэффициенты K α и K β и поправка δλ. Для эллипсоида Красовского соответствующие формула имеют вид:
Вычисления проводятся итерационно, пока изменения dl не станут меньше 0,5×10-8 (радиан, т.е. около 0,01 угловой секунды – не более 30 см на поверхности). Далее вычисляются коэффициенты и значения дальности и углов:
Третий способ (Винсента): По формулам (5.41) вычисляются значения приведенных широт исходной и конечной точек. Разность сферических долгот определяется в виде Δl = Δ L + d l. Дальнейшие вычисления проводятся методом последовательных приближений. На первом шаге d l = 0. Из уравнения (5.28):
Далее вычисляются:
Вычисления проводятся итерационно, пока изменения dl не станут меньше 0,5×10-8. Далее вычисляются коэффициенты и значения дальности и углов:
Алгоритмы решения обратной геодезической задачи косвенным методом Существуют не итерационные способы вычисления геодезического расстояния, точность которых достаточна для многих задач. Приведем без вывода некоторые из них [7]. Метод Ламберта По формулам (5.41) вычисляются значения приведенных широт исходной и конечной точек. Разность сферических долгот определяется в виде Δl = Δ L. По формулам (5.28), (5.31) определяются s, sin s, cos s. Далее, учитывая величины большой полуоси земного эллипсоида a и его сжатия a, вычисляются вспомогательные параметры и искомая дальность S:
На расстояниях до 3000 км этот метод дает ошибку не более 5 м. Метод Андуайе Разность сферических долгот по-прежнему определяется в виде Δl = Δ L. Угловое расстояние s на сфере вычисляется по формулам (5.44), но при вычислении p, q, n используются значения геодезических, а не приведенных широт. Далее вычисляются вспомогательные параметры и искомая дальность S:
На расстояниях до 3000 км этот метод дает ошибку не более 30 м. Примечание: во всех случаях применения функции arctg() необходимо учитывать знаки числителя и знаменателя аргумента для правильного определения четверти и соответственно величины результирующего параметра. При программировании на языках высокого уровня для автоматического учёта знаков числителя и знаменателя необходимо использовать функцию atan2(x 1, x 2) с двумя аргументами, которая корректно вычисляет значение арктангенса от отношения x 1/ x 2, причем диапазон результата: от –π до π.
|
||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 612; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.14.104 (0.006 с.) |

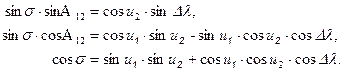 (5.28)
(5.28)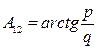 ;
; 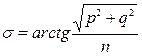 . (5.29)
. (5.29)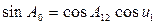 ;
; 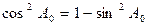 . (5.30)
. (5.30)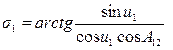 .
. .
.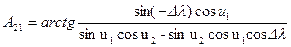 .
.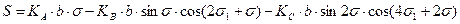 .
.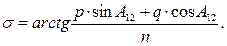
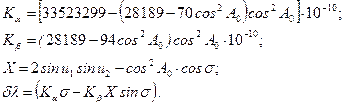
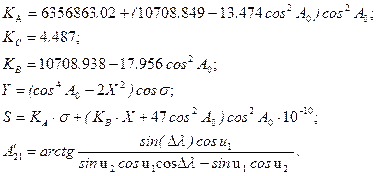
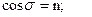
 ;
; 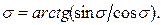 (5.31)
(5.31)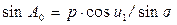 ;
; 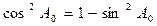 ;
;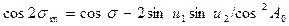 ;
;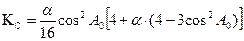 , где a - сжатие;
, где a - сжатие;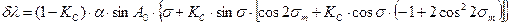 . (5.32)
. (5.32)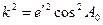 ;
; 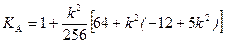 ;
; 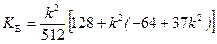 ;
;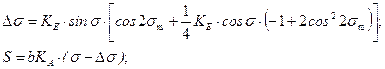 (5.33)
(5.33)
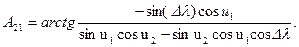
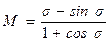 ;
; 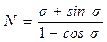 ;
;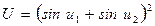 ; (5.34)
; (5.34)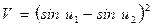 ;
;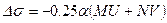 ;
;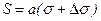 .
.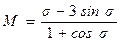 ;
;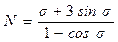 ;
;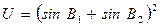 ;
;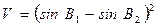 ; (5.35)
; (5.35)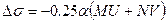 ;
;


