
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Практические алгоритмы решения прямой геодезической задачи способом БесселяСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Полагая, что на земном эллипсоиде построена геодезическая линия, азимут А 12 которой в точке А с координатами L 1 и B 1 известен, требуется найти геодезические координаты L 2 и B 2 другой точки В, принадлежащей этой же линии и отстоящей от точки А на заданное расстояние S (рис. 5.12). Алгоритм решения этой задачи с помощью Бесселева отображения предусматривает следующий порядок действий. Первый способ: 1. Вычисление приведенной широты исходной точки по заданной геодезической широте:
При практическом применении вычисляют
Эти формулы получаются из сравнения уравнений перевода геодезических координат в прямоугольные пространственные и соотношений X = a × cosu, Z = b × sinu. 2. Вычисление вспомогательных величин, используя формулы (5.31), (5.32) и известные значения азимута A 12 и широты u 1:
Если sinu1 = 0, то sin2s1 = 0 и cos2s1= 1. 5. Вычисление коэффициентов KA, K В, K С, Kα, Kβ по формулам (5.20) и (5.23). 4. Вычисление σ по S по формуле (5.22), применяя метод последовательных приближений. На первом шаге
На третьем шаге и четвертом шаге:
При этом используют соотношения:
5. Вычисление координат второй точки. (см. рис. 5.6). Из сферического треугольника А1В1Р1 определяется величина
Выразив из сферического треугольника А¢1А1В1 косинус дуги А¢1В1, далее из прямоугольного сферического треугольника А¢1В1В¢1 определяется косинус дуги А¢1В¢1, равной Dl:
Отсюда
Из сферического треугольника А1Р1B1 определяется
величина cos u 2 выражается из предыдущего уравнения для cos D l. Используя выражение (1.18), связывающее значения геодезической и приведенной широт точки, вычисляется широта:
6. Вычисление поправки dl по формуле:
и долготы в соответствии с (5.40): L 2 = L 1 + Dl - dl. Второй способ: Вычисления проводятся аналогично первому способу, несколько отличаясь следующем. Вычисляются коэффициенты разложения по формулам, имеющим следующий вид для эллипсоида Красовского:
Первое приближение сферического расстояния вычисляется по формуле:
Вычисляется второе приближение. При этом используются уравнения (5.26) и разложение, аналогичное (5.27):
Поправка к разности долгот вычисляется по формуле:
Широта точки вычисляется по формулам:
При необходимости, вычисляется азимут продолжения геодезической линии АВ в точке В:
Третий способ (Винсента): Особенности этого способа следующие. Параметры sin u 1, cos u 1, sin A 0, k2, cos2 A 0 определяются аналогично основному варианту, в частности:
Вычисляются вспомогательные величины:
Первое приближение углового расстояния на сфере определяется в виде:
Следующие выражения участвуют в итерационном процессе:
После двух итераций вычисляются координаты:
|
||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 687; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

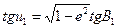 .
.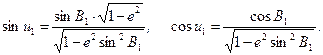 (5.25)
(5.25)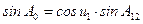 ;
; 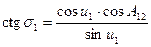 ;
;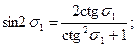
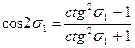 . (5.26)
. (5.26)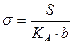 . На втором шаге:
. На втором шаге: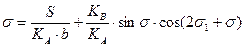 .
. .
.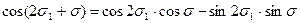 ;
;  . (5.27)
. (5.27)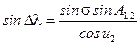 .
.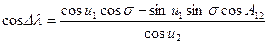 .
.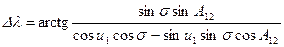 .
.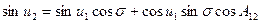 ,
,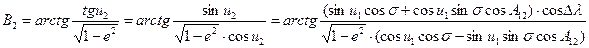 .
.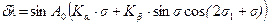 ,
,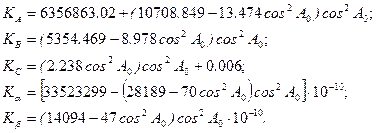
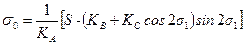 .
.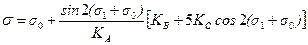 .
.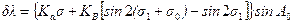 .
.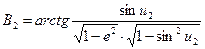 .
.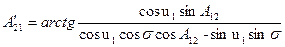 .
.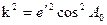 ;
; 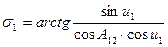 .
.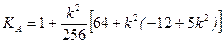 ,
, 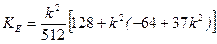 .
.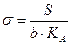 , где b – малая полуось земного эллипсоида.
, где b – малая полуось земного эллипсоида.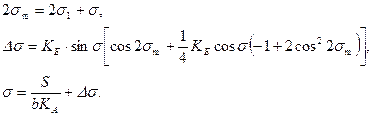
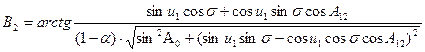 ;
;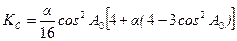 , где a - сжатие (a-b)/a,
, где a - сжатие (a-b)/a,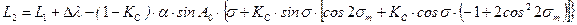 ;
;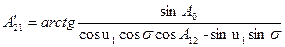 .
.


