
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление эллиптических интегралов при решении геодезических задач
Полученные выражения (5.13) и (5.14) могут быть использованы для численного определения с любой заданной точностью расстояний между двумя точками на эллипсоиде. Использование других способов отображения эллипсоида на сферу (например, по нормалям) приведет к появлению других выражений, основой которых, тем не менее, будут аналогичные эллиптические интегралы. Выбор метода численного интегрирования также будет приводить к появлению различных алгоритмов. Рассмотрим один из возможных способов вычисления неберущихся эллиптических интегралов при решении геодезических задач на эллипсоиде [8]. Оставляя прежние обозначения элементов полярного сферического треугольника А1В1Р1 (рис. 5.6), выполним вспомогательные построения, показанные на рис. 5.6: проведем из точки Р1 дугу большого круга перпендикулярно к продолжению стороны А1В1 до пересечения с ней в точке С1.
Рис. 5.6. К вычислению эллиптических интегралов В образовавшемся прямоугольном сферическом треугольнике А1С1Р1 обозначим длину катета С1Р1 через m, а длину катета А1С1 – через (π/2 – s1). При заданных значениях приведенной широты
а с учетом уравнения выражение для cos m запишется в виде:
По построению точка С1 – это точка вертекса ортодромии, проходящей через точки А1 и В1, следовательно, длина дуги D1C1 составляет четверть длины окружности, а угловая мера дуги D1C1 равна π/2. Это означает, что введенная выше величина s1 есть не что иное, как угловая мера дуги D1А1. У треугольника D1C1 P1 стороны D1C1 и D1 P1 равна π/2 следовательно, угловая мера дуги m равна углу A 0 (азимут геодезической линии в точке D1 пересечения ее с экватором). То же подтверждается при сопоставлении четвертого уравнения (5.15) и уравнения теоремы Клеро в виде (5.9), из которого следует sin m = sinA o, (5.16) Заменим m на A 0. Будем рассматривать точку В1 как текущую, имеющую широту
Подставив выражение для
или
Приняв во внимание формулы (1.0) вида
Или, после введения обозначения
получаем
Разложим подкоренное выражение в биноминальный ряд с целью последующего почленного интегрирования:
Не теряя общности, с целью получения практически пригодных формул в дальнейших выкладках ограничимся членами, имеющими порядок малости
получим
(5.19) Обозначив:
на основании (5.18) - (5.20) получим для интеграла (5.13):
Осуществляя почленное интегрирование, получим:
Обратная зависимость σ от S имеет вид:
Для вычисления интеграла (5.14) предварительно выразим d λ через d σ. Для этого выражение
Раскладывая в ряд подынтегральное выражение (5.14) и частично заменяя d λ, получаем:
Заменяя с помощью формулы
и, осуществляя почленное интегрирование, получим:
Обозначив
Получим окончательно
Формулы (5.22) и (5.24) используются при решении прямой геодезической задачи. При этом вычисление величины σ по известной величине S с помощью формулы (5.22) ведется методом последовательных приближений. Формулы (5.21) и (5.24) используются при решении обратной геодезической задачи. При этом вычисление Dl ведется методом последовательных приближений. Первое приближение Dl = DL, затем вычисляется σ и уточняется Dl и так далее. Вычисления продолжают до совпадения результатов вычислений двух последних приближений в пределах заданной точности.
|
||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 243; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.196.217 (0.008 с.) |

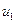 и азимута
и азимута  (равного a12) величины m и s1 легко отыщутся из решения прямоугольного треугольника А1С1Р1 относительно величин cos m, sin m, tgσ1:
(равного a12) величины m и s1 легко отыщутся из решения прямоугольного треугольника А1С1Р1 относительно величин cos m, sin m, tgσ1: ;
;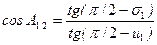
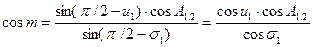 ;
;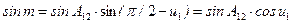 ; (5.15)
; (5.15)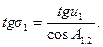
 . Из прямоугольного сферического треугольника В1С1Р1 имеем:
. Из прямоугольного сферического треугольника В1С1Р1 имеем: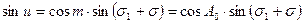 ,
,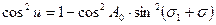 .
. в (5.29), получим
в (5.29), получим
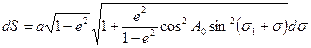 .
.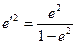 и
и 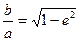 , перепишем подынтегральное выражения (5.13) как:
, перепишем подынтегральное выражения (5.13) как: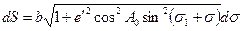 .
.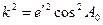 (5.17)
(5.17) . (5.18)
. (5.18)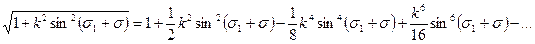 .
.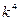 . Заменяя синусы четных степеней через косинусы кратных дуг на основании известных соотношений:
. Заменяя синусы четных степеней через косинусы кратных дуг на основании известных соотношений: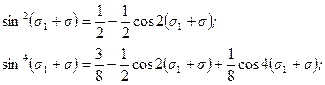
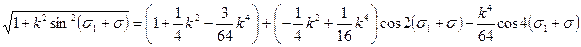 .
.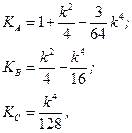 (5.20)
(5.20)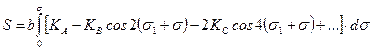 .
. 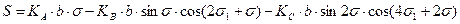 . (5.21)
. (5.21) . (5.22)
. (5.22)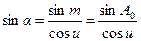 , полученное из рассмотрения прямоугольного сферического треугольника А1С1Р1, подставим во второе уравнение (5.10):
, полученное из рассмотрения прямоугольного сферического треугольника А1С1Р1, подставим во второе уравнение (5.10):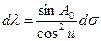 .
. 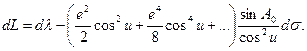
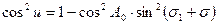 переменную
переменную 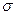 и используя выражения для
и используя выражения для 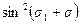 , перепишем (5.14) в виде:
, перепишем (5.14) в виде: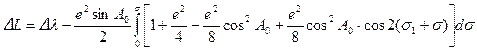
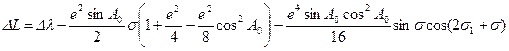 .
.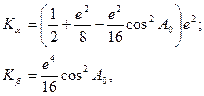 (5.23)
(5.23)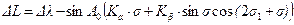 . (5.24)
. (5.24)


