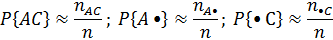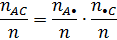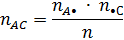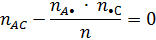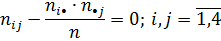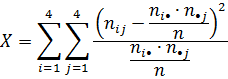Тестирование независимости соседних оснований нуклеотидной последовательности.

Основу решения данной задачи составляет таблица сопряженности оснований, которая имеет структуру – структуру матрицы размера 4×4

j i	A (j=1)	C (j=2)	G (j=3)	T (j=4)
A (i=1)	nАА	nАС	nАG	nАT	nA•
C (i=2)	nCA	nCC	nCG	nCT	nC•
G (i=3)	nGA	nGC	nGG	nGT	nG•
T (i=4)	nTA	nTC	nTG	nTT	nT•
	n•A	n•C	n•G	n•T

n_AA – количество динуклеотидов (пар нуклеотидов) типа «АА» в исследуемой последовательности

n_AС – количество динуклеотидов типа «АС» в исследуемой последовательности

n_A• – количество динуклеотидов в исследуемой последовательности, в первой позиции которых располагается основание А:

n_A• = n_AA + n_AC + n_AG + n_AT

n_•А – количество динуклеотидов в исследуемой последовательности, во второй позиции которых располагается основание А:

n_•А = n_AA + n_CA + n_GA + n_TA

Аналогичным образом заполняются все ячейки

Введем n – сумму всех элементов таблицы сопряженности.

Анализ независимости соседних оснований базируется на фундаментальном понятии теории вероятностей – понятии независимости случайных событий.

Случайные события {X}, {Y} – статистически независимыми, если вероятность совместного наступления этих событий равна произведению вероятностей наступления каждого из этих событий в отдельности.

P{XY} = P{X}∙P{Y}

Применим это фундаментальное понятие к анализу независимости двух конкретных оснований, образующих пару АС. В том случае, если между основаниями А и С, образующими нуклеотид, нет никакой связи, следуя приведенному выше фундаментальному определению, должно выполняться условие

P { AC }= P { A • }∙ P { • C },

где P{AC} – вероятность появления динуклеотида типа «АС» в исследуемой последовательности;

P{A•} – вероятность появления динуклеотида, первым основанием которого является основание А;

P{•С} – вероятность появления динуклеотида, вторым основанием которого является основание С;

В качестве оценок указанных вероятностей будем использовать их частоты.

Таким образом, признаком того, что соседние основания А и С не демонстрируют никакой связи, является выполнение следующего условия:

Выполнение этого условия позволяет утверждать, что никакой связи между основаниями А и С в исследуемой последовательности нет. Для того, чтобы утверждать, что в исследуемой нуклеотидной последовательности нет никакой связи между соседними основаниями, указанное условие должно выполняться для всех возможных парных комбинаций, т.е. для всех элементов таблицы сопряженности.

Иными словами, признаком того, что исследуемая нуклеотидная последовательность является абсолютно случайной комбинацией, является одновременное выполнение следующей совокупности шестнадцати условий:

Для проверки одновременного выполнения всей приведенной совокупности условий используется скалярная величина X, которая рассчитывается на основе следующего выражения:

Из вида приведенной величины следует, что её близкое к нулю значение указывает на то, что отсутствует какая-либо связь между соседними основаниями в исследуемой нуклеотидной последовательности. Напротив, чем больше эта величина, тем более выражена связь между соседними основаниями в исследуемой нуклеотидной последовательности.

Вопрос в том, какое значение этой величины считать достаточно большим, чтобы можно было уверенно и безошибочно говорить о наличии связи между соседними основаниями нуклеотидной последовательности.

Ответ на этот вопрос осложняет то обстоятельство, что появление того или иного основания в нуклеотидной последовательности является случайным событием. По этой причине определенная таким образом скалярная величина Х является случайной величиной. Для случайной величины невозможно указать фиксированный порог, который делит её значения на условно большие и условно малые, т.к. случайная величина может принимать любое значение с разной вероятностью.

Ответить на поставленный вопрос помогает доказанное свойство, которым обладает таким образом определенная случайная величина Х: если в исследуемой нуклеотидной последовательности отсутствует какая-либо связь между соседними основаниями, случайная величина Х имеет теоретическое χ² (хи-квадрат) распределение с числом степеней свободы равном 9.

χ²-распределение относится к классу теоретических распределений, связанных с нормальным распределением. Для него известны аналитические зависимости, описывающие закон распределения. Кроме того, в таблицах математической статистики приведены значения квантилей Х_α χ²-распределения для различных значений числа степеней свободы, соответствующие доверительным вероятностям α = 0.95, 0.99, 0.999

Квантилью Х_α называется уровень, который гарантированно с доверительной вероятностью α не будет превышен случайной величиной Х:

P{X ≤ X_α} = α.

Предположим, что Х_α – табличное значение квантили χ²-распределения, соответствующее доверительной вероятности 0.95. Пусть Х_Н – наблюдаемое значение случайной величины Х, рассчитанное с помощью таблицы сопряженности на основе приведенного выше выражения.

Тогда с вероятностью 0.95 при отсутствии какой-либо связи между соседними основаниями в нуклеотидной последовательности должно выполняться неравенство Х_Н ≤ X_α.

Выполнение этого неравенства позволяет утверждать, что в исследуемой последовательности отсутствует какая-либо связь между соседними основаниями. Причем достоверность этого заключения гарантирована вероятностью 0.95, т.е. вероятность того, что этот вывод ошибочен, не превышает 0.05.

Если имеет место неравенство X_H > X_α, с вероятностью 0.95 можно утверждать, что в исследуемой последовательности существует связь между какими-то соседними основаниями.

Если в результате решения этой задачи подтверждена связь между соседним основаниями, возникает следующая задача, связанная с оценкой глубины этой связи. Для решения этой задачи используется метод анализа марковских цепей.