
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Одноканальна система з необмеженою чергою
На практиці часто зустрічаються одноканальні СМО з необмеженою чергою (наприклад, телефон-автомат з однією будкою). Розглянемо завдання. Є одноканальна СМО з чергою, на яку не накладені ніякі обмеження (ні по довжині черги, ні за часом очікування). Потік заявок, що поступають в СМО, має інтенсивність, а потік обслуговуванні — інтенсивність Граф станів СМО представлений на мал. 3.
  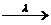 … …  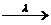 … …
Мал. 3 Це процес загибелі і розмноження, але з нескінченним числом станів, в якому інтенсивність потоку заявок рівна, а інтенсивність потоку обслуговуванні Перш ніж записати формули граничної вірогідності, необхідно бути упевненим в їх існуванні, адже у разі, коли час Для визначення граничної вірогідності станів скористаємося формулами для процесу загибелі і розмноження (тут ми допускаємо відому не строгість, оскільки раніше ці формули були одержані для випадку кінцевого числа станів системи). Одержимо:
Оскільки гранична вірогідність існує лише при р < 1, то геометричний ряд із знаменником р < 1, записаний в дужках у формулі (29), сходиться до суми, рівної. Тому з урахуванням співвідношень
Знайдемо граничні ймовірності інших станів
Гранична вірогідність р0, р1, р2, pk, утворюють убуваючу геометричну прогресію із знаменником р < 1, отже, вірогідність p0 найбільша. Це означає, що якщо СМО справляється з потоком заявок (при р < 1), то найбільш вірогідною буде відсутність заявок в системі. Середнє число заявок в системі Lсист визначимо по формулі математичного очікування, яка з урахуванням (31) прийме вигляд
(підсумовування від 1 до Можна показати, що формула (33) перетвориться (при р < 1) до вигляду
Знайдемо середнє число заявок в черзі Lоч. Очевидно, що
Lоч=Lсист - Lоб (35)
де Lоб — середнє число заявок, що знаходяться під обслуговуванням. Середнє число заявок під обслуговуванням визначимо по формулі математичного очікування числа заявок під обслуговуванням, що приймає значення 0 (якщо канал вільний) або 1 (якщо канал зайнятий):
тобто середнє число заявок під обслуговуванням рівне вірогідності того, що канал зайнятий:
По формулі (30)
Тоді отримаємо:
Доведено, що при будь-якому характері потоку заявок, при будь-якому розподілі часу обслуговування, при будь-якій дисципліні обслуговування середній час перебування заявки в системі (черги) рівна середньому числу заявок в системі (у черзі), що ділиться на інтенсивність потоку заявок, тобто
Формули (39) і (40) називаються формулами Літтла. Вони витікають з того, що в граничному, стаціонарному режимі середнє число заявок, що прибувають в систему, рівно середньому числу заявок, що покидають її: обидва потоки заявок мають одну і ту ж інтенсивність На підставі формул (39) і (40) з обліком (34) і (38) середній час перебування заявки в системі визначиться по формулі:
а середній час перебування заявки в черзі
|
|||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 53; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.183.150 (0.011 с.) |
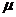 . Необхідно знайти граничну вірогідність станів і показники ефективності СМО. Система може знаходитися в одному із станів So S1, S2,., Sk, по числу заявок, що знаходяться в СМО: So — канал вільний;.S1 — канал зайнятий (обслуговує заявку), черги немає; S2— канал зайнятий, одна заявка стоїть в черзі; Sk — канал зайнятий, (до - 1) заявок стоять в черзі і т.д.
. Необхідно знайти граничну вірогідність станів і показники ефективності СМО. Система може знаходитися в одному із станів So S1, S2,., Sk, по числу заявок, що знаходяться в СМО: So — канал вільний;.S1 — канал зайнятий (обслуговує заявку), черги немає; S2— канал зайнятий, одна заявка стоїть в черзі; Sk — канал зайнятий, (до - 1) заявок стоять в черзі і т.д.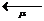

 …
… 
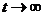 , черга може необмежено зростати. Доведено, що якщо р < 1, тобто середнє число заявок, що приходять, менше середнього числа обслужених заявок (у одиницю часу), то гранична вірогідність існує. Якщо р > 1, черга росте до безкінечності.
, черга може необмежено зростати. Доведено, що якщо р < 1, тобто середнє число заявок, що приходять, менше середнього числа обслужених заявок (у одиницю часу), то гранична вірогідність існує. Якщо р > 1, черга росте до безкінечності.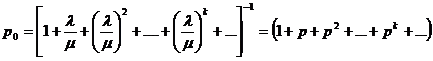 (29)
(29) (31)
(31) (32)
(32)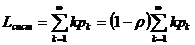 (33)
(33) , оскільки нульовий член p0 = 0).
, оскільки нульовий член p0 = 0).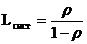 (34)
(34)
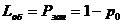 (36)
(36) (37)
(37) (38)
(38) (39)
(39) (40)
(40)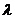 .
.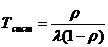 (41)
(41)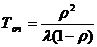 (42)
(42)


