
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття марківського випадкового процесу
Процес роботи СМО є випадковим процесом. Під випадковим (імовірнісним або стохастичним) процесом розуміється процес зміни в часі стану якої-небудь системи відповідно до імовірнісних закономірностей. Процес називається процесом з дискретними станами, якщо його можливі стани S1, S2, S3... можна наперед перерахувати, а перехід системи із стану в стан відбувається миттєво (стрибком). Процес називається процесом з безперервним часом, якщо моменти можливих переходів системи із стану в стан не фіксовані наперед, а випадкові. Процес роботи СМО є випадковим процесом з дискретними станами і безперервним часом. Це означає, що стан СМО міняється стрибком у випадкові моменти появи якихось подій (наприклад, приходу нової заявки, закінчення обслуговування і т.п.). Математичний аналіз роботи СМО істотно спрощується, якщо процес цієї роботи - марківський. Випадковий процес називається марківським або випадковим процесом без наслідку, якщо для будь-якого моменту часу t0 імовірнісні характеристики процесу в майбутньому залежать тільки від його стану в даний момент t0 і не залежать від того, коли і як система прийшла в цей стан. Приклад марківського процесу: система S - лічильник у таксі. Стан системи у момент t характеризується числом кілометрів (десятих доль кілометрів), пройдених автомобілем до даного моменту. Хай у момент t лічильник показує S0. Вірогідність того, що у момент t > t0 лічильник покаже те або інше число кілометрів (точніше, відповідне число рублів) S1, залежить від S0, але не залежить від того, в які моменти часу змінювалися свідчення лічильника до моменту t0. Багато процесів можна приблизно вважати марківськими. Наприклад, процес гри в шахи; система S - група шахових фігур. Стан системи характеризується числом фігур супротивника, що збереглися на дошці в момент t0. Вірогідність того, що у момент t > t0 матеріальна перевага буде на стороні одного з супротивників, залежить в першу чергу від того, в якому стані знаходиться система в даний момент t0 а не того, коли і в якій послідовності зникли фігури з дошки до моменту t0. У ряді випадків передісторією даних процесів можна просто нехтувати і застосовувати для їх вивчення марківські моделі. При аналізі випадкових процесів з дискретними станами зручно користуватися геометричною схемою - так званим графом станів. Звичайно стани системи зображаються прямокутниками, а можливі переходи із стану в стан - стрілками (орієнтованими дугами), що сполучають стани.
Рівняння для аналізу СМО Основні рівняння СМО
Закон Бернуллі. В основі аналізу СМО лежить біноміальний закон Бернуллі, який дозволяє розраховувати ймовірність появи події "А" точно К разів при п незалежних іспитах (тільки для дискретних випадкових взаємно несумісних незалежних подій):
де п - кількість незалежних іспитів; Рn(К) - ймовірність появи подій "А" точно К разів при п незалежних іспитах; р - ймовірність появи однієї події "А"; q =1- р — ймовірність протилежної події (не появи події "А"); К — кількість появи події "А" при и спостереженнях; У принципі закон Бернуллі (і закони Лапласа та Пуассона, що з нього випливають) може використовуватись для визначення конструкції СМО - кількості каналів обслуговування та середнього строку обслуговування однієї вимоги. Якщо прийняти К = 0, 1,2..., n, то отримаємо повну групу взаємно несумісних подій, для якої сума відповідних ймовірностей
Формула Стірлінга. Формула Бернуллі дуже складна для обчислення, тому використовується формула Стерлінга
у якій точність розрахунків збільшується при Формула Лапласа. Подальші перетворення формули Бернуллі дозволяють отримати формулу Лапласа
де Із формули Лапласа випливає, що при
і ймовірність найімовірнішого числа подій Ко дорівнює
З точністю до Формула Пуассона. При великій кількості незалежних іспитів (n» 1), малій ймовірності одного з іспитів
де Ймовірність появи події "А" не більше за т разів
Ймовірність того, що подія "А" при п іспитах зовсім не з'являється Формула Пуассона використовується для розрахунку різних подій. При цьому вважається, що
де Ймовірність появи одного телефонного дзвінка, однієї відмови пристрою і т.п.
Постійна величина формули Пуассона
Диференційні рівняння СМО
Стан · в одноканальній СМО з очікуванням - довжиною черги i; · у багатоканальній СМО з відмовами - кількістю зайнятих каналів і(у цій СМО черги немає: якщо всі канали зайняті то вимога не обслуговується і зникає); · у багатоканальній СМО з очікуванням - числом зайнятих каналів плюс довжиною черги. Розглянемо досить велику кількість N таких ідентичних СМО. Позначимо через Рі ймовірність того, що СМО знаходиться на час t у стані Si, а через У СМО вважається, що потік вимог підкоряється пуассонівському закону. Тому за малий термін Тоді згідно з законом Пуассона (ймовірність появи точно k подій із п можливих за проміжок часу t) при умовах k= 1, t =
Таким чином, ймовірність надходження точно однієї події дорівнює
де Одночасно вважається, що обслуговування теж підкоряється експоненціальному закону і тому ймовірність завершення обслуговування точно однієї події
4. СМО з відмовами
Як показники ефективності СМО| з|із| відмовами розглядатимемо|розглядуватимемо|: А — абсолютну пропускну спроможність СМО|, тобто середнє число заявок, що обслуговуються в одиницю часу; Q — відносну пропускну спроможність, тобто середню частку|долю| заявок, що прийшли, обслуговуються системою; Ротк— вірогідність|ймовірність| відмови, тобто того, що заявка покине СМО| не обслуженою; k— середнє число зайнятих каналів (для багатоканальної системи).
|
||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 134; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.202.167 (0.017 с.) |
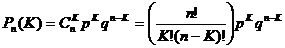 , (1)
, (1)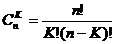 ; (2)
; (2)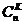 - сполучення по К елементів із п спостережень.
- сполучення по К елементів із п спостережень.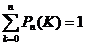 . (3)
. (3)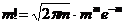 (4)
(4)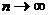 .
.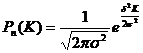 , (5)
, (5)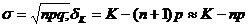
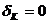 або при К= Ко (тут Ко - найімовірніша кількість подій "А") отримуємо
або при К= Ко (тут Ко - найімовірніша кількість подій "А") отримуємо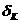 =К0 -пр = 0; К0 =пр (6)
=К0 -пр = 0; К0 =пр (6)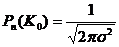 (7)
(7)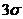 (тобто з ймовірністю 0,997) можна вважати, що всі події відбудуться, якщо виконується умова К — Ко
(тобто з ймовірністю 0,997) можна вважати, що всі події відбудуться, якщо виконується умова К — Ко 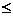
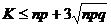
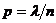 (тут
(тут 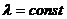 ) формула Лапласа дає помилки, і тому використовують асимтотичну формулу Пуассона
) формула Лапласа дає помилки, і тому використовують асимтотичну формулу Пуассона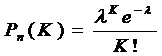 , (8)
, (8)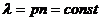 .
.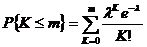 (9)
(9)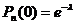 .
.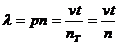 , (10)
, (10)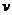 — середня кількість телефонних дзвінків за одиницю часу;
— середня кількість телефонних дзвінків за одиницю часу; 
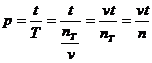 (11)
(11)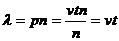 і формула Пуассона набуває вигляду
і формула Пуассона набуває вигляду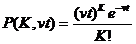 . (12)
. (12)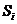 СМО визначається:
СМО визначається: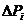 - зміну ймовірності Рі за малий проміжок часу
- зміну ймовірності Рі за малий проміжок часу 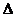 t.
t.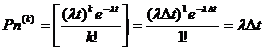 (13)
(13)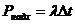 , (14)
, (14)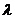 - інтенсивність надходження вимог.
- інтенсивність надходження вимог.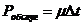 , де
, де 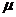 - інтенсивність обслуговування
- інтенсивність обслуговування


