
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Одноканальна система з відмовами.Содержание книги Поиск на нашем сайте
Запоріжжя 20 12
ЗМІСТ Вступ 1. Теоретичні аспекти теорії масового обслуговуванн. 1.1 Математичне моделювання систем масового обслуговування. 2. Поняття марківського випадкового процесу. 3. Рівняння для аналізу СМО. Основні рівняння СМО. Диференційні рівняння СМО. СМО з відмовами. Одноканальна система з відмовами. Багатоканальна система з відмовами. СМО з очікуванням (чергою). 5.1 Одноканальна система з необмеженою чергою. Багатоканальна СМО з необмеженою чергою. СМО з обмеженою чергою. Висновки Список використаної літератури.
Основи знань про черги, іноді звані теорією черг або теорією масового обслуговування, складають важливу частину теорії управління виробництвом. Черги — звичайне явище. Вони можуть носити форму очікування ремонту автомобіля в центрі автосервісу або очікування студентами консультації у професора. Моделі черг (як і лінійне програмування, моделі управління запасами, методи мережевого аналізу проектів) використовуються і у сфері управління матеріальним виробництвом, і у сфері обслуговування. Аналіз черг в термінах довжини черги, середнього часу очікування, середнього часу обслуговування і інших чинників допомагає нам краще зрозуміти принципи організації системи обслуговування. Метою даної роботи є аналіз систем масового обслуговування, їх особливостей, а також вивчення методів розв’язку систем масового обслуговування і практичне їх застосування. Задача даної роботи – провести детальний аналіз систем масового обслуговування, а також практично застосувати методи їх розв’язку. Структура роботи. Відповідно до мети і задачі, дана робота складається із вступу, теоретичної частини, практичної частини, висновків і списку літератури. В теоретичній частині розглядається загальна теорія курсової роботи, в практичній частині – приклад розв’язку статистичної задачі з використанням методів розв’язку, приведених в теоретичній частині. Рівняння для аналізу СМО Основні рівняння СМО
Закон Бернуллі. В основі аналізу СМО лежить біноміальний закон Бернуллі, який дозволяє розраховувати ймовірність появи події "А" точно К разів при п незалежних іспитах (тільки для дискретних випадкових взаємно несумісних незалежних подій):
де п - кількість незалежних іспитів; Рn(К) - ймовірність появи подій "А" точно К разів при п незалежних іспитах; р - ймовірність появи однієї події "А"; q =1- р — ймовірність протилежної події (не появи події "А"); К — кількість появи події "А" при и спостереженнях; У принципі закон Бернуллі (і закони Лапласа та Пуассона, що з нього випливають) може використовуватись для визначення конструкції СМО - кількості каналів обслуговування та середнього строку обслуговування однієї вимоги. Якщо прийняти К = 0, 1,2..., n, то отримаємо повну групу взаємно несумісних подій, для якої сума відповідних ймовірностей
Формула Стірлінга. Формула Бернуллі дуже складна для обчислення, тому використовується формула Стерлінга
у якій точність розрахунків збільшується при Формула Лапласа. Подальші перетворення формули Бернуллі дозволяють отримати формулу Лапласа
де Із формули Лапласа випливає, що при
і ймовірність найімовірнішого числа подій Ко дорівнює
З точністю до Формула Пуассона. При великій кількості незалежних іспитів (n» 1), малій ймовірності одного з іспитів
де Ймовірність появи події "А" не більше за т разів
Ймовірність того, що подія "А" при п іспитах зовсім не з'являється Формула Пуассона використовується для розрахунку різних подій. При цьому вважається, що
де
Ймовірність появи одного телефонного дзвінка, однієї відмови пристрою і т.п.
Постійна величина формули Пуассона
Диференційні рівняння СМО
Стан · в одноканальній СМО з очікуванням - довжиною черги i; · у багатоканальній СМО з відмовами - кількістю зайнятих каналів і(у цій СМО черги немає: якщо всі канали зайняті то вимога не обслуговується і зникає); · у багатоканальній СМО з очікуванням - числом зайнятих каналів плюс довжиною черги. Розглянемо досить велику кількість N таких ідентичних СМО. Позначимо через Рі ймовірність того, що СМО знаходиться на час t у стані Si, а через У СМО вважається, що потік вимог підкоряється пуассонівському закону. Тому за малий термін Тоді згідно з законом Пуассона (ймовірність появи точно k подій із п можливих за проміжок часу t) при умовах k= 1, t =
Таким чином, ймовірність надходження точно однієї події дорівнює
де Одночасно вважається, що обслуговування теж підкоряється експоненціальному закону і тому ймовірність завершення обслуговування точно однієї події
4. СМО з відмовами
Як показники ефективності СМО| з|із| відмовами розглядатимемо|розглядуватимемо|: А — абсолютну пропускну спроможність СМО|, тобто середнє число заявок, що обслуговуються в одиницю часу; Q — відносну пропускну спроможність, тобто середню частку|долю| заявок, що прийшли, обслуговуються системою; Ротк— вірогідність|ймовірність| відмови, тобто того, що заявка покине СМО| не обслуженою; k— середнє число зайнятих каналів (для багатоканальної системи).
СМО з очікуванням (чергою)
Як показники ефективності СМО з очікуванням, окрім вже відомих показників — абсолютної А і відносної Q пропускної спроможності, вірогідності відмови Ротк,, середнього числа зайнятих каналів СМО з обмеженою чергою
СМО з обмеженою чергою відрізняються від розглянутих вище завдань лише тим, що число заявок в черзі обмежене (не може перевершувати деякого заданого т). Якщо нова заявка поступає в мить, коли всі місця в черзі зайняті, вона покидає СМО не обслуженої, тобто дістає відмову.
Очевидно: для обчислення граничної вірогідності станів і показників ефективності таких СМО може бути використаний той же підхід, що і вище, з тією різницею, що підсумовувати треба не нескінченну професію (як, наприклад, ми робили при виведенні формули (30)), а кінцеву. Середній час перебування заявки в черзі і в системі, як і раніше, визначаємо по формулах Літтла.
Висновки
У системах масового обслуговування (СМО) розглядаються черги і вирішуються питання по обслуговуванню ряду (потоку) вимог від людей, приладів, подій. Предметом теорії масового обслуговування є побудова математичних моделей, що пов'язують задані умови роботи СМО (число каналів, їх продуктивність, характер потоку заявок і т.п.) з показниками ефективності СМО, що описують її здатність справлятися з потоком заявок. Приклади СМО: черга у магазині (касир розглядається як прилад, що обслуговує чергу); телефонна станція (розглядається як прилад, що обслуговує потік замовлень на телефонні розмови); оператори ЕОМ (вони розглядаються сумісно з ЕОМ як прилад, що обслуговує потік інформації від приладів, підприємств та інших операторів). Вимоги на виконання робіт поступають у випадкові моменти часу, обслуговуючі пристрої задовольняють вимоги (обробляють їх) за випадковий термін. Кількість вимог є статистично оціненою величиною. Таким чином, СМО має дві головні ознаки: обслуговуючий пристрій і чергу. Процес роботи СМО є випадковим процесом. Математичний аналіз роботи СМО істотно спрощується, якщо процес цієї роботи - марківський. Випадковий процес називається марківським або випадковим процесом без наслідку, якщо для будь-якого моменту часу t0 імовірнісні характеристики процесу в майбутньому залежать тільки від його стану в даний момент t0 і не залежать від того, коли і як система прийшла в цей стан. СМО розрізняються: 1. За конструкцією обслуговуючого пристрою: одноканальна, багатоканальна. 2. За дисципліною черги. Найбільше розповсюджено правило: перший прийшов - перший обслуговуєшся. Але у СМО розглядаються й інші варіанти обслуговування, наприклад: - вимоги за пріоритетом; - відсутність черги (якщо для обслуговування черги немає вільного каналу або якщо СМО зайнята, то вимога не задовольняється і зникає). При аналізі СМО намагаються одержати такі характеристики: - середню довжину черги; - середній термін обслуговування; - середній час, за який обслуговуючий пристрій не працює. При дослідженні СМО звичайно вважають, що вхідний потік вимог підпорядковується закону Пуассона, за яким розглядають відносно рідкі події. За законом Пуассона ймовірність появи точно К подій із n за проміжок часу t.
Список використаної літератури: 1. Исследование операций в экономике: Учеб. пособие для вузов/ Н.Ш. 2. Кремер, Б.А. Петько, И.М. Тришин, М.Н. Фридман; Под ред. проф. Н.Ш. Кремера. - М.: Банки й биржи, ЮНИТИ, 1997. 3. Ю.П.Зайченко. Дослідження операцій. – Київ:ЗАТ “Віпол”, 2000. – 688 с. 4. С.І.Наконечний,С.С.Савіна Математичне програмування: Навч.посіб.– К.:КНЕУ,2003. 5. Кутковецький В.Я.. Дослідження операцій: Навчальний посібник.– Київ: Вид-во ТОВ “Видавничий дім “Професіонал”,2004. 6. 6. Катренко А.В. Дослідження операцій. Підручник. – Львів: «Магнолія» Плюс», 2004.
Запоріжжя 20 12
ЗМІСТ Вступ 1. Теоретичні аспекти теорії масового обслуговуванн. 1.1 Математичне моделювання систем масового обслуговування. 2. Поняття марківського випадкового процесу. 3. Рівняння для аналізу СМО. Основні рівняння СМО. Диференційні рівняння СМО. СМО з відмовами. Одноканальна система з відмовами.
|
||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 155; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.227.73 (0.008 с.) |

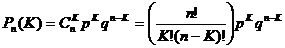 , (1)
, (1)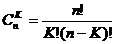 ; (2)
; (2)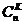 - сполучення по К елементів із п спостережень.
- сполучення по К елементів із п спостережень.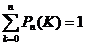 . (3)
. (3)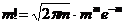 (4)
(4)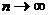 .
.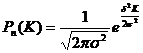 , (5)
, (5)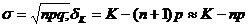
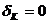 або при К= Ко (тут Ко - найімовірніша кількість подій "А") отримуємо
або при К= Ко (тут Ко - найімовірніша кількість подій "А") отримуємо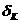 =К0 -пр = 0; К0 =пр (6)
=К0 -пр = 0; К0 =пр (6)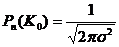 (7)
(7)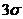 (тобто з ймовірністю 0,997) можна вважати, що всі події відбудуться, якщо виконується умова К — Ко
(тобто з ймовірністю 0,997) можна вважати, що всі події відбудуться, якщо виконується умова К — Ко 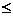
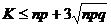
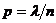 (тут
(тут 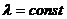 ) формула Лапласа дає помилки, і тому використовують асимтотичну формулу Пуассона
) формула Лапласа дає помилки, і тому використовують асимтотичну формулу Пуассона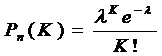 , (8)
, (8)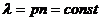 .
.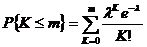 (9)
(9)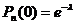 .
.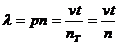 , (10)
, (10)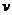 — середня кількість телефонних дзвінків за одиницю часу;
— середня кількість телефонних дзвінків за одиницю часу; 
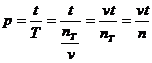 (11)
(11)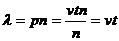 і формула Пуассона набуває вигляду
і формула Пуассона набуває вигляду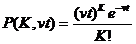 . (12)
. (12)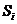 СМО визначається:
СМО визначається: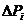 - зміну ймовірності Рі за малий проміжок часу
- зміну ймовірності Рі за малий проміжок часу 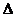 t.
t.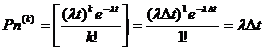 (13)
(13)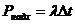 , (14)
, (14)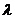 - інтенсивність надходження вимог.
- інтенсивність надходження вимог.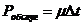 , де
, де 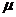 - інтенсивність обслуговування
- інтенсивність обслуговування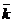 (для багатоканальної системи) розглядатимемо також наступні: Lсист— середнє число заявок в системі; Tсист — середній час перебування заявки в системі; Loч — середнє число заявок в черзі { довжина черги); Точ — середній час перебування заявки в черзі; Рзан — вірогідність того, що канал зайнятий (ступінь завантаження каналу).
(для багатоканальної системи) розглядатимемо також наступні: Lсист— середнє число заявок в системі; Tсист — середній час перебування заявки в системі; Loч — середнє число заявок в черзі { довжина черги); Точ — середній час перебування заявки в черзі; Рзан — вірогідність того, що канал зайнятий (ступінь завантаження каналу).


