
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модуль 1. Задача линейного программирования и ее геометрическое истолкованиеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Содержание Тема 1. Составление математических моделей экономических задач. Тема 2. Графический метод нахождения оптимального решения ЗЛП. Контрольная работа «Графический метод решения ЗЛП»
Тема 1. составление Математических моделей экономических задач
Примеры решения типовых задач Пример 1. Задача об использовании ресурсов Предприятие располагает двумя видами сырья S 1 и S 2 в количествах 10 и 15 условных единиц и изготавливает из него изделия трех видов П 1, П 2 и П 3. Известен расход каждого вида сырья на единицу продукции, что задается матрицей расхода сырья Составить экономико-математическую модель задачи. Для наглядности данные задачи занесем в таблицу. Таблица – Исходные данные задачи об использовании сырья
Построим экономико-математическую модель. Запишем искомый план производства в виде
а целевая функция (прибыли) Математическая модель задачи имеет стандартную форму. Пример 2. Задача составления рациона (о диете, о смесях), или технологическая задача. Стоимость 1 кг корма вида I – 4 рубля, а вида II – 6 рублей. Используя данные таблицы, необходимо составить такой рацион питания, чтобы стоимость его была минимальной и содержание каждого вида питательных веществ было не менее установленного предела. Таблица - Данные задачи о рационе питания
Модель задачи будет иметь вид:
Пример 3. Технологическая задача (о раскрое материала). Найти план раскроя, обеспечивающий максимальное число комплектов. Для изготовления брусьев длиной 1,2 м, 3 м и 5 м в соотношении 2:1:3 на распил поступает 195 бревен длиной 6 м. Определить план распила, обеспечивающий максимальное число комплектов. Составим модель задачи. Определим сначала все возможные способы распила бревен, указав соответствующее число получающихся при этом брусьев и остаток. Таблица - Способы распила бревен
Через хi обозначим число бревен распиливаемых i-м способом, Тогда экономико-математическая модель задачи будет иметь вид:
Задачи для самостоятельного решения Задача 1. Составить математическую модель задачи. Для изготовления изделий А и В используется 3 вида сырья. В таблице приведены нормы расхода сырья всех видов на изготовление единицы каждого вида изделий, запасы сырья и прибыль от реализации единицы продукции А и В. Таблица 2
Задача 2. Составить математическую модель задачи. На мебельной фабрике из стандартных листов фанеры необходимо вырезать заготовки трех видов в количестве не менее 24, 30 и 30 штук. Каждый лист фанеры может быть разрезан на заготовки двумя способами. В таблице приведено количество получаемых заготовок и величины отходов, которые получаются при раскрое одного листа фанеры при каждом способе. Сколько листов фанеры по каждому способу следует раскроить, чтобы получить минимальные отходы от раскроя? Таблица 3
Указание. Задача 3. Составить математическую модель задачи. На станках Р1 и Р2 производится два вида продукции А и В. Для изготовления 1 ед. продукции А станок Р1 используется 2 часа, а станок Р2 - 3 час. Для 1 ед. продукции В это время равно соответственно 1 час и 2 часа. Продукции А должно быть произведено не более 4 ед. В течение суток станок Р1 может работать не более 12 часов, а станок Р2 - не более 5 часов. От реализации 1 ед. А прибыль составляет 2 ден. ед., а от 1 ед. В - 1 ден. ед. Какое количество продукции вида А и В нужно произвести, чтобы чистая прибыль была максимальной? Указание.
Задача 4. Составить математическую модель задачи. Доски длиной 4,5 м, имеющиеся в достаточном количестве, следует распилить на заготовки длиной 1,7 м и длиной 1,4 м, причем заготовок первого вида должно быть получено не менее 86 штук и заготовок второго вида - не менее 90 штук. Каждая доска может быть распилена на указанные заготовки несколькими способами. 1) Требуется найти число досок, распиливаемых каждым способом, с тем, чтобы наименьшее количество заготовок было получено: 1) из наименьшего числа досок; 2) при минимальных отходах. Указание. Для составления математической модели задачи нужно сначала определить всевозможные способы распила на заготовки нужной длины и подсчитать остатки доски от раскроя по каждому способу раскроя. Задача 5. Составить математическую модель задачи. Фирма производит и продает два типа товаров. Фирма получает прибыль в размере 12 тыс.р. от производства и продажи каждой единицы товара 1 и в размере 4 тыс.р. от производства и продажи каждой единицы товара 2. Фирма состоит из трех подразделений. Затраты труда (чел-дни) на производство этих товаров в каждом из подразделений указаны в таблице.
Руководство рассчитало, что в следующем месяце фирма будет располагать следующими возможностями обеспечения производства трудозатратами: 1800 чел-дней в подразделении 1, 1600 — в подразделении 2 и 2000 — в подразделении 3. Задача 6. Составить математическую модель задачи Телевизионная компания производит два вида телевизоров — "Астро" и "Космо". Имеются две производственные линии, каждая для своего типа телевизоров. Мощность линии по производству "Астро" составляет 70 телевизоров в день, а "Космо" — 50 единиц в день. Цех А производит телевизионные трубки. В этом цехе на производство одной трубки к телевизору "Астро" требуется потратить 1,8 чел-ч, а на производство трубки к "Космо" — 1,2 чел-ч. В настоящее время в цехе А на производство трубок к обеим маркам телевизоров может быть затрачено не более 120 чел-ч в день. В цехе Б производятся шасси. В этом цехе на производство одной единицы шасси как к телевизору "Астро", так и к "Космо" требуется затратить 1 чел-ч. В цехе Б на производство шасси к обеим маркам телевизоров может быть затрачено не более 90 чел-ч. Продажа каждого телевизора марки "Астро" обеспечивает получение прибыли в размере 150 тыс.р., а марки "Космо" — 200 тыс.р. Задача 7. Составить математическую модель задачи. В задаче выбора вариантов примем, что для получения результата в виде максимально возможной прибыли необходимо два вида ресурсов: материальные и трудовые Возможны четыре варианта расхода ресурсов и получения прибыли (табл.).
Показатели |
Варианты | Наличие | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 2 | 3 | 4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Прибыль, д.е./ед. Материальные ресурсы Трудовые ресурсы | 65 200 10 | 80 180 15 | 90 240 22 | 210 250 28 | – 800 50 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Требуется выбрать, какие варианты принять для реализации при условии, чтобы общее число принятых вариантов не превышало трех.
|
| Поделиться: |

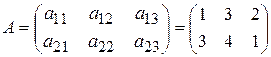 . Известна прибыль от реализации единицы продукции, которая задается вектором
. Известна прибыль от реализации единицы продукции, которая задается вектором 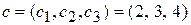 . Найти такой план производства продукции, от реализации которого предприятие получит максимальную прибыль.
. Найти такой план производства продукции, от реализации которого предприятие получит максимальную прибыль.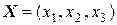 , где
, где 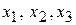 - количество единиц продукции П 1, П 2, П 3 соответственно. Система ограничений по расходу сырья примет вид
- количество единиц продукции П 1, П 2, П 3 соответственно. Система ограничений по расходу сырья примет вид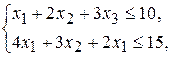
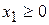 ,
, 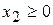 ,
, 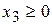 ,
,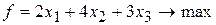 .
.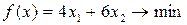
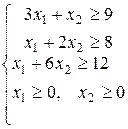
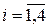 , а через х – число комплектов брусьев.
, а через х – число комплектов брусьев.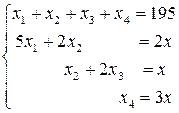
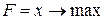
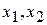 - количество листов фанеры, раскраиваемых по 1-му и 2-му способам. Ограничения по количеству заготовок - неравенства вида
- количество листов фанеры, раскраиваемых по 1-му и 2-му способам. Ограничения по количеству заготовок - неравенства вида 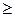 . Целевая функция
. Целевая функция 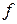 - общие отходы от раскроя.
- общие отходы от раскроя.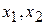 - количество продукции вида А (вида В). Целевая функция - это доход от реализации продукции.
- количество продукции вида А (вида В). Целевая функция - это доход от реализации продукции.


