Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Контрольная работа №1 «Графический метод решения ЗЛП»Содержание книги Поиск на нашем сайте
Примерные задачи в контрольной работе Задача. Решить графическим методом задачу линейного программирования
Модуль 2. Симплексный метод решения ЗЛП. Двойственность в линейном программировании Содержание Тема 3. Симплексный метод решения задач линейного программирования. Тема 4. Решение экономических ЗЛП симплексным методом. Контрольная работа «Симплексный метод решения ЗЛП» Тема 5. Двойственные задачи Тема 6. Решение экономических ДЗ симплексным методом. Самостоятельная работа «Экономический смысл теории двойственности»
Тема 3. Симплексный метод нахождения оптимального решения Примеры решения типовых задач Пример. Найти исходное опорное решение ЗЛП.
Запишем задачу в канонической форме, вводя в левую часть первого неравенства системы ограничений дополнительную переменную
Заполним симплексную таблицу 10 (
Таблица 10
Чтобы получить еще одну базисную переменную, обратимся к столбцам небазисных переменных Составим для положительных элементов разрешающего столбца симплексные отношения Таблица 11
В таблице 8 имеется теперь три базисные переменные
Приравняем к нулю свободные переменные Пример 4. Проверить, будет ли решение Решение Заполним
Таблица 12
Вычислим оценки свободных переменных, значение целевой функции
Таблица 13
Проверим, будет ли решение Теперь проверим, можно ли решение Пример 5. Выполнить переход от решения Решение Рассмотрим симплексную таблицу 13, из которой следует решение 1. Выберем наибольшую по абсолютной величине отрицательную оценку 2. Для положительных элементов разрешающего столбца
3. Проведем в таблице итерацию симплексных преобразований с выбранным разрешающим элементом: - разделим каждый элемент разрешающей строки на разрешающий элемент a 33 = 2; - в разрешающем столбце все элементы, кроме разрешающего элемента, заменим нулями; - все остальные элементы таблицы, включая Таблица 14
4. Запишем новое опорное решение Значение целевой функции находится в правом нижнем углу симплексной таблицы: 5. Новое опорное решение
Решение 6. Отрицательная оценка Таблица 15
Опорное решение Ответ: Задачи для самостоятельного решения
Задача 10. Найти исходное опорное решение в задачах линейного программирования. 1. Ответ: Х0=(1, 2, 0, 0, 4), f (X 0)=3. Ответ: Х0=(0, 0, 7, 3, 4), f (Х0)=10. 3. Ответ: Х0=(0, 2, 0, 3, 1), f (Х0)=1. Ответ: Х0=(0.5, 0.5, 0, 1), f (Х0 )= 2,5. Задача 11. Найти оптимальное решение задач линейного программирования. 1. Ответ: 1. Задача 12. Найти симплексным методом оптимальное решение задачи линейного программирования 1. Задача 13. Найти симплексным методом оптимальное решение экономической задачи. Предприятие производит два вида изделий А и В, используя сырье четырех видов. Расход сырья каждого вида на изготовление единицы продукции, запасы сырья и цены готовой продукции приведены в таблице. Таблица 16 Сырье |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 161; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.131.90.193 (0.011 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

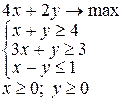

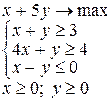
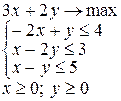
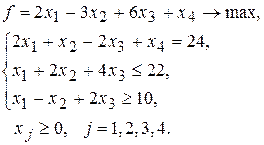
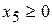 со знаком «+», а в левую часть второго неравенства дополнительную переменную
со знаком «+», а в левую часть второго неравенства дополнительную переменную 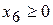 со знаком «минус».
со знаком «минус».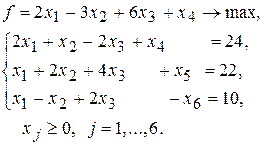
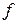 -строку не заполняем, пока система не будет приведена к единичному базису). Система уравнений имеет две базисные переменные
-строку не заполняем, пока система не будет приведена к единичному базису). Система уравнений имеет две базисные переменные 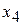 и
и 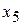 (столбцы
(столбцы 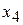 и
и 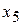 содержат единицу и нули), отмечаем это в столбце «Базис».
содержат единицу и нули), отмечаем это в столбце «Базис».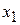
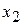
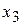
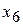
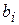
 1
1
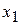 ,
, 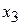 ,
, 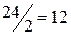 ,
, 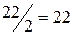 ,
, 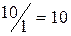 (столбец с.о.). Наименьшему симплексному отношению (10) соответствует третья строка, которая и будет разрешающей строкой. На пересечении первого столбца и третьей строки находим разрешающий элемент
(столбец с.о.). Наименьшему симплексному отношению (10) соответствует третья строка, которая и будет разрешающей строкой. На пересечении первого столбца и третьей строки находим разрешающий элемент 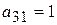 . Проведем с ним одну итерацию метода исключения переменных.
. Проведем с ним одну итерацию метода исключения переменных.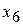
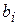
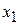 . Это означает, что система приведена к единичному базису
. Это означает, что система приведена к единичному базису 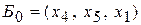 .
.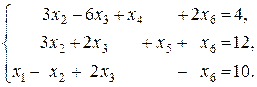
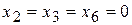 , тогда базисные переменные будут равны свободным членам
, тогда базисные переменные будут равны свободным членам 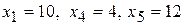 . Запишем исходное опорное решение
. Запишем исходное опорное решение 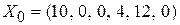 .
.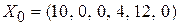 оптимальным. Если нет, то можно ли его улучшить.
оптимальным. Если нет, то можно ли его улучшить.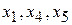 запишем нули.
запишем нули.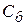
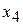
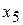
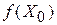 по и заполним таблицу 10:
по и заполним таблицу 10: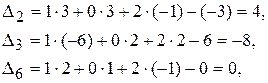
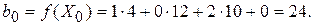
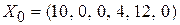 оптимальным. Из трех оценок свободных переменных в
оптимальным. Из трех оценок свободных переменных в 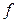 –строке
–строке 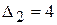 ,
, 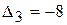 ,
, 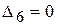 одна оценка отрицательная - это
одна оценка отрицательная - это 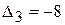 - это признак того, что решение
- это признак того, что решение 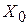 не является оптимальным. Значение целевой функции для решения
не является оптимальным. Значение целевой функции для решения 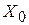 находится в правом нижнем углу симплексной таблицы - это
находится в правом нижнем углу симплексной таблицы - это 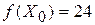 .
.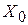 к улучшенному решению
к улучшенному решению 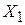 и так далее до получения оптимального решения.
и так далее до получения оптимального решения.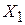 нужно от базиса
нужно от базиса 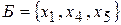 перейти к новому базису
перейти к новому базису 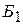 .
.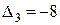 , следовательно, столбец переменной
, следовательно, столбец переменной 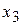 станет разрешающим, а переменная
станет разрешающим, а переменная 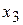 должна быть введена в базис.
должна быть введена в базис.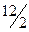 = 6;
= 6; 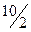 = 5 (столбец с.о.), выбираем наименьшее из них – это 5, оно находится в третьей строке, которая и станет разрешающей строкой. Значит, базисная переменная этой строки
= 5 (столбец с.о.), выбираем наименьшее из них – это 5, оно находится в третьей строке, которая и станет разрешающей строкой. Значит, базисная переменная этой строки 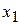 будет выведена из базиса и станет свободной. На пересечении разрешающих столбца и строки имеем разрешающий элемент
будет выведена из базиса и станет свободной. На пересечении разрешающих столбца и строки имеем разрешающий элемент  .
.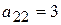 в новой таблице получится равным
в новой таблице получится равным 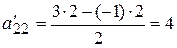 . В результате получим симплексную таблицу 14.
. В результате получим симплексную таблицу 14. 2
-1/2
2
-1/2
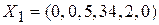 . В этом решении свободные переменные равны нулю: x 1 = 0, x 2 = 0, x 6 = 0, а базисные – свободным членам: x 3 = 5; x 4 = 34; x 5 = 2.
. В этом решении свободные переменные равны нулю: x 1 = 0, x 2 = 0, x 6 = 0, а базисные – свободным членам: x 3 = 5; x 4 = 34; x 5 = 2.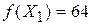 . Оно также проверяется путем подстановки компонент решения
. Оно также проверяется путем подстановки компонент решения 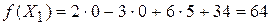 .
.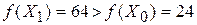 . Вычислим двумя способами приращение целевой функции при переходе от
. Вычислим двумя способами приращение целевой функции при переходе от 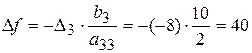 ;
; 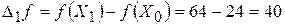 .
.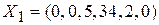 не является оптимальным, поскольку в строке оценок симплексной таблицы есть отрицательная оценка
не является оптимальным, поскольку в строке оценок симплексной таблицы есть отрицательная оценка 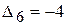 . Но
. Но 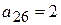 .
.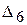 определяет переменную, вводимую в новый базис
определяет переменную, вводимую в новый базис 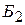 - это
- это 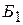 . Составим симплексные отношения для положительных элементов столбца над отрицательной оценкой
. Составим симплексные отношения для положительных элементов столбца над отрицательной оценкой 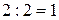 является единственным и выполняется для второй строки, в которой базисной переменной является
является единственным и выполняется для второй строки, в которой базисной переменной является 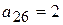 , получим симплексную таблицу 15 с базисом
, получим симплексную таблицу 15 с базисом 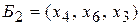 .
.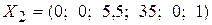 «лучше» решения
«лучше» решения 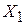 , так как
, так как 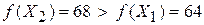 . В
. В 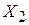 оптимальное, а значение
оптимальное, а значение 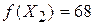 - наибольшее.
- наибольшее.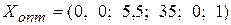 ;
; 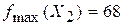 .
.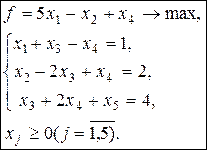 2.
2. 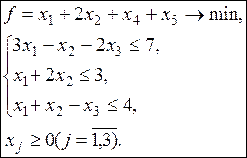
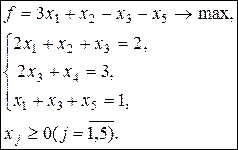 4.
4. 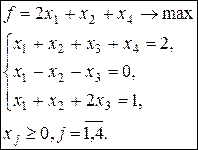
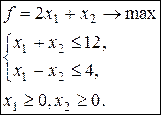 2.
2. 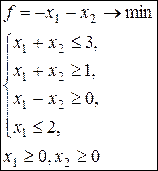 3.
3. 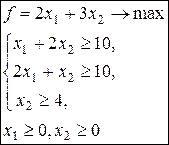
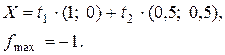 2.
2. 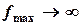 . 3. Хопт=(8, 4, 0, 0), fmax =2.
. 3. Хопт=(8, 4, 0, 0), fmax =2.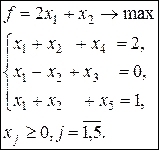 2.
2. 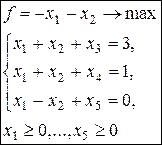 3.
3.