
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 2. Графический метод нахождения оптимального решения задачи линейного программированияСодержание книги
Поиск на нашем сайте
Примеры решения типовых задач Пример 1. Найти наибольшее и наименьшее значения функции
Решение 1. Построим область решений системы линейных неравенств.
1 О 2 x
Прямая ( Прямую ( Прямая ( Неравенства 2. Построим градиент функции 3. Параллельным движением линии уровня в направлении градиента 4. Продолжая движение линии уровня в направлении градиента Ответ:
Задачи для самостоятельного решения Задача 1. Решить графическим методом задачу линейного программирования 1) 4)
Нахождение оптимального решения экономических задач линейного программирования Примеры решения типовых задач Пример 2. Задача о рационе Решить экономическую задачу линейного программирования графическим методом. При составлении суточного рациона кормления скота можно использовать свежее сено не более 50 кг и силос не более 85 кг. Рацион должен содержать не менее 30 кормовых единиц, 1000 г белка, 100 г кальция и 80 г фосфора. Определить оптимальный рацион, исходя из условия минимума себестоимости. В таблице 4 приведены данные о содержании указанных компонентов в 1 кг каждого корма и себестоимость этих кормов. Таблица 7
Решение Этап 1. Составление математической модели задачи. Обозначим через Количество кормовых единиц в рационе можно выразить суммой Ограничения по содержанию в рационе белка, кальция и фосфора имеют вид:
Себестоимость рациона в принятых обозначениях можно выразить формулой Математическая постановка задачи: найти неотрицательные значения переменных
и при которых целевая функция принимает наименьшее значение
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 162; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.21.101 (0.007 с.) |
|||||||||||||||||||||||||||

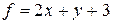 в области решений системы линейных неравенств
в области решений системы линейных неравенств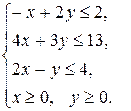
 у
у
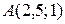
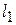
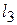
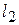
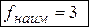
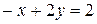 , точки для построения
, точки для построения  и
и 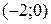 . Так как
. Так как 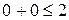 верно, то полуплоскость обращена в сторону точки
верно, то полуплоскость обращена в сторону точки 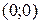 .
.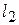 )
) 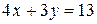 строим по точкам
строим по точкам 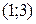 и
и 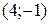 ; неравенство
; неравенство 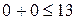 верное, полуплоскость направлена к началу координат.
верное, полуплоскость направлена к началу координат.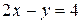 построена по точкам
построена по точкам 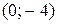 и
и 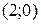 ; полуплоскость обращена в сторону
; полуплоскость обращена в сторону 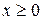 и
и  показывают, что искомая область (пересечение всех полуплоскостей) находится в первой координатной четверти.
показывают, что искомая область (пересечение всех полуплоскостей) находится в первой координатной четверти.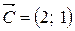 с началом в точке
с началом в точке 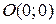 . Перпендикулярно градиенту построим одну из линий уровня.
. Перпендикулярно градиенту построим одну из линий уровня. найдем точку «входа» линии уровня в область – это точка О(0,0). Вычислим значение функции в этой точке:
найдем точку «входа» линии уровня в область – это точка О(0,0). Вычислим значение функции в этой точке: 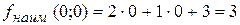 .
.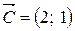 , найдем точку «выхода» линии уровня из области – это точка А. Для определения ее координат решим систему уравнений прямых
, найдем точку «выхода» линии уровня из области – это точка А. Для определения ее координат решим систему уравнений прямых 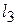 :
: 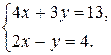 Решение системы уравнений
Решение системы уравнений 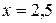 и
и 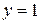 . Вычислим значение функции в точке
. Вычислим значение функции в точке 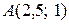 :
: 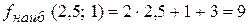 .
.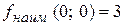 ,
, 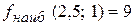 .
.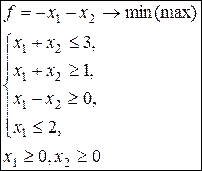 2)
2) 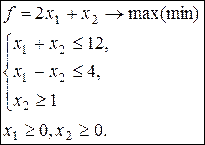 3)
3) 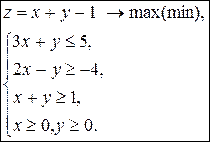
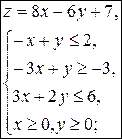 5)
5) 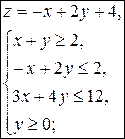 6)
6) 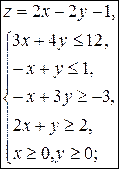 7)
7) 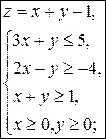
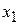 и
и 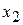 количество кг сена и силоса, которое предполагается включить в рацион. Естественно, что
количество кг сена и силоса, которое предполагается включить в рацион. Естественно, что 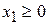 ,
, 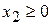 . Из условия задачи следует, что
. Из условия задачи следует, что 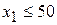 (кг);
(кг); 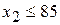 (кг).
(кг).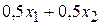 , что должно быть, по условию, не меньше 30:
, что должно быть, по условию, не меньше 30: 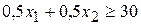 (ед.), или
(ед.), или 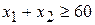 .
.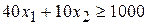 (г), или
(г), или 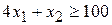 (для белка);
(для белка);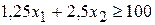 (г), или
(г), или 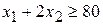 (для кальция);
(для кальция); 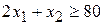 (г) (для фосфора).
(г) (для фосфора).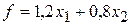 (руб.). Итак, математическая модель задачи построена.
(руб.). Итак, математическая модель задачи построена.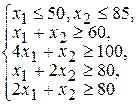
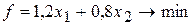 .
.


