
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Диаграмма И. И никурадзе. Ее практическое назначение. Зоны сопротивления. Гладкие и шероховатые трубы.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Основной расчетной формулой для потерь напора при турбулентном течении жидкости в круглых трубах является эмпирическая формула, называемая формулой Вейсбаха-Дарси и имеющая следующий вид: Область ламинарного режима (I). В области ламинарного режима (т.е. при Re < 2300, чему соответствует lg Re < 3,36) опытные точки, независимо от шероховатости стенок, уложились на одну прямую линию I. Следовательно, здесь λ зависит только от числа Рейнольдса и не зависит от шероховатости, т.е. λ =f (Re). Остальные участки кривых (II, III, IV) относятся к турбулентному движению.В области перехода от ламинарного движения к турбулентному Re = 2000-4000 (3,3< lgRe< 3,6) наблюдается большой разброс опытных точек и кривая между I и II рис. 4.11 проведена условно. Область гидравлически гладких труб (II). В этой области опытные точки для труб с различной шероховатостью располагаются в некотором диапазоне чисел Re на одной прямой II, отрываясь от нее в сторону возрастания коэффициента λ тем раньше, чем больше шероховатость стенок. Таким образом, при некоторых условиях шероховатость не оказывает влияния на потери напора также и при турбулентном движении, т.е. и здесь λ =f (Re). Область смешанного трения (III). Здесь каждая кривая относится к определенному значению относительной шероховатости и величина также меняется с изменением числа Рейнольдса, т.е. коэффициент гидравлического сопротивления зависит от числа Re. Область «вполне шероховатых труб» (IV). При увеличении числа Re кривые области III переходят в линии, параллельные оси lg Re, т,е. коэффициент λ в этой области не зависит от числа Re и определяется только относительной шероховатостью. Полуэмпиричекая теория турбулентности позволяет предложить выражение для коэффициента λ, исходя из распределения скорости в живых сечениях потока.
Можно вывести следующие полуэмпирические формулы Прандтля-Никурадзе из логарифмического закона распределения скоростей: Для гладких труб
|
|||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 498; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.52.206 (0.01 с.) |

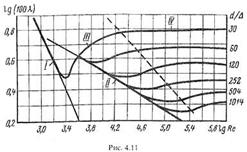
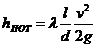 . Различие заключается лишь в значениях коэффициента гидравлического трения λ. Этот коэффициент зависит от числа Рейнольдса Re и от безразмерного геометрического фактора - относительной шероховатости Δ/d (или Δ/r0, где r0 - радиус трубы). Результаты опытов Никурадзе представлены графически на рис. 4.11 На этом графике по горизонтальной оси отложены величины lgRe, а по вертикальной оси — lg(l00 λ). Кривые построены по данным опытов с трубами относительной шероховатости от ε=∆/d= 0,001 (самая нижняя кривая) до ε=0,033 (самая верхняя кривая). Существуют четыре различные области.
. Различие заключается лишь в значениях коэффициента гидравлического трения λ. Этот коэффициент зависит от числа Рейнольдса Re и от безразмерного геометрического фактора - относительной шероховатости Δ/d (или Δ/r0, где r0 - радиус трубы). Результаты опытов Никурадзе представлены графически на рис. 4.11 На этом графике по горизонтальной оси отложены величины lgRe, а по вертикальной оси — lg(l00 λ). Кривые построены по данным опытов с трубами относительной шероховатости от ε=∆/d= 0,001 (самая нижняя кривая) до ε=0,033 (самая верхняя кривая). Существуют четыре различные области.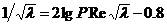 , Для вполне шероховатых труб
, Для вполне шероховатых труб 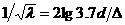 . Результаты обобщения большого числа опытов показали, что λ является функцией двух безразмерных параметров числа Рейнольдса, отражающего влияние вязкости и скорости движения жидкости и относительной шероховатости ε=∆/d, характеризующего влияние поверхности стенок, т.е. λ=f(Re, ∆/d).
. Результаты обобщения большого числа опытов показали, что λ является функцией двух безразмерных параметров числа Рейнольдса, отражающего влияние вязкости и скорости движения жидкости и относительной шероховатости ε=∆/d, характеризующего влияние поверхности стенок, т.е. λ=f(Re, ∆/d).


