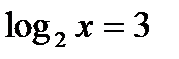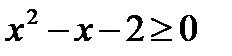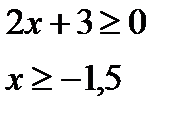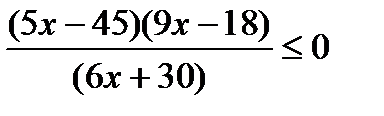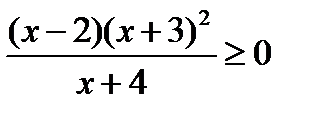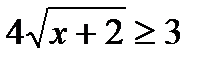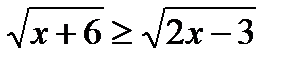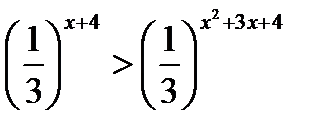Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математика (включая алгебру и начала математического анализа, геометрию)Содержание книги
Поиск на нашем сайте
Практических работ по учебной дисциплине Математика (включая алгебру и начала математического анализа, геометрию) общеобразовательного цикла программы подготовки специалистов среднего звена по специальностям 23.02.03. Техническое обслуживание и ремонт автомобильного транспорта 35.02.08 Электрификация и автоматизация сельского хозяйства 35.02.06 Технология производства и переработки сельскохозяйственной продукции
г. Миллерово 2020
Рассмотрено и одобрено на заседании цикловой комиссии общеобразовательного, общего гуманитарного социально-экономического и естественнонаучного циклов дисциплин Протокол № 1 от «31» августа 2020 г Председатель ____________ И.Н.Куркина
Организация-разработчик: государственное бюджетное профессиональное образовательное учреждение Ростовской области «Миллеровский техникум агропромышленных технологий и управления (ДСХТ)»
Разработчик: Бондаренко Г.И., преподаватель ГБПОУ РО «МТАТиУ (ДСХТ)»
СОДЕРЖАНИЕ
Введение УВАЖАЕМЫЙ ОБУЧАЮЩИЙСЯ! Методические указания по дисциплине «Математика» (включая алгебру и начала математического анализа, геометрию) для выполнения практических работ созданы Вам в помощь для работы на занятиях, подготовки к ним, правильного составления проектов документов. Приступая к выполнению практической работы, Вы должны внимательно прочитать цель занятия, ознакомиться с краткими теоретическими и учебно-методическими материалами по теме практической работы, ответить на вопросы для закрепления теоретического материала. Наличие положительной оценки по практическим работам необходимо для получения зачета по дисциплине и допуска к дифференцированному зачету и экзамену, поэтому в случае отсутствия на уроке по любой причине или получения неудовлетворительной оценки за практическую работу Вы должны найти время для ее выполнения или пересдачи. Внимание! Если в процессе подготовки к практическим работам или при решении задач у Вас возникают вопросы, разрешить которые самостоятельно не удается, необходимо обратиться к преподавателю для получения разъяснений или указаний в дни проведения дополнительных занятий. Время проведения дополнительных занятий можно узнать у преподавателя или посмотреть на двери его кабинета.
Желаем Вам успехов!!! АЛГЕБРА Примеры и последовательность выполнения заданий Пример 1. Возвести в степень Решение
Пример 2. Вычислить Решение
Пример 3. Упростить выражение. а) Решение
б) Решение
Пример 4. Избавиться от иррациональности в знаменателе. Чтобы уничтожить иррациональность в знаменателе, нужно знаменатель и числитель дроби умножить на такое выражение, которое в произведении со знаменателем дает рациональное выражение в знаменателе.
а) Решение
б) Решение
Пример 5. Представить в виде степени с основанием x (x>0)
Решение
Выполнить следующие задания. Задание 1. Возвести в степень Задание 2. Вычислить а) Задание 3. Упростить выражение а) Задание 4. Избавиться от иррациональности в знаменателе. а) Задание 5. Представьте в виде степени с основанием х (х>0) а) Задание 6. Вычислить значение выражения.
АЛГЕБРА Примеры и последовательность выполнения заданий. Пример 1. Вычислить. Решение. Пример 2. Вычислить. а) Решение. б) Решение. Решение. Пример 4. Вычислить. Решение.
Пример 5. Решить уравнение. Решение.
Выполнить следующие задания. Задание 1. Вычислить. a) b) c) d) e) f) Задание 2. Решить уравнение a) Задание 3. Упростить выражение a) Задание 4. Упростить выражение
Задание 5. Вычислить
АЛГЕБРА Примеры и последовательность выполнения заданий. Пример 1. Упростить выражение. а) Решение. Обозначим
Ответ: Б) Решение. Выделим общий множитель в числителе и знаменателе первой дроби данного выражения. Для этого представим числитель в виде
Пример 2. Проверить справедливость равенства.
Решение. Рассмотрим равенство
Так как a2 = b2, то a = b, т.е. заданное равенство справедливо. Выполнить следующие задания. Задание 1. Вычислить.
Задание 2. Упростить выражение. а) б) Задание 3. Докажите, что выражение Задание 4. Найдите lgx, если ОСНОВЫ ТРИГОНОМЕТРИИ Тема. Преобразования простейших тригонометрических выражений. Примеры и последовательность выполнения заданий. Пример 1. Вычислить а) Решение А) Б) Пример 2.
Найти: а) Решение А) Из основного тригонометрического тождества получим:
Так как Б) Пример 3. Упростить выражение Решение
Пример 4. Доказать тождество Доказательство
Выполнить следующие задания Задание 1. Вычислить а) Задание 2.
Найти: а) Задание 3. Упроститьвыражение Задание 4. Доказать тождество. а) ОСНОВЫ ТРИГОНОМЕТРИИ Примеры и последовательность выполнения заданий. Рекомендации по решению тригонометрических уравнений. 1. Если аргументы функций одинаковые, попробовать получить одинаковые функции, использовав формулы без изменения аргументов. 2. Если аргументы функций отличаются в два раза, попробовать получить одинаковые аргументы, использовав формулы двойного аргумента. 3. Если аргументы функций отличаются в четыре раза, попробовать их привести к промежуточному двойному аргументу.
4. Если в уравнении есть числовое слагаемое (множитель), то его можно представить в виде значений функции угла. Например:
Примеры и последовательность выполнения заданий. Пример 1. Решить простейшее тригонометрическое уравнение. Используя блок-схему для решения тригонометрических уравнений, получим
Пример 2. Тригонометрические уравнения, приводимые к квадратным: A sin2 х + В sin х + С =0 или A sin2 х + В cos х + С =0
Пример 3. а) Однородное тригонометрическое уравнение первого порядка б) Однородное тригонометрическое уравнение второго порядка А sin2 х + В sinх cos х + С cos2х = 0. Разделив обе части уравнения на cos2 x ≠ 0, получим уравнение вида А tg 2x + В tg x + С = 0. Выполнить следующие задания УРАВНЕНИЯ И НЕРАВЕНСТВА Примеры и последовательность выполнения заданий. Пример 1. Решение
Проверка: Ответ: x = -1
Решение Обозначая y2 – 5y + 6 = 0, корни этого уравнения: y1 = 2, y2 = 3. Таким образом, исходное уравнение эквивалентно двум уравнениям вида:
решения которых: x = 4 и x = 8. Ответ: x = 4, x = 8. |
| ||||||||||||||||||||||||||||||||||||||||||||
Выполнить следующие задания
Задание 1. Решить уравнение.
а) 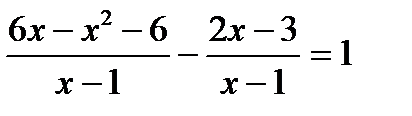 б)
б) 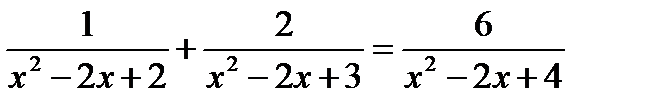 в)
в) 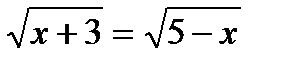 г)
г) 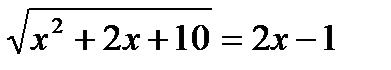 д)
д) 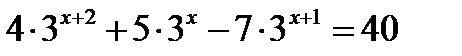 е)
е) 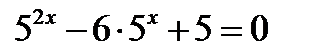 ж)
ж) 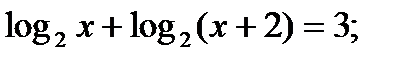 з)
з) 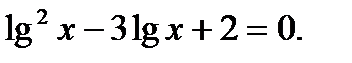
| Задание 2. Решить систему уравнений
а) 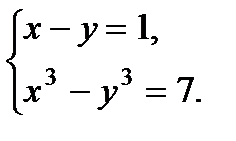 б)
б) 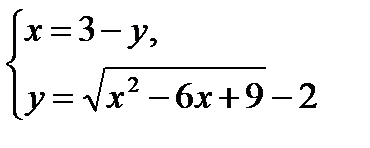 в)
в) 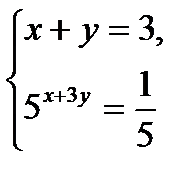 г)
г) 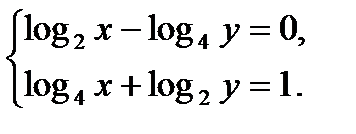
|
УРАВНЕНИЯ И НЕРАВЕНСТВА
|
|
Примеры выполнения заданий.
Пример 1. Решить неравенство 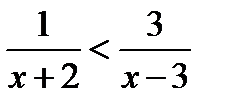 .
.
Решение.
Приведем неравенство к стандартному виду:
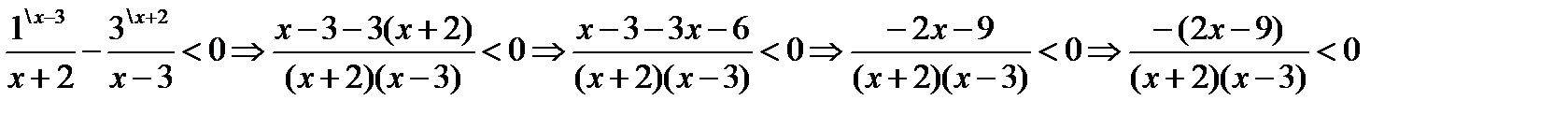
Найдем критические точки:
1. 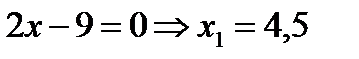
2. 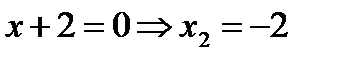
3. 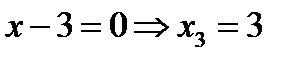
Построим числовую прямую, полученные точки разобьют ее на интервалы. Определим знак на каждом из интервалов:
| + |
| + |
| 3 4,5 |
| -2 |
Так как неравенство < 0, следовательно, выберем те промежутки, которые имеют знак минус. Решениями неравенства являются следующие промежутки:
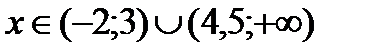
Пример 2. Решить иррациональное неравенство 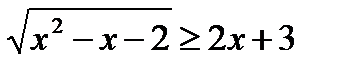
Решение.
Исходное неравенство равносильно системе неравенств:
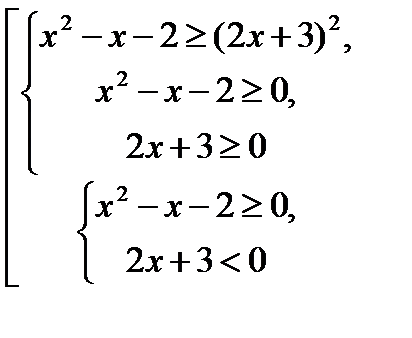 Решим каждое неравенство в отдельности:
Решим каждое неравенство в отдельности:
1. 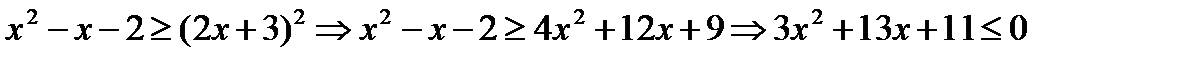
| + |
| + |
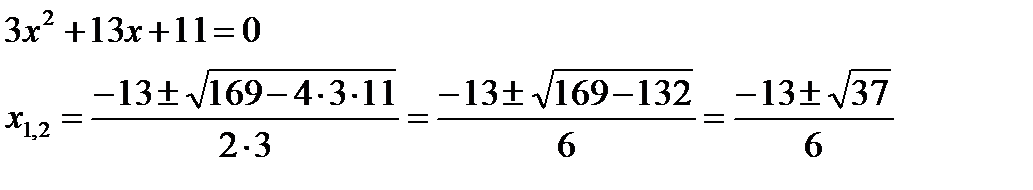
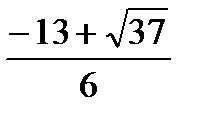
|
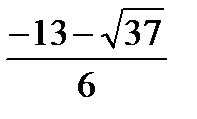
|
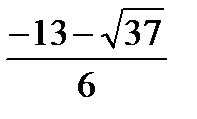 ;
; 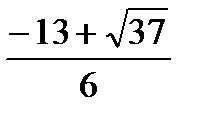 ]
]
| + |
| + |
| -1 2 |

Решениями второго неравенства являются промежутки 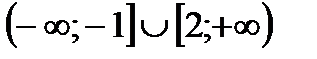
Запишем найденные решения в систему неравенств:
| -1,5 -1 2 |
| -1 2 |
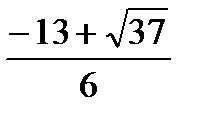
|
| -1,5 |
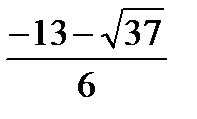
|

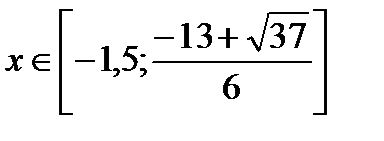
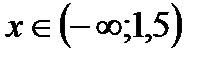
Ответ. 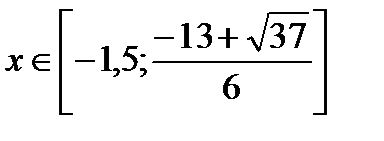 ,
, 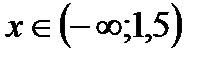
Пример 3. 
Решение.
Так как 2 > 1, функция возрастает, следовательно
x2 – 3 x +3 > x2 – 2 x +5
-3 x + 2 x > 5 – 3
- x > 2
x < 2
Пример 4. 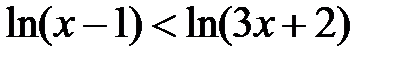
Решение.
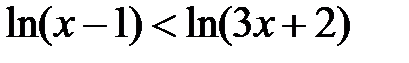 , так как е > 1, то функция возрастающая, следовательно, получим систему неравенств:
, так как е > 1, то функция возрастающая, следовательно, получим систему неравенств:
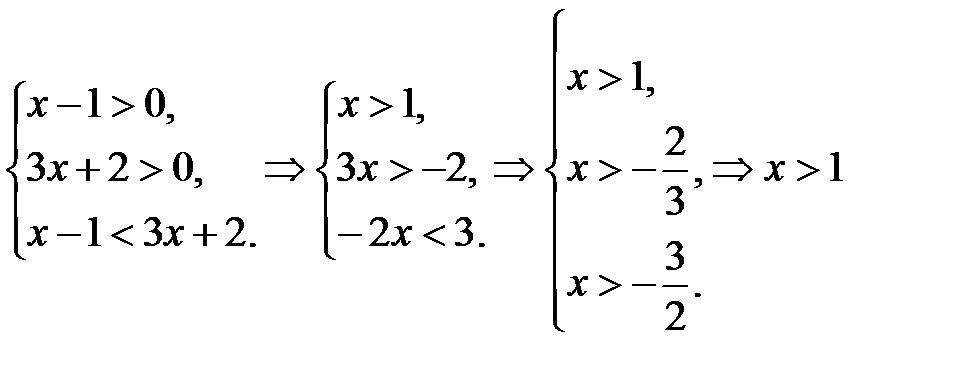
Ответ: x > 1.
Выполнить следующие задания
Решить неравенства.
Задание 1.
Задание 2.
-
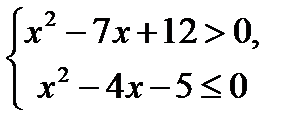
-
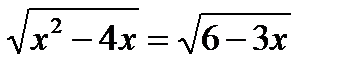
- 9×3x - 1 + 3x < 36
-
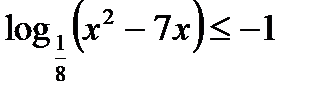
Тема. Производная.
Примеры выполнения заданий.
Задание. Исследовать функцию 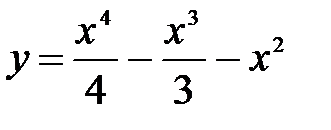 и построить ее график.
и построить ее график.
Решение.
1) Область определения – множество действительных чисел.
2) Точки пересечения с осями координат:
если x = 0, то y = 0 – точка А (0,0);
если y = 0, то решим уравнение 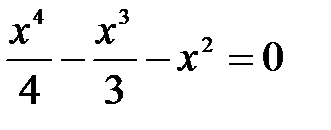 .
.
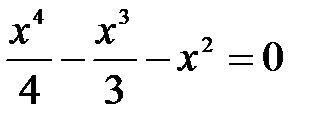
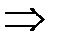
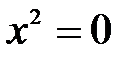 и
и 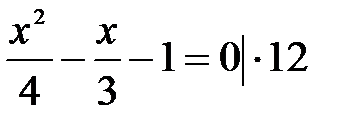
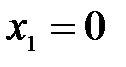
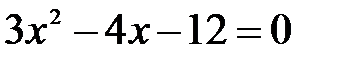
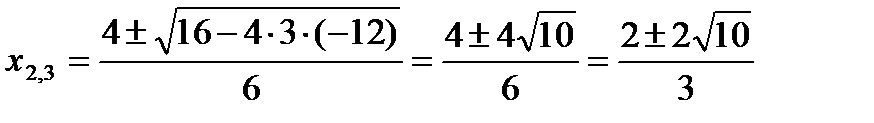
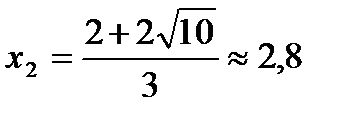 и
и 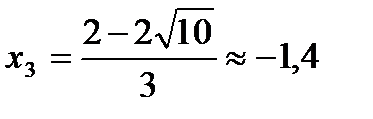
Получили еще две точки В (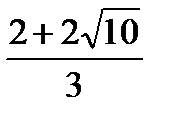 ; 0) и С (
; 0) и С (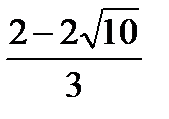 ; 0).
; 0).
3) Четность, нечетность: 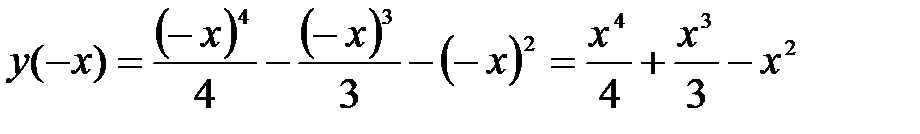 - функция не является ни четной, ни нечетной.
- функция не является ни четной, ни нечетной.
4) Находим производную. 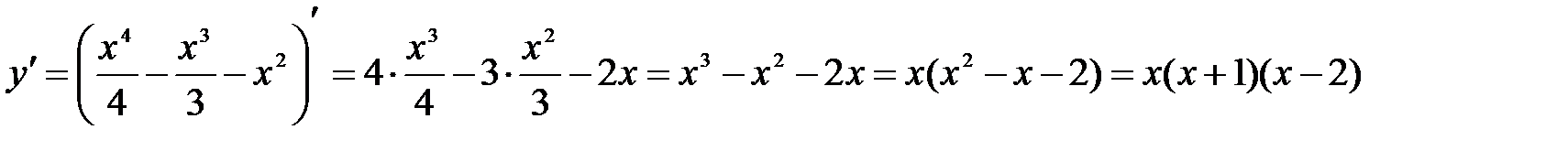 .
.
5) Стационарные точки. Приравняем производную к нулю: 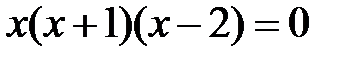 , получим x = -1, x = 0, x= 2 – стационарные точки.
, получим x = -1, x = 0, x= 2 – стационарные точки.
6)
| - 1 0 2 |
Промежутки возрастания и убывания. Найденные точки разбивают числовую прямую на четыре промежутка, определим знак производной на этих промежутках.
7) Точки экстремума. x = -1, x = 2 – точки минимума; x = 0 – точка максимума.
8) Выпуклость и точки перегиба.
Найдем вторую производную: 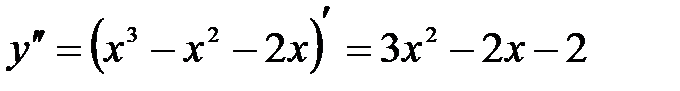 .
.
Найдем точки перегиба: 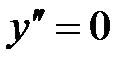 ;
;
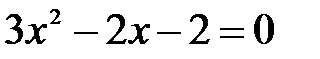
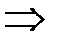
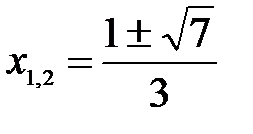
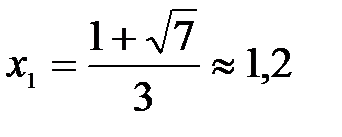 и
и 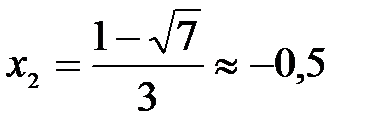 - точки перегиба
- точки перегиба
| ≈ - 0,5 ≈ 1,2 |
Определим знак второй производной на интервалах:
|
|
9) Составим таблицу.
| x | x < -1 | - 1 | – 1 < x < 0 | 0 | 0 < x < 2 | 2 | x > 2 | 3 |
| f ‘(x) | - | 0 | + | 0 | - | 0 | + | |
| f(x) | -5/12 min | 0 max | -8/3 min | 9/4 |
Выполнить следующие задания.
Задание 1. Исследовать функцию и построить ее график.
а) 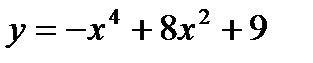 б)
б) 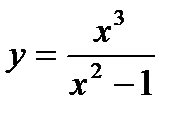
Задание 2. Найти наибольшее и наименьшее значения функций на указанном промежутке
а) у = (х-3)2(х-2) на отрезке [1;4]
б) у =1/3 х3 + х2 на отрезке [-4;1]
в) у = - 2/3 х3 + 2х – 4/3 на отрезке [-1,5;1,5]
Примеры выполнения заданий.
При непосредственном интегрировании следует пользоваться таблицей интегралов. Интегрируя функции, содержащие переменную в знаменателе дроби или под знаком радикала, нужно вводить степень с отрицательным или дробным показателем.
Пример 1. 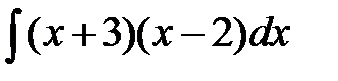
Решение
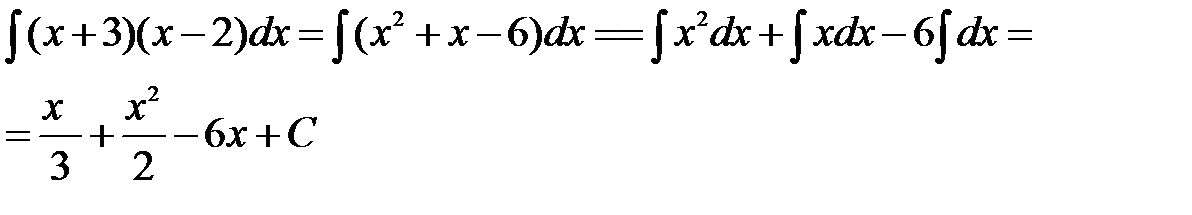
Пример 2. 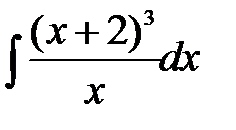
Решение
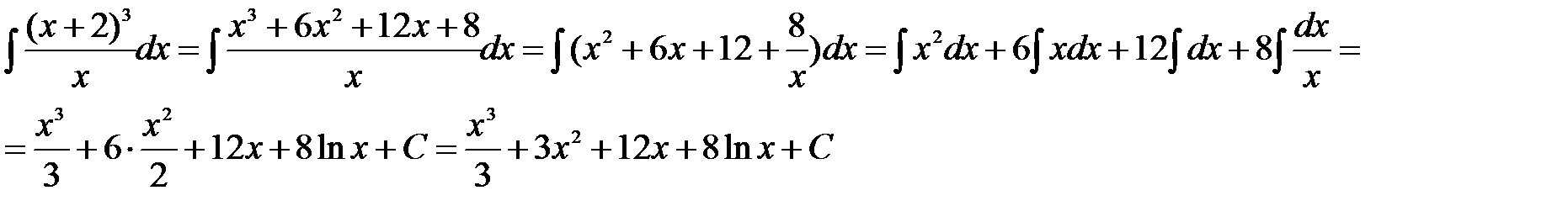
Для вычисления значения определенного интеграла используем формулу Ньютона-Лейбница. Берем неопределенный интеграл и находим любую первообразную, затем вычисляем разность ее значений, соответствующих верхнему и нижнему пределов.
Пример 3. 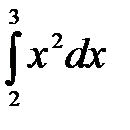
Решение
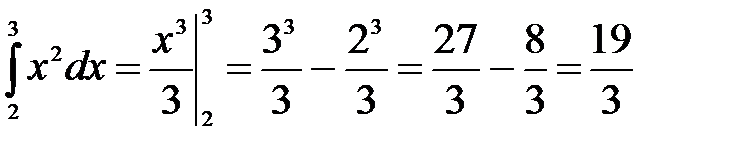
Пример 4. 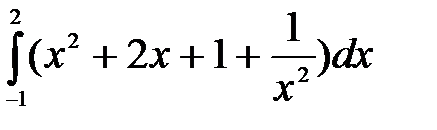
Решение
| y |
| x |
| x = -3 |
| x = 2 |
| А(0; 2) |
| B(4; 0) |
| S |
| Рис. 1 |
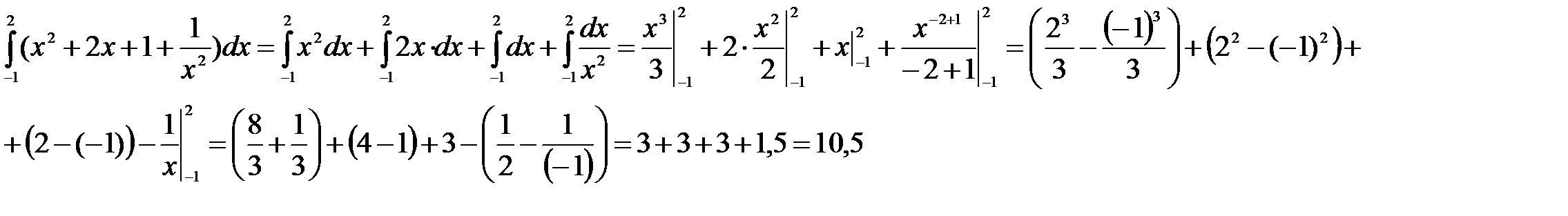 Пример 5. Вычислить площади фигур, ограниченных линиями y = -0,5 x + 2, y = 0, x = -3 и x = 2.
Пример 5. Вычислить площади фигур, ограниченных линиями y = -0,5 x + 2, y = 0, x = -3 и x = 2.
Решение. Выполним построение фигуры. Строим прямую y = - 0,5 x + 2 по двум точкам. Найдем эти точки. Пусть x = 0, тогда y = 2. Получили первую точку А(0; 2). Пусть y = 0, тогда x = 4. Получили вторую точку В(4; 0).
Т.о. f(x) = -0,5 x + 2, а = -3, b = 2, находим площадь по формуле 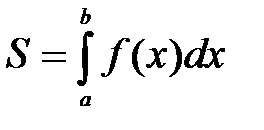 :
:
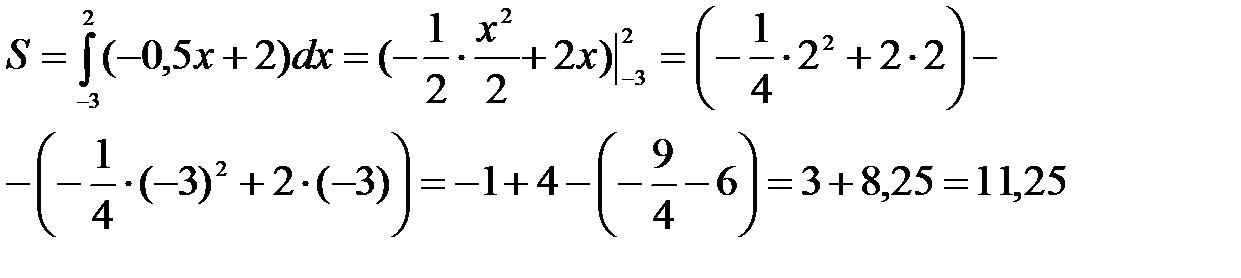
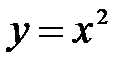 Ответ: S = 11, 25 (кв. ед.)
Ответ: S = 11, 25 (кв. ед.)
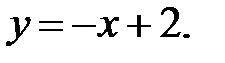 Пример 4. Вычислите площадь фигуры, ограниченной линиями и
Пример 4. Вычислите площадь фигуры, ограниченной линиями и
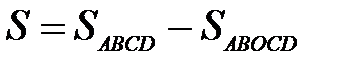 Решение
Решение
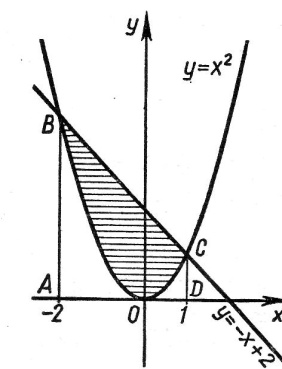
Для нахождения пределов интегрирования решаем уравнение:
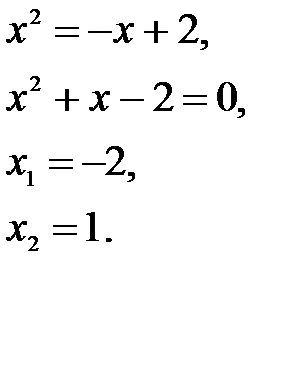
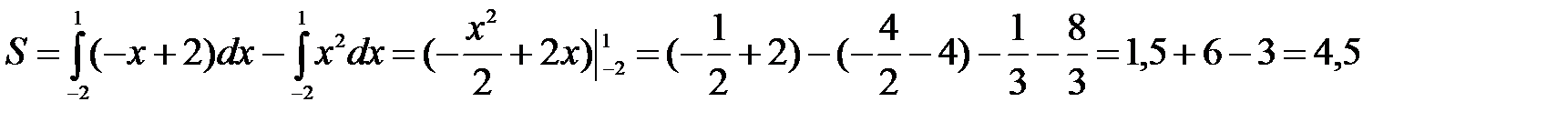 Искомая площадь равна:
Искомая площадь равна:
Выполнить следующие задания.
Задание 1. Найти неопределенный интеграл.
а) 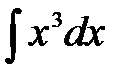 б)
б) 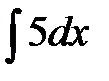
в) 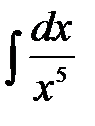 г)
г) 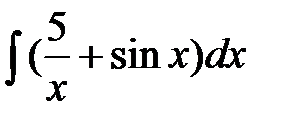 д)
д) 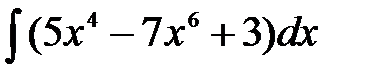
Задание 2. Вычислить определенный интеграл.
а) 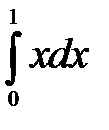 б)
б) 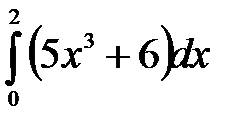 в)
в) 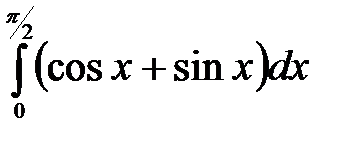 г)
г) 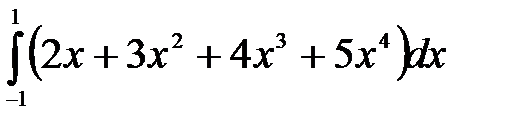 д)
д) 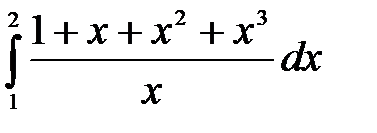
Задание 3. Найти площадь фигуры, ограниченной линиями:
а) Найти площадь фигуры, ограниченной осью Ох и параболой: у = 4 – х2.
б) Найти площадь фигуры, ограниченной параболами 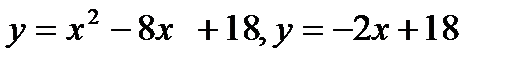
Геометрия
Примеры и последовательность выполнения заданий.
Пример 1. В 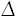 ABC вершины A (2; 0; 3), B (0; 1; 2), C (1; 2; 4). Определить вид
ABC вершины A (2; 0; 3), B (0; 1; 2), C (1; 2; 4). Определить вид 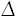 ABC.
ABC.
Решение.
Сравним длины сторон: AB = 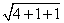 =
= 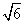
AC= 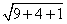 =
= 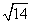
BC= 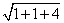 =
= 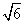
AC >AB = BC – 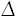 ABC – непрямоугольный, т.к. AC2 ≠ AB2 + BC2 => 14 ≠ 6 + 6
ABC – непрямоугольный, т.к. AC2 ≠ AB2 + BC2 => 14 ≠ 6 + 6
AC2 = AB2 + BC2 - 2AB ∙ BC ∙cosα (теорема косинусов)
14 = 12 – 12 cosα
cosα = – 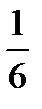 < 0 => α – тупой
< 0 => α – тупой
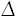 ABC – равнобедренный, тупоугольный.
ABC – равнобедренный, тупоугольный.
Пример 2. Докажите, что четырехугольник ABCD является ромбом, если A(6; 7; 8), B(8; 2; 6), C(4; 3; 2), D(2; 8; 4).
Решение.
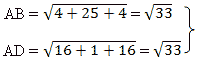 смежные стороны равны
смежные стороны равны
Найдем середину отрезка BD и AC:
B (8; 2; 6) D (2; 8; 4) x0 = 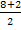 = 5 y0 = = 5 y0 = 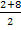 = 5 z0 = = 5 z0 = 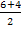 = 5 = 5
| A (6; 7; 8) C (4; 3; 2) x' = 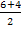 = 5 y' = = 5 y' = 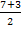 = 5 z' = = 5 z' = 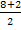 = 5 = 5
|
Середина отрезков BD и AC точка O(5;5;5). Диагонали точкой пересечения делятся пополам в параллелограмме. Четырехугольник ABCD – ромб. Проверим, не квадрат ли это?
Решение: BD = 
BD2 ≠ AB2 + AD2 76 ≠ 33 + 33 => ABCD – не квадрат
Пример 3. Выяснить при каких значениях m и n данные векторы коллинеарные: 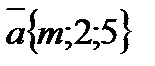 и
и 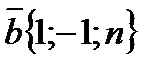 .
.
Решение.
У коллинеарных векторов соответствующие коэффициенты пропорциональны. Запишем соответствующую пропорцию, из которой найдем m и n:
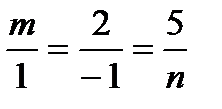 , откуда
, откуда 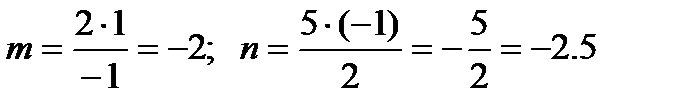
Ответ: m = -2, n = -2.5.
Выполнить задания
Задание 1.
Дан треугольник АВС с вершинами А(11;-2;-9), В(2;6;-4), С(8;-6;-8). Найдите длину медианы АК.
Задание 2.
а) Найдите значения m и n, при которых векторы 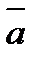 и
и 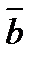 коллинеарные, если
коллинеарные, если 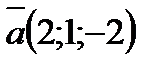 и
и 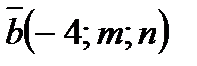 .
.
б) Даны векторы 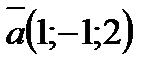 и
и 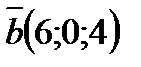 . Найдите
. Найдите 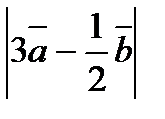 . Сравните с прямым углом угол между векторами
. Сравните с прямым углом угол между векторами 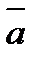 и
и 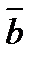 .
.
в) Найдите угол между векторами 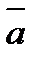 и
и 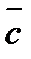 , если
, если 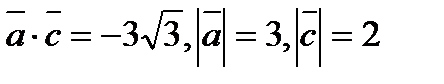 .
.
г) Даны векторы  ;
; 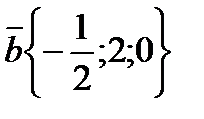 ;
; 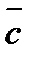
 ;
;



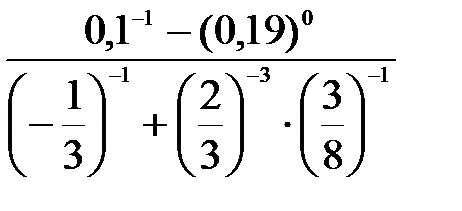
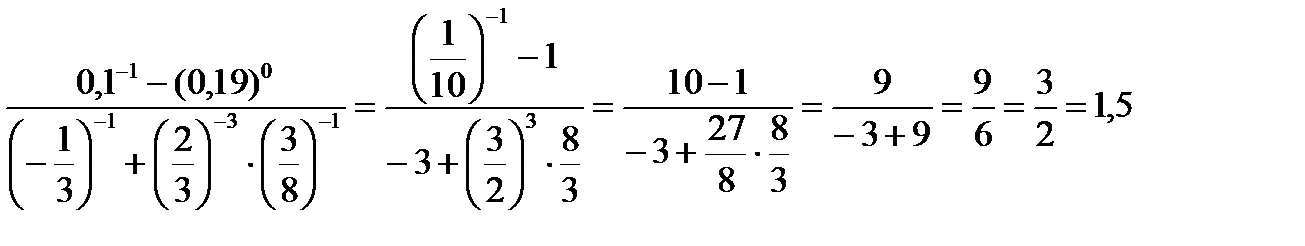
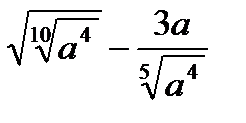
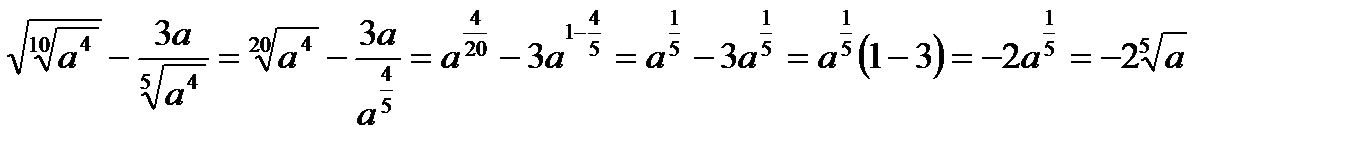

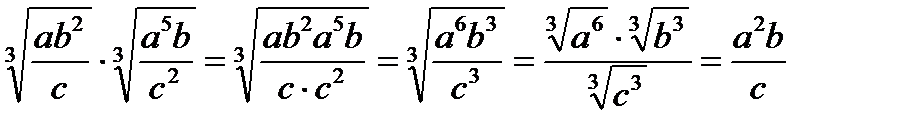
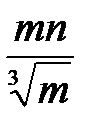
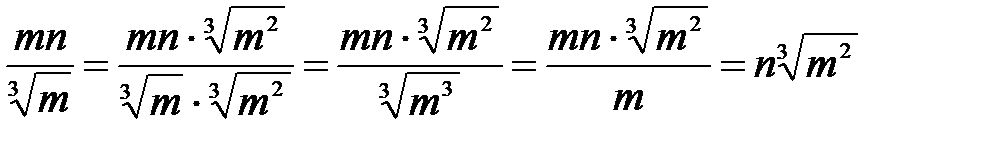
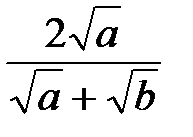
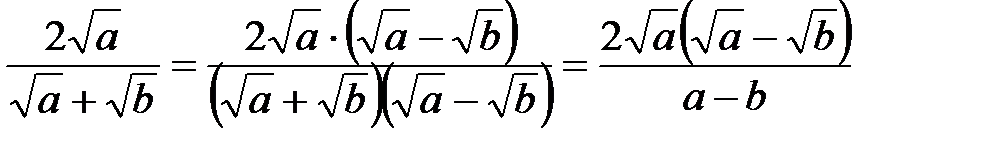
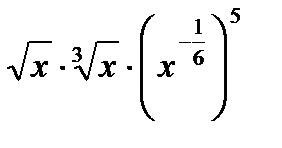
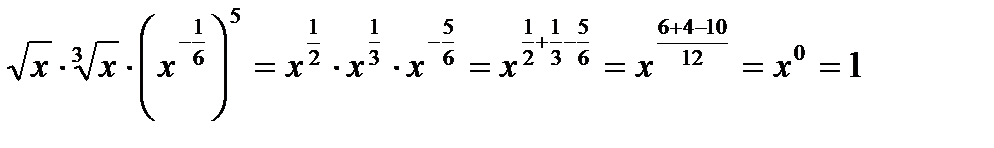
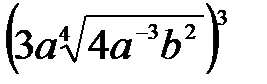
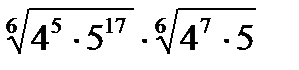 б)
б) 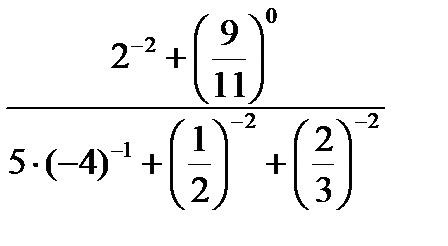
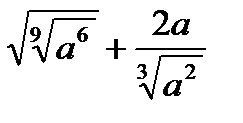 б)
б) 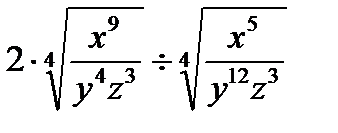
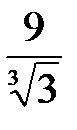 б)
б) 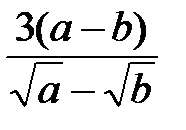
 ; б)
; б) 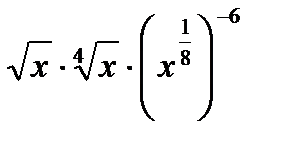
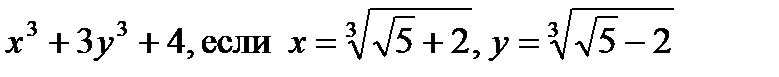

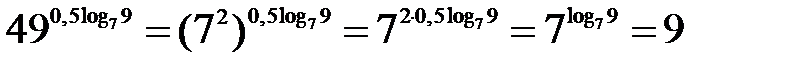



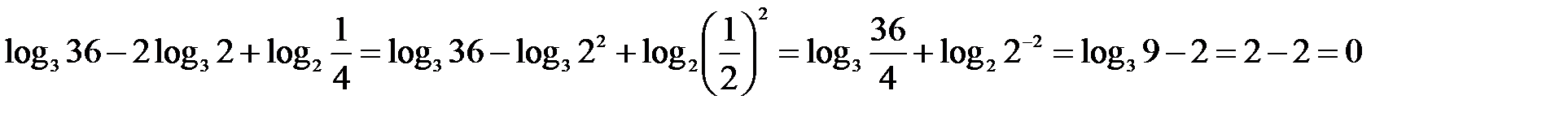 Пример 3. Упростить выражение.
Пример 3. Упростить выражение. 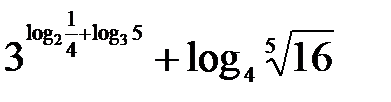


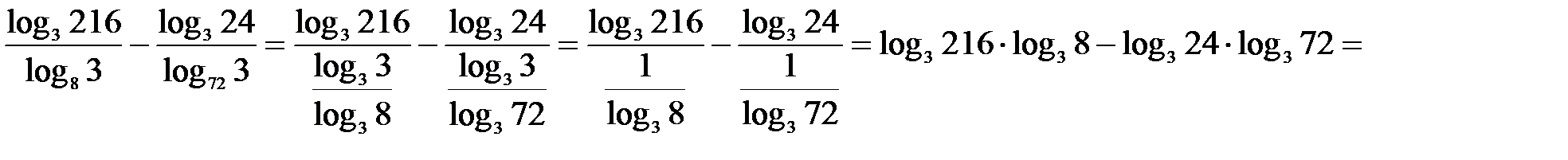
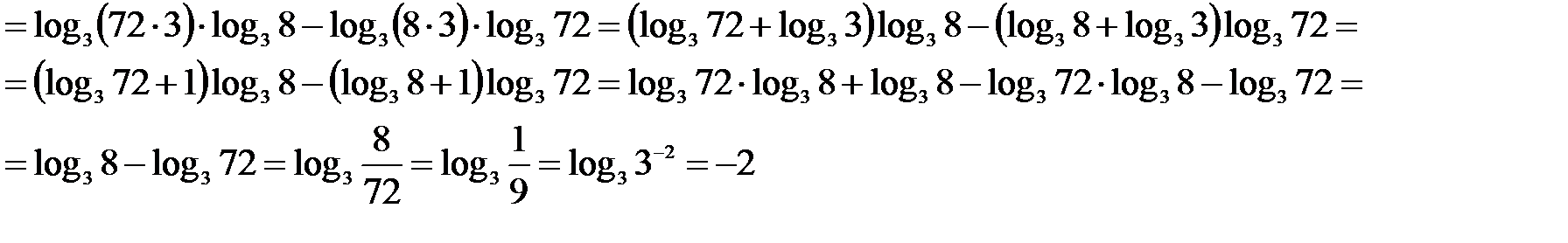
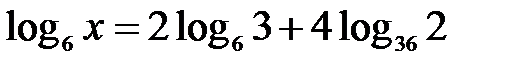
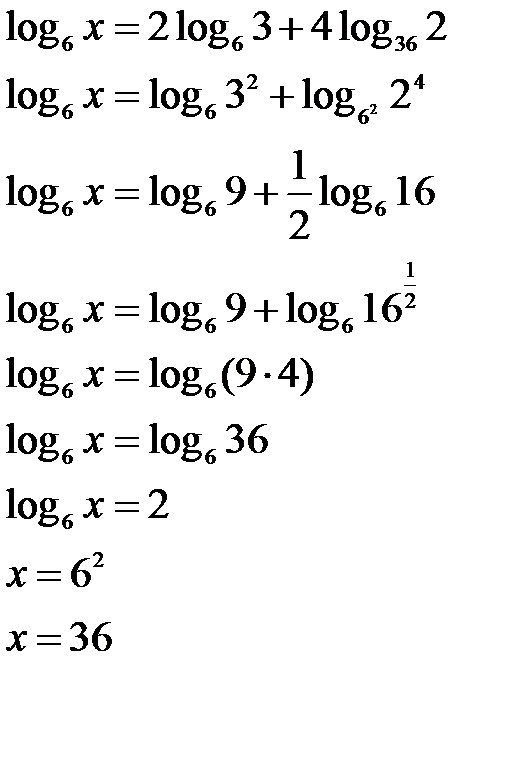
 ;
; 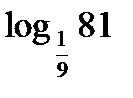 ;
; 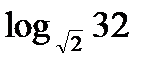 ;
; 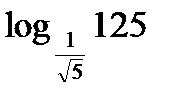
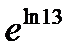 ;
; 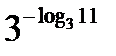 ;
; 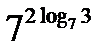 ;
; 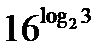
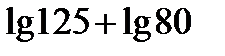 ;
; 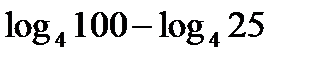 ;
; 
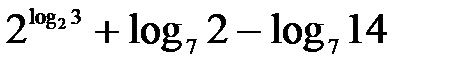
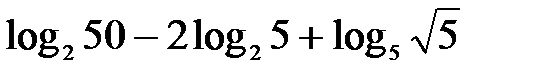
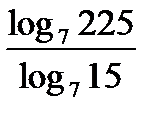 ;
; 
 b)
b) 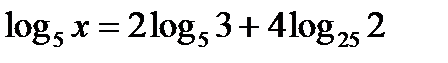
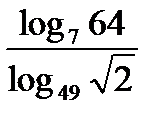 b)
b) 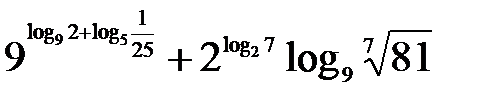
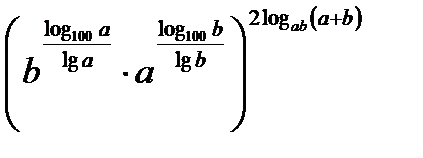
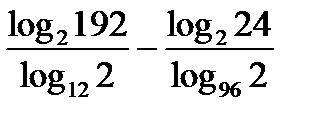
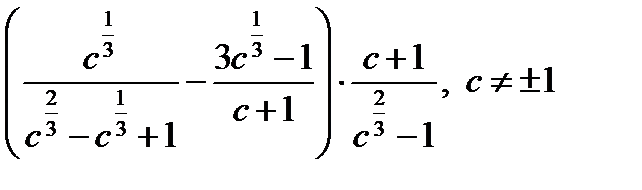
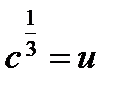 , тогда
, тогда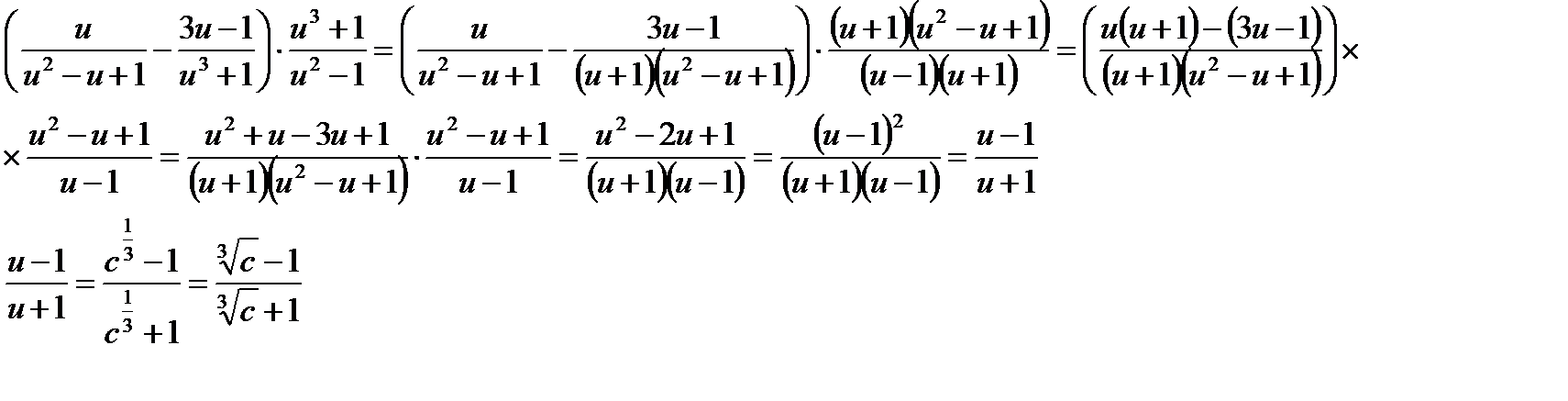
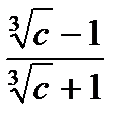
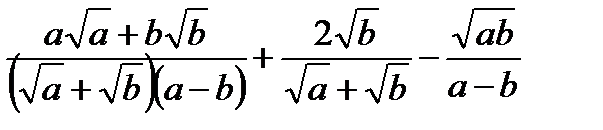
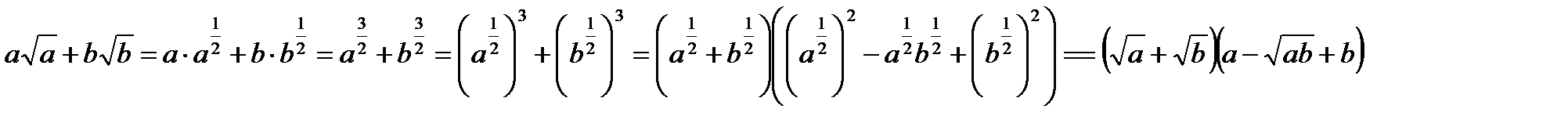
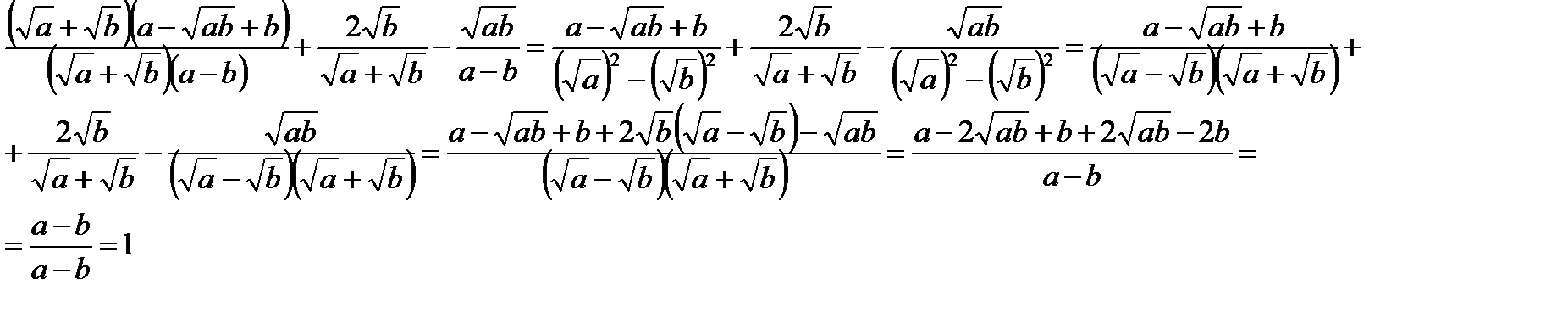
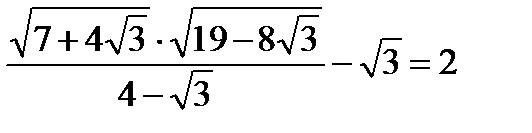
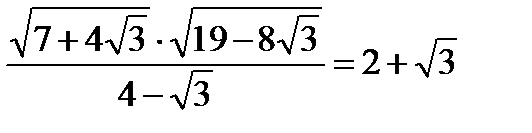 . Очевидно, что если оно верно, то верно и заданное равенство. Пусть
. Очевидно, что если оно верно, то верно и заданное равенство. Пусть 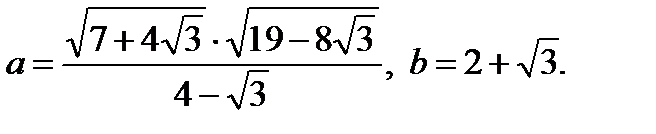 Проанализировав выражения, получим, что a> 0, b> 0. Если при этом выполняется равенство a2 = b2, то a = b. Находим
Проанализировав выражения, получим, что a> 0, b> 0. Если при этом выполняется равенство a2 = b2, то a = b. Находим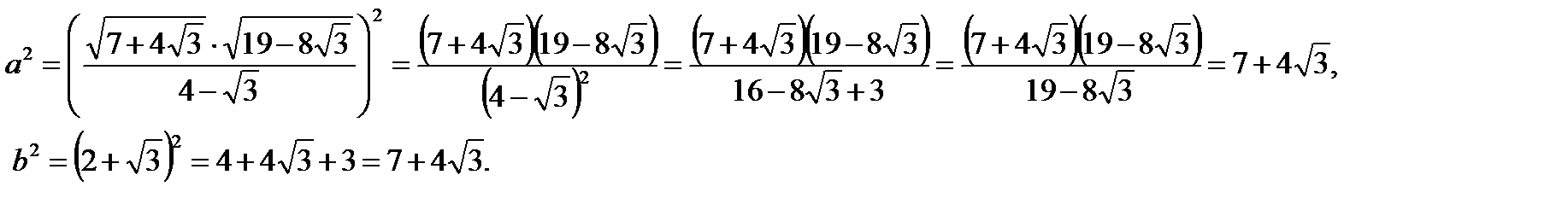
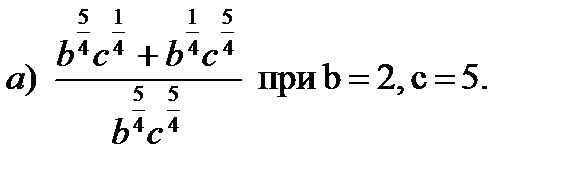
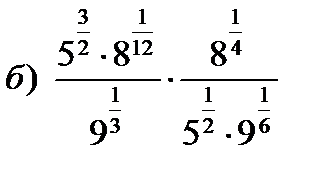 ;
;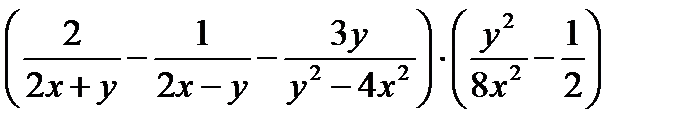
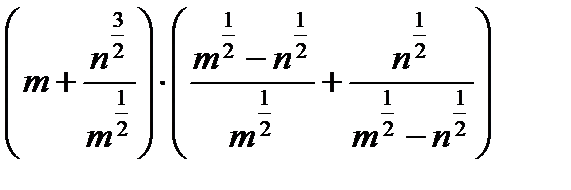
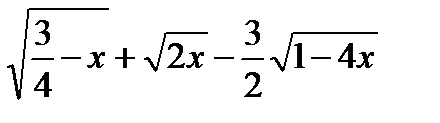 обращается в ноль при
обращается в ноль при 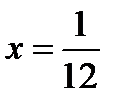 .
.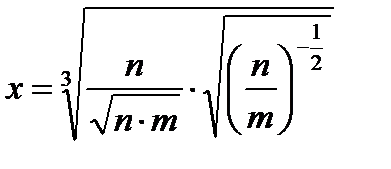 .
.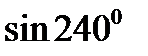 ; б)
; б) 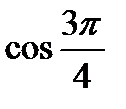
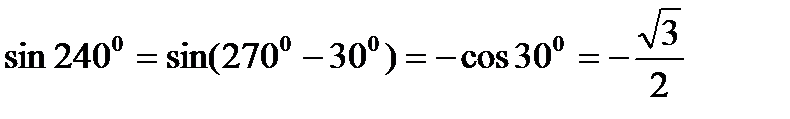
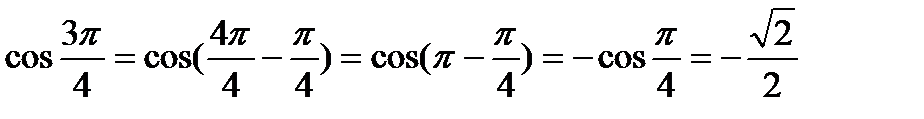
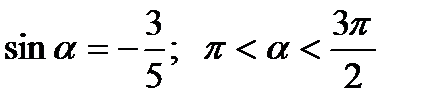
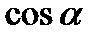 ; б)
; б) 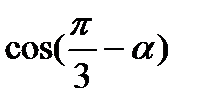
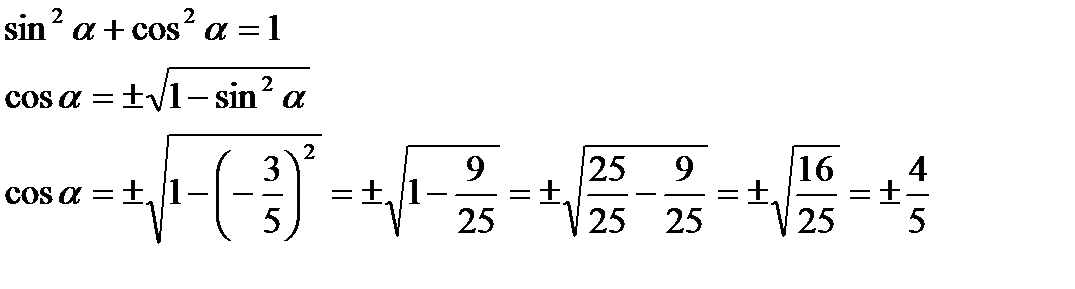
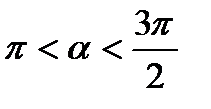 следовательно
следовательно 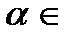 III четверти. Косинус в третьей четверти имеет отрицательный знак. Значит
III четверти. Косинус в третьей четверти имеет отрицательный знак. Значит 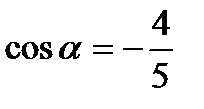 .
.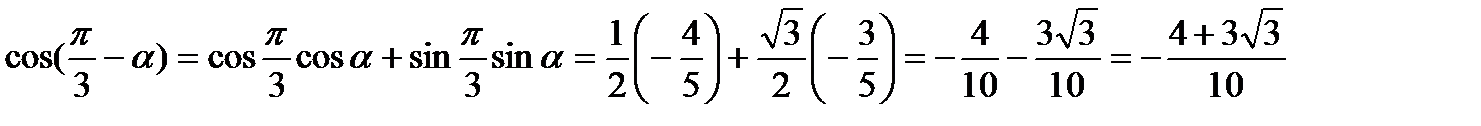 .
.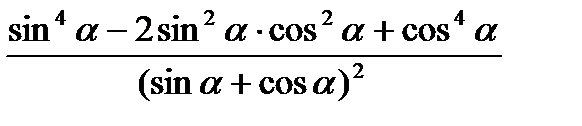
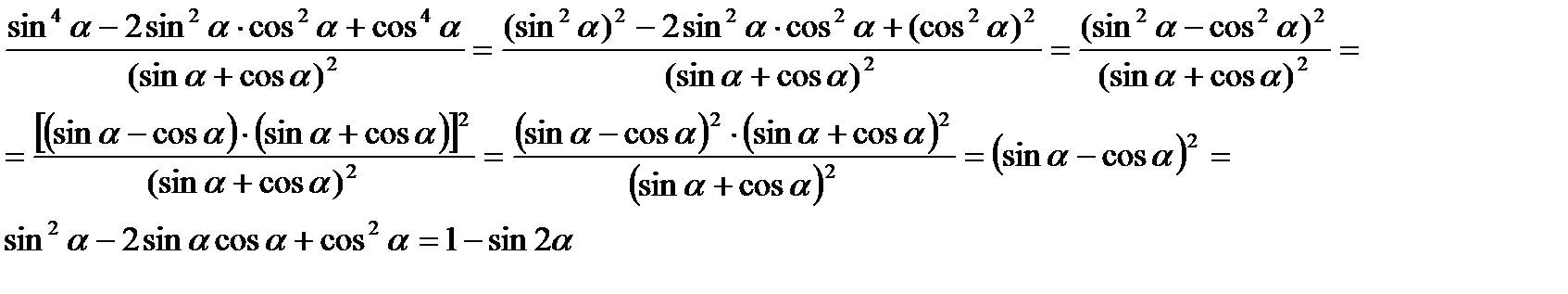
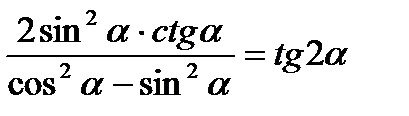
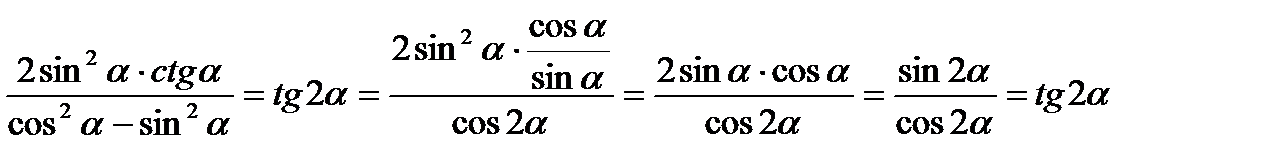
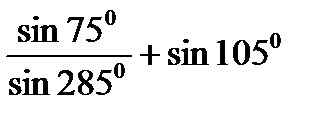 ; б)
; б) 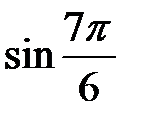
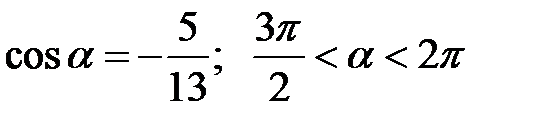
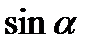 ;
;  б)
б) 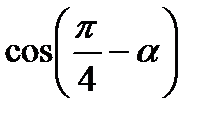
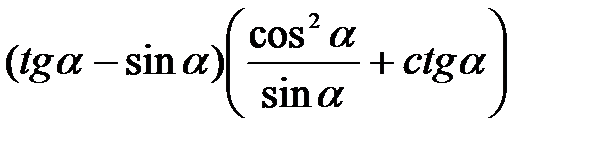
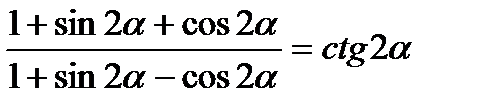 б)
б) 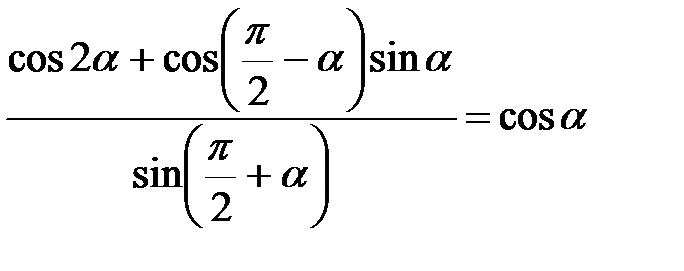
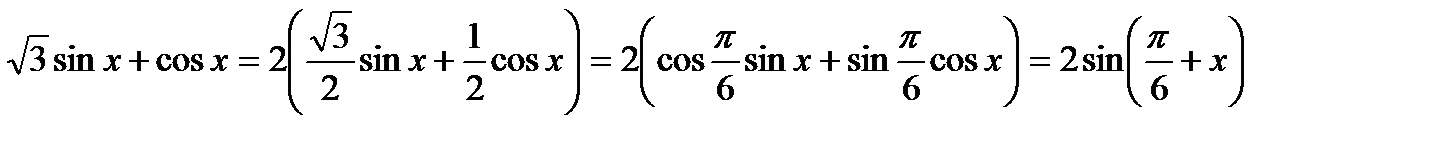
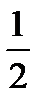 Решение
2x =
Решение
2x = 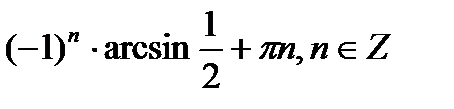 2x =
2x = 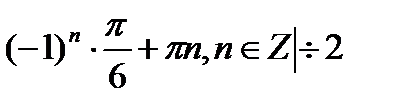 x =
x = 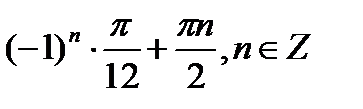
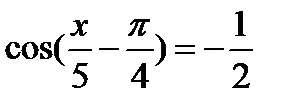 Решение
Решение
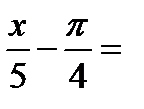
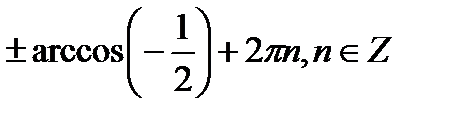
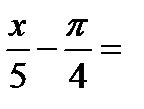
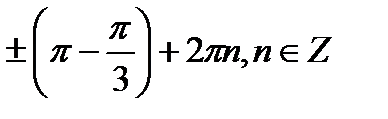
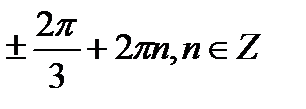
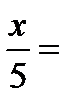
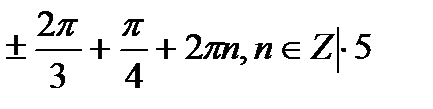
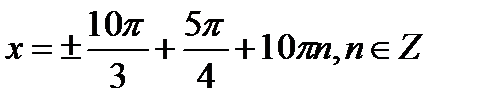
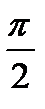 +2πn, n
+2πn, n 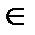 Z.
2) Уравнение sin х = - 6 не имеет решения, так как
Z.
2) Уравнение sin х = - 6 не имеет решения, так как 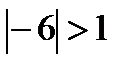 .
.
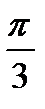 + 2π n, n
+ 2π n, n 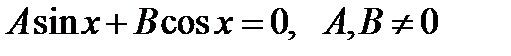 . Разделив обе части уравнения на cosx≠0, получим уравнение вида
. Разделив обе части уравнения на cosx≠0, получим уравнение вида 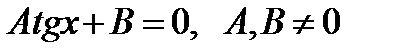 равносильное данному.
равносильное данному.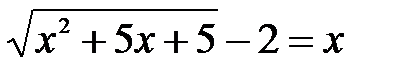

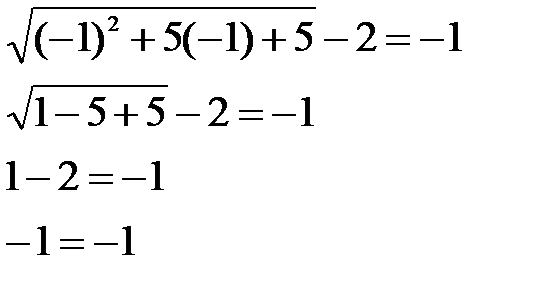
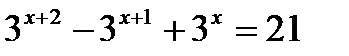
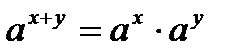 , преобразуем уравнение,
, преобразуем уравнение,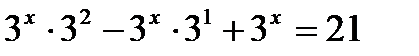
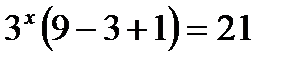
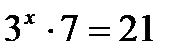
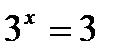
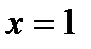

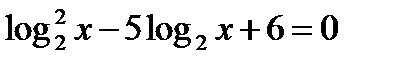
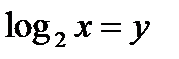 , получаем уравнение
, получаем уравнение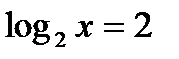 и
и