
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Название практической работыСодержание книги
Поиск на нашем сайте
«Решение тригонометрических уравнений» Цель занятия: Обобщить и систематизировать знания по теме «Тригонометрические уравнения», проверить умение пользоваться различными методами для решения конкретных задач. Контрольные вопросы. 1. Определение обратных тригонометрических функций. 2. Решение простейших тригонометрических уравнений. 3. Решение тригонометрических уравнений методом введения новой переменной. 1. Понятие однородного уравнения и алгоритм решения однородных уравнений. 2. Алгоритм решения тригонометрических уравнений с помощью формул понижения степени. 3. Решение тригонометрических уравнений методом группировки и разложения на множители. 4. Решение тригонометрических уравнений методом преобразования сумм в произведение и произведения в суммы. Примеры и последовательность выполнения заданий. Рекомендации по решению тригонометрических уравнений. 1. Если аргументы функций одинаковые, попробовать получить одинаковые функции, использовав формулы без изменения аргументов. 2. Если аргументы функций отличаются в два раза, попробовать получить одинаковые аргументы, использовав формулы двойного аргумента. 3. Если аргументы функций отличаются в четыре раза, попробовать их привести к промежуточному двойному аргументу. 4. Если в уравнении есть числовое слагаемое (множитель), то его можно представить в виде значений функции угла. Например:
Примеры и последовательность выполнения заданий. Пример 1. Решить простейшее тригонометрическое уравнение. Используя блок-схему для решения тригонометрических уравнений, получим
Пример 2. Тригонометрические уравнения, приводимые к квадратным: A sin2 х + В sin х + С =0 или A sin2 х + В cos х + С =0
Пример 3. а) Однородное тригонометрическое уравнение первого порядка б) Однородное тригонометрическое уравнение второго порядка А sin2 х + В sinх cos х + С cos2х = 0. Разделив обе части уравнения на cos2 x ≠ 0, получим уравнение вида А tg 2x + В tg x + С = 0. Выполнить следующие задания
|
||||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 129; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.237.140 (0.008 с.) |

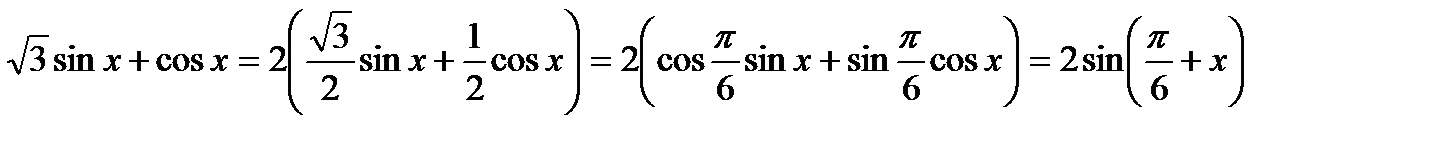
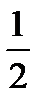 Решение
2x =
Решение
2x = 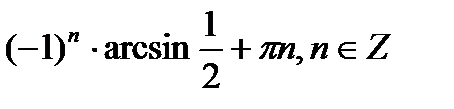 2x =
2x = 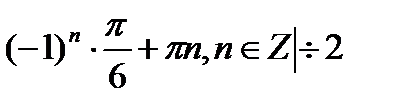 x =
x = 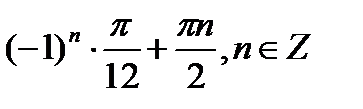
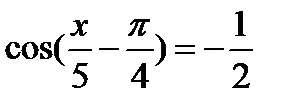 Решение
Решение
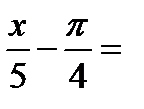
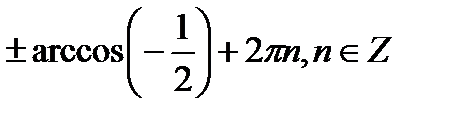
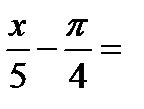
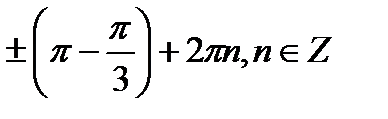
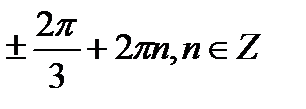
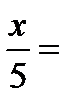
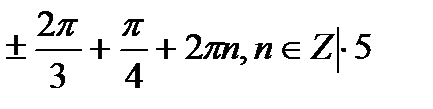
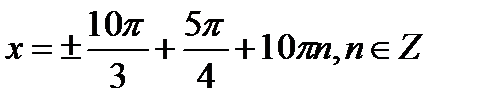
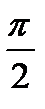 +2πn, n
+2πn, n 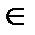 Z.
2) Уравнение sin х = - 6 не имеет решения, так как
Z.
2) Уравнение sin х = - 6 не имеет решения, так как 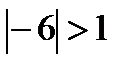 .
.
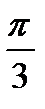 + 2π n, n
+ 2π n, n 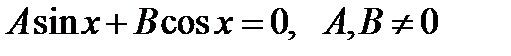 . Разделив обе части уравнения на cosx≠0, получим уравнение вида
. Разделив обе части уравнения на cosx≠0, получим уравнение вида 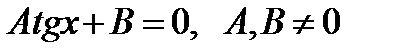 равносильное данному.
равносильное данному.


