
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос № 25. Дайте определение мгновенного центра ускорений. Как определяется его положение. Как оп-ределяются ускорения точек плоской фигуры с помощью мгновенного центра ускорений.
При непоступательном движении плоской фигуры в ее плоскости на фигуре (или на связанной с ней подвижной плоскости) в каждый момент времени имеется точка Q, ускорение которой равно нулю. Эта точка называется мгновенным центром ускорений.
определяется следующим образом (рис. 2.41) 1) находим значение угла M из формулы
3) на полученной полупрямой AN отложим отрезок Конец Q этого отрезка и будет мгновенным центром ускорения. В самом деле, примем точку А за полюс, тогда по формуле распределения ускорений Подставляя сюда значение AQ из равенства (2), находим, что aQA = аА, т.е. модуль вращательного ускорения aQA точки Q вокруг полюса А равен модулю ускорения аА этого полюса. С другой стороны, как было показано в предыдущем параграфе, угол между ускорением точки относительно полюса и направлением на полюс не зависит от выбора полюса. Следовательно, aQA составляет с направлением QA угол µ. Такой же угол составляет и вектор аА с отрезком AQ. Поэтому векторы аА и aQA параллельны, но противоположно направлены. Кроме того, aQA = - аА, а тогда аQ = 0. Таким образом, мы доказали, что точка Q - мгновенный центр ускорений. Если точку Q выбрать за полюс, то, поскольку aQ = 0, ускорение любой точки М плоской фигуры, согласно формуле (3), будет равно ускорению точки М во вращательном движении этой точки вокруг мгновенного центра ускорений, т.е. aM = aMQ.
(5)
т.е. ускорения точек плоской фигуры пропорциональны расстояниям от них до мгновенного центра ускорений. Поле ускорений точек плоской фигуры показано на рис. 2.42. Следует иметь в виду, что при движении плоской фигуры положение ее мгновенного центра ускорений непрерывно меняется, и положение мгновенного центра скоростей Р и мгновенного центра ускорений Q в данный момент времени не совпадают. Например, при качении без скольжения колеса по прямолинейному рельсу, когда скорость центра колеса постоянна, мгновенный центр ускорений в каждый момент времени совпадает с центром колеса, тогда как мгновенный центр скоростей Р находится в точке касания колеса с рельсом. Мгновенные центры скоростей и ускорений совпадают лишь тогда, когда тело вращается вокруг неподвижной оси.
Вопрос № 26. Докажите формулу для определения скоростей точек тела, движущегося около неподвижной точки. Движение твердого тела, имеющего одну неподвижную точку, называют сферическим движением, так как все точки тела движутся по поверхностям сфер, общий центр которых совпадает с неподвижной точкой. Рассмотрим сначала вопрос о задании уравнения, или закона движения тела вокруг неподвижной точки. Предположим, что с телом неизменно связана система координат Oxyz с началом в неподвижной точке О. Положение этой системы будем определять относительно неподвижной системы координат Ox1y1z1 с началом в этой же точке О. В теоретической механике положение подвижной системы координат относительно неподвижной, как правило, определяется при помощи углов Эйлера, которые вводятся следующим образом (рис. 2.47).
Угол между неподвижной осью Ох1 и линией узлов ОК обозначают через ᴪ и называют углом прецессии. Угол между линией узлов OK и подвижной осью Ох обозначают через ф и называют углом собственного вращения. Угол между плоскостями Ох1у1 и Оху, или угол между неподвижной осью Oz1 и подвижной осью Oz, обозначают через ᶿ и называют углом нутации.
Посредством трех последовательных независимых поворотов тела: на угол ᴪ вокруг оси Oz1, затем на угол ᶿ вокруг оси ОК и, наконец, на угол ф вокруг оси Oz - можно подвижную систему координат Oxyz, первоначально совмещенную с неподвижной, перевести в положение, указанное на рис. 2.47. Таким образом, положение тела по отношению к осям Ох1у1 полностью определяется тремя независимыми углами Эйлера, т.е. тело, совершающее сферическое движение, имеет три степени свободы. Если твердое тело совершает движение вокруг неподвижной точки, то углы Эйлера непрерывно изменяются, т.е. являются функциями времени: ᴪ = ᴪ(t), ᶿ = ᶿ (t), ф = Ф(t) (1) Эти уравнения называются уравнениями движения твердого тела вокруг неподвижной точки, или законом его движения.
Вопрос № 27
|
||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 114; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.245.196 (0.007 с.) |
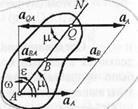 Положение мгновенного центра ускорений в общем случае может быть определено, если известно ускорение какой-либо точки А плоской фигуры, а также ее угловая скорость и угловое ускорение. Тогда положение мгновенного центра ускорений
Положение мгновенного центра ускорений в общем случае может быть определено, если известно ускорение какой-либо точки А плоской фигуры, а также ее угловая скорость и угловое ускорение. Тогда положение мгновенного центра ускорений

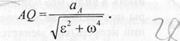 2) из точки А, ускорение которой известно, под углом M к вектору аА проводим полупрямую AN, которая должна быть отклонена от аА на угол M в сторону вращения фигуры, если вращение ускоренное, и против вращения, если оно является замедленным, т.е. в сторону направления углового ускорения E, показанного на рис. 2.41 дуговой стрелкой;
2) из точки А, ускорение которой известно, под углом M к вектору аА проводим полупрямую AN, которая должна быть отклонена от аА на угол M в сторону вращения фигуры, если вращение ускоренное, и против вращения, если оно является замедленным, т.е. в сторону направления углового ускорения E, показанного на рис. 2.41 дуговой стрелкой;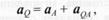
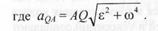
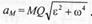 В этом случае модуль ускорения точки М будет
В этом случае модуль ускорения точки М будет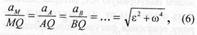 Следовательно, ускорения точек плоской фигуры определяются в данный момент времени так, как если бы движение было вращением вокруг мгновенного центра ускорений. При этом выполняются следующие соотношения:
Следовательно, ускорения точек плоской фигуры определяются в данный момент времени так, как если бы движение было вращением вокруг мгновенного центра ускорений. При этом выполняются следующие соотношения: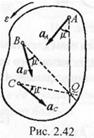
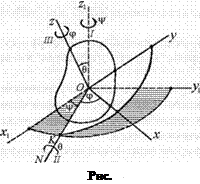 Рассмотрим прямую ОК пересечения плоскостей Ох1y1 и Оху. Эта прямая называется линией узлов. Выберем на линии узлов положительное направление так, чтобы кратчайший переход от оси Oz1 к оси Oz определялся бы в положительном направлении (т.е. против хода часовой стрелки), если смотреть с положительного направления линии узлов.
Рассмотрим прямую ОК пересечения плоскостей Ох1y1 и Оху. Эта прямая называется линией узлов. Выберем на линии узлов положительное направление так, чтобы кратчайший переход от оси Oz1 к оси Oz определялся бы в положительном направлении (т.е. против хода часовой стрелки), если смотреть с положительного направления линии узлов.


