Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дайте определение каждой из осей естественного координатного трехгранника и радиуса кривизны траектории в данной точкеСодержание книги
Поиск на нашем сайте
Вопрос № 2 Вывести формулу для определения скорости точки при векторном способе задания её движения Пусть в некоторый момент времени t положение точки М определяется радиус-вектором r(t), а в момент вектором промежуток времени
Для того, чтобы точно вычислить скорость точки в данный момент времени, необходимо в формуле (1) перейти к пределу при стремлении промежутка времени
Этот предел представляет собой первую векторную производную по времени от радиус-вектора точки по времени. Следовательно, скорость точки в данный момент времени есть векторная величина, равная первой производной от радиус-вектора точки по времени
Как следует из формул (2) и (3), вектор скорости направлен по касательной к траектории точки в сторону ее движения.
Вопрос №3 Вывести формулы определения скорости точки при координатном способе задания её движения Рассмотрим движение точки относительно прямоугольной системы координат (рис. 2.5). В этом случае координаты точки заданы как функции времени:
Разложим радиус-вектор r по ортам декартовой системы координат:
(3) С другой стороны, разложение вектора скорости V по ортам i,j, k можно представить так: (4) где Vх., Vх, Vx –проекции вектора скорости V на оси координат. Сравнивая формулы (3) и (4), находим
Таким образом, проекции скорости на неподвижные декартовы оси координат равны первым производным по времени от соответствующих координат движущейся точки. Из равенства (5) следует, что проекции скорости точки на координатные оси равны скорости проекции этой точки те же оси. Зная проекции вектора скорости точки V, найдем его модуль:
Для определения направления вектора скорости воспользуемся направляющими косинусами:
Вопрос № 4 Вывести формулу для определения скорости точки при естественном способе задания её движения Определим скорость точки, предполагая, что ее движение задано естественным способом. Поэтому будем полагать, что известны траектория движения и закон движения точки по траектории s = s(t) (рис. 2.6). Каждой точке траектории соответствует определенный радиус-вектор r (t) Так как положение каждой точки траектории определяется дуговой координатой S, то радиус-вектор r можно рассматривать как сложную функцию времени t. Тогда
Известно, что так как направлен (при дел. S-»0) совпадает с касательной к траектории в точке М, то вектор единичный вектор касательной к траектории (ее орт), направленный в сторону возрастания криволинейной координаты s. Обозначая орт касательной Т°, запишем формулу (2) в виде (3) Эта формула определяет
т.е. проекция вектора скорости точки на направление касательной к траектории равна первой производной по времени от криволинейной координаты s пo времени. Тогда формулу (3) можно записать так:
Из формулы(5) следует что модуль скорости V=|Vt|. Если Vt > 0, то точка движется в положительном направлении отсчета расстояний и VT=V Если же Vт < 0, точка движется в отрицательном направлении и Vт = — V. Таким образом, модуль вектора скорости IVI (или V) точки равен модулю ее проекции на направление касательной
В качестве примера применения формулы (6) рассмотрим скорость точки М при ее движении по окружности радиуса R (рис. 2.7). Скорость точки М в случае ее движения в положительном направлении отсчета расстояний будет иметь численное значение
так как называется угловой скоростью вращения радиуса ОМ = R. Таким образом, при движении по окружности Направлена скорость по касательной к окружности, следовательно, перпендикулярно радиусу ОМ.
Вопрос № 5 Вывести формулу для определения ускорения точки при векторном способе задания её движения Ускорение - физическая величина, характеризующая быстроту изменения скорости точки во времени. Пусть точка в момент времени t находится в положении М и имеет скорость V (t), а в момент t1= t + дл.t приходит в положение М1 и имеет скорость V1 (рис. 2.8). Тогда за промежуток времени At = t1— t вектор скорости получает векторное приращение Дл = V1—V, которое определяет изменение вектора скорости и по величине, и по направлению. Для определения приращения скорости дл.V перенесем вектор V1 параллельно своему направле нию в точку М. Далее, соединпе концы векторов V и V1, получим дл.V. Разделив вектор дл.V на соответствующий промежуток времени дл.t, получим вектор
который называется вектором среднего ускорения за промежуток времени t. Вектор среднего ускорения характеризует особенности движения точки тем точнее, чем меньшему промежутку времени он соответствует. Поэтому естественно рассмотреть предел, к которому стремится среднее ускорение, если соответствующий промежуток времени At стремится к нулю. Этот предел называют ускорением точки в данный момент времени:
Таким образом, ускорение точки в данный момент времени, есть векторная величина, равная первой производной от вектора скорости или второй производной от радиус-вектора по времени. Установим теперь положение вектора ускорения а относительно траектории. Отметим, что плоскость треугольника МАВ, образованного векторами V, V1, AV, при At—0) будет поворачиваться вокруг вектора V, т.е. вокруг касательной к траектории в точке М, ив пределе займет определенное предельное положение. Это предельное положение плоскости МАВ называется соприкасающейся плоскостью в точке М траектории. Для плоской кривой эта плоскость есть плоскость самой кривой. Как видно из рис. 2.8, вектор среднего ускорения аср направлен так же, как и AV, т.е. в сторону вогнутости траектории точки, и все время находится в плоскости треугольника МАВ.
Вопрос № 6 Вывести формулы для определения ускорения точки при координатном способе задания её движения Рассмотрим движение точки М относительно неподвижной прямоугольной декартовой системы координат (см. рис. 2.5). В этом случае ее движение задано следующим образом:
Разложим радиус-вектор точки по ортам осей Oxyz: Дифференцируя равенство (2) дважды по времени, получим(3)Или, обозначая Т.е. проекции вектора ускорения на неподвижные оси координат равны первым производным по времени от соответствующих проекций вектора скорости или вторым производным от соответствующих координат точки. По этим проекциям определяем величину и направление вектора ускорения:(8) Вопрос № 7 Вопрос № 10 Вопрос № 11 Вопрос № 12 Дайте определение вращательного движение твердого тела вокруг неподвижной оси. Как задается это движение. Докажите формулы угловой скорости и углового ускорения тела. Как связана угловая скорость и число оборотов в минуту Вращательным движением твердого тела называется такое движение, при котором все точки тела описывают концентрические окружности, центры которых лежат на одной прямой, называемой осью вращения. Рассмотрим вопрос о задании уравнения, или закона вращательного движения. Пусть ось Oz является неподвижной осью, вокруг которой вращается тело. Проведем через ось Oz две плоскости: подвижную Р и неподвижную Q (рис. 2.20). Положение вращающегося тела может быть определено двугранным углом ф между этими плоскостями. Назовем угол ф углом поворота тела и условимся считать положительным, если, глядя с положительного конца оси z, угол ф виден отложенным от неподвижной плоскости против хода часовой стрелки. Угол поворота тела обычно измеряют в радианах. Иногда в практических задачах этот угол выражают числом оборотов N тела. Так как один оборот тела соответствует 2П радиан, то получаем зависимость
в положительном направлении отсчета угла поворота ф, т. е. против движения часовой стрелки.Размерность угловой скорости Вопрос № 14, 15 Вывести формулу для определения скорости точек тела, вращающегося вокруг неподвижной оси. Пусть вращение тела вокруг неподвижной оси задано уравнением
(3) или
Так как угловая скорость со является кинематической характеристикой всего тела в целом, то из формулы (5) следует, что скорости точек тела пропорциональны расстояниям этих точек до оси вращения. Ускорение точки М находим, определив сначала касательное Тогда модуль полного ускорения точки М Угол, образованный вектором ускорения точки М с радиусом описываемой точкой окружности, определяется так:
Из формулы (8) следует, что ускорения точек вращающегося тела образуют в данный момент один и тот же угол а с радиусами описываемых ими окружностей. В частном случае равномерного вращения Е=0, поэтому А=0 и, следовательно, полное ускорение по модулю равно нормальному и направлено к оси вращения.
Вопрос № 16, 17 Вывести векторную формулу для скорости точек тела, вращающегося вокруг неподвижной оси. Рассмотрим твердое тело, вращающееся вокруг неподвижной оси Oz с угловой скоростью
Здесь следует заметить, что в разложении (1) х, у, z и вектор k постоянны, т.е. не зависят от времени, a i и j зависят от времени, так как вращаются вместе с телом.
Производные от единичных векторов, входящие в формулу (2), есть скорости концов этих векторов. Например, при ф > О вектор скорости конца i направлен параллельно j в положительном направлении оси Оу, а вектор скорости конца j направлен параллельно i в отрицательном направлении оси Ох. Модуль каждой из этих скоростей равен \ф\. Тогда Далее, учитывая, что j =k*x, a -i =k * j, получим
Подставляя формулы (3) в равенство (2) и используя то, что (4) Назовем вектор фк вектором угловой скорости со, тогда
Как видно из равенства (5), вектор угловой скорости тела направлен вдоль оси вращения так, чтобы наблюдатель, смотрящий с его конца, видел вращение тела против хода часовой стрелки. Вектор ф можно расположить в любом месте оси вращения, т.е. ф — скользящий аксиальный вектор. Перепишем теперь формулу (4) с учетом (5), тогда
Вектор скорости любой точки тела, вращающегося вокруг неподвижной оси, равен векторному произведению вектора угловой скорости тела на радиус-вектор этой точки, проведенный из произвольного центра, взятого на оси вращения. Формула (6) называется формулой Эйлера.
Вопрос № 18 Вопрос № 19 Вопрос № 20 Вопрос № 21 Вопрос № 22 Вопрос № 23 Опишите частные случаи определения положения мгновенного центра скоростей 1, Пусть скорости Va и Vb любых двух течек А к В параллельны друг другу и при этом линия АВ не перпендикулярна к VA, а следовательно, и к VA (рис. 2.34). Из теоремы о проекциях скоростей двух точек на прямую, соединяющую эти точки, следует, что
2. Пусть скорости VA и Vb точек А и В параллельны друг другу и эти точки лежат на одном перпендикуляре к данным скоростям. В этом случае при VA не = Vb мгновенный центр скоростей Р определяется построениями, показанными на рис. 2.35, а и б. Справедливость построения следует из пропорции (6) предыдущего параграфа. Е этом случае для нахождения мгновенного центра скоростей Р нужно, кроме направлений, знать еще и модули скоростей Va и Vb. 3. Е практических задачах часто приходится иметь дело со случаем, когда плоская фигура катится без скольжения по некоторой В этом случае скорость точки касания контура плоской фигуры с кривой MN равна нулю, так как точки касания обоих тел при отсутствии скольжения должны иметь одинаковые скорости, а кривая MN неподвижна. Отсюда следует, что точка касания Р является мгновенным центром скоростей плоской фигуры. В качестве примера на рис. 2.37 показано распределение скоростей точек колеса, которое катится без скольжения по неподвижному прямолинейному рельсу.
Вопрос № 24 Докажите формулу распределения ускорений точек плоской фигуры Пусть плоская фигура (S) движется относительно неподвижной системы координат Оху. В этой системе положения полюса А и произвольной точки В определяются соответственно радиус-векторами rА и rB (рис. 2.39). Скорость произвольной точки В можно определить с помощью формулы распределения скоростей
где р =АВ радиус-вектор, проведенный из полюса А в точку В. Дифференцируя равенство (1) по времени, получим
Здесь
Кроме того, согласно формуле дифференцирования вектора, постоянного по модулю (см. формулу (а), п. 2.16),
(4) В результате равенство (2)
Векторы Atba и Anba представляют те касательное и нормальное ускорения, которые имела бы точка В, если бы фигура (S) совершала только вращение вокруг полюса А. Вопрос о направлении этих векторов изучен нами ранее, однако, пользуясь правилом составления векторного произведения, легко убедиться, что Anba имеет направление, совпадающее с вектором SA (от точки к полюсу), а Atba - перпендикулярно ВА. Модули этих векторов определяются так:
Используя обозначения (6), окончательно находим формулу распределения ускорений (8) или (9) где
Угол M., который образует вектор Aba с направлением ВА, определяется из следующего равенства: (12) Этот угол M одинаков Вопрос № 27 Вопрос № 28 Вопрос № 30 Вопрос № 34 Вопрос № 2 Вывести формулу для определения скорости точки при векторном способе задания её движения Пусть в некоторый момент времени t положение точки М определяется радиус-вектором r(t), а в момент вектором промежуток времени
Для того, чтобы точно вычислить скорость точки в данный момент времени, необходимо в формуле (1) перейти к пределу при стремлении промежутка времени
Этот предел представляет собой первую векторную производную по времени от радиус-вектора точки по времени. Следовательно, скорость точки в данный момент времени есть векторная величина, равная первой производной от радиус-вектора точки по времени
Как следует из формул (2) и (3), вектор скорости направлен по касательной к траектории точки в сторону ее движения.
Вопрос №3 Вывести формулы определения скорости точки при координатном способе задания её движения Рассмотрим движение точки относительно прямоугольной системы координат (рис. 2.5). В этом случае координаты точки заданы как функции времени:
Разложим радиус-вектор r по ортам декартовой системы координат:
(3) С другой стороны, разложение вектора скорости V по ортам i,j, k можно представить так: (4) где Vх., Vх, Vx –проекции вектора скорости V на оси координат. Сравнивая формулы (3) и (4), находим
Таким образом, проекции скорости на неподвижные декартовы оси координат равны первым производным по времени от соответствующих координат движущейся точки. Из равенства (5) следует, что проекции скорости точки на координатные оси равны скорости проекции этой точки те же оси. Зная проекции вектора скорости точки V, найдем его модуль:
Для определения направления вектора скорости воспользуемся направляющими косинусами:
Вопрос № 4 Вывести формулу для определения скорости точки при естественном способе задания её движения Определим скорость точки, предполагая, что ее движение задано естественным способом. Поэтому будем полагать, что известны траектория движения и закон движения точки по траектории s = s(t) (рис. 2.6). Каждой точке траектории соответствует определенный радиус-вектор r (t) Так как положение каждой точки траектории определяется дуговой координатой S, то радиус-вектор r можно рассматривать как сложную функцию времени t. Тогда
Известно, что так как направлен (при дел. S-»0) совпадает с касательной к траектории в точке М, то вектор единичный вектор касательной к траектории (ее орт), направленный в сторону возрастания криволинейной координаты s. Обозначая орт касательной Т°, запишем формулу (2) в виде (3) Эта формула определяет
т.е. проекция вектора скорости точки на направление касательной к траектории равна первой производной по времени от криволинейной координаты s пo времени. Тогда формулу (3) можно записать так:
Из формулы(5) следует что модуль скорости V=|Vt|. Если Vt > 0, то точка движется в положительном направлении отсчета расстояний и VT=V Если же Vт < 0, точка движется в отрицательном направлении и Vт = — V. Таким образом, модуль вектора скорости IVI (или V) точки равен модулю ее проекции на направление касательной
В качестве примера применения формулы (6) рассмотрим скорость точки М при ее движении по окружности радиуса R (рис. 2.7). Скорость точки М в случае ее движения в положительном направлении отсчета расстояний будет иметь численное значение
так как называется угловой скоростью вращения радиуса ОМ = R. Таким образом, при движении по окружности Направлена скорость по касательной к окружности, следовательно, перпендикулярно радиусу ОМ.
Вопрос № 5 Вывести формулу для определения ускорения точки при векторном способе задания её движения Ускорение - физическая величина, характеризующая быстроту изменения скорости точки во времени. Пусть точка в момент времени t находится в положении М и имеет скорость V (t), а в момент t1= t + дл.t приходит в положение М1 и имеет скорость V1 (рис. 2.8). Тогда за промежуток времени At = t1— t вектор скорости получает векторное приращение Дл = V1—V, которое определяет изменение вектора скорости и по величине, и по направлению. Для определения приращения скорости дл.V перенесем вектор V1 параллельно своему направле нию в точку М. Далее, соединпе концы векторов V и V1, получим дл.V. Разделив вектор дл.V на соответствующий промежуток времени дл.t, получим вектор
который называется вектором среднего ускорения за промежуток времени t. Вектор среднего ускорения характеризует особенности движения точки тем точнее, чем меньшему промежутку времени он соответствует. Поэтому естественно рассмотреть предел, к которому стремится среднее ускорение, если соответствующий промежуток времени At стремится к нулю. Этот предел называют ускорением точки в данный момент времени:
Таким образом, ускорение точки в данный момент времени, есть векторная величина, равная первой производной от вектора скорости или второй производной от радиус-вектора по времени. Установим теперь положение вектора ускорения а относительно траектории. Отметим, что плоскость треугольника МАВ, образованного векторами V, V1, AV, при At—0) будет поворачиваться вокруг вектора V, т.е. вокруг касательной к траектории в точке М, ив пределе займет определенное предельное положение. Это предельное положение плоскости МАВ называется соприкасающейся плоскостью в точке М траектории. Для плоской кривой эта плоскость есть плоскость самой кривой. Как видно из рис. 2.8, вектор среднего ускорения аср направлен так же, как и AV, т.е. в сторону вогнутости траектории точки, и все время находится в плоскости треугольника МАВ.
Вопрос № 6 Вывести формулы для определения ускорения точки при координатном способе задания её движения Рассмотрим движение точки М относительно неподвижной прямоугольной декартовой системы координат (см. рис. 2.5). В этом случае ее движение задано следующим образом:
Разложим радиус-вектор точки по ортам осей Oxyz: Дифференцируя равенство (2) дважды по времени, получим(3)Или, обозначая Т.е. проекции вектора ускорения на неподвижные оси координат равны первым производным по времени от соответствующих проекций вектора скорости или вторым производным от соответствующих координат точки. По этим проекциям определяем величину и направление вектора ускорения:(8) Вопрос № 7 Дайте определение каждой из осей естественного координатного трехгранника и радиуса кривизны траектории в данной точке Рассмотрим пространственную кривую. Предельное положение секущей, проходящей через точки М и M1 кривой, когда точка M1 стремится к точке М, называется касательной к кривой в данной точке М. Перпендикуляр к касательной в точке М называется нормалью к кривой в этой точке. Геометрическое место нормалей к данной кривой в данной точке называется нормальной плоскостью. Линия пересечения нормальной и соприкасающейся плоскостей называется главной нормалью. Нормаль, перпендикулярная главной нормали, называется бинормалью.
Обозначим единичные векторы: касательной через т°, главной нормали n° и бинормали b°. Через эти векторы проходят плоскости: (т°, n0) - соприкасающаяся, (n0, Ь°) - нормальная и (b°, т°) - спрямляющая. Три взаимно перпендикулярных направления, которые определяются векторами т°, n° и b°, образуют естественную систему координат, или так называемый естественный, или подвижный, трехгранник. Направление т°, n0 и b° определяются так же как направление координатных осей, т.е. по правой системе, при этом единичный вектор главной нормали всегда направлен в сторону вогнутости кривой (рис. 2.9). Проведем теперь в двух точках кривой М и М1 единичные векторы касательных т° и т1°.Угол между этими касательными называется углом смежности. Обозначим этот угол через дл.8, а длину дуги ММ1 через дл,s (рис. 2.10). Предел отношения дл.8 и дл.s при дл.s-*0, т.е. Найдем кривизну окружности радиуса R. Возьмем на окружности дугу АВ = дл.s и проведем в точках А и В касательные к окружности (рис. 2. 11). Тогда(2) Отсюда следует, ч
|
||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 162; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.72.24 (0.016 с.) |

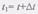 - радиус-
- радиус-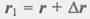 (рис. 2.4). Тогда перемещение точки М за
(рис. 2.4). Тогда перемещение точки М за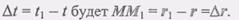
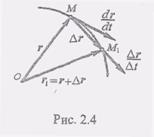 Будем считать, что промежуток времени дел.t настолько мал, что с достаточной степенью точности можно предполагать перемещение точки М в положение М1, происходящим равномерно и прямолинейно. В этом случае скорость точки М можно приближенно вычислить так:
Будем считать, что промежуток времени дел.t настолько мал, что с достаточной степенью точности можно предполагать перемещение точки М в положение М1, происходящим равномерно и прямолинейно. В этом случае скорость точки М можно приближенно вычислить так: (1)
(1) ' к нулю, т.е.
' к нулю, т.е.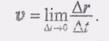 (2)
(2)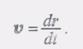 (3)
(3)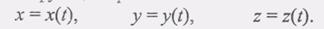 (1)
(1)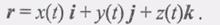 (2)
(2)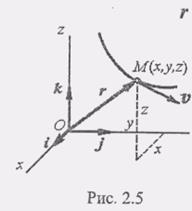 Зная, что вектор скорости V равен первой производной от радиус-вектора, продифференцируем равенство (2) по времени. В результате получим разложение скорости по ортам i,j, к:
Зная, что вектор скорости V равен первой производной от радиус-вектора, продифференцируем равенство (2) по времени. В результате получим разложение скорости по ортам i,j, к: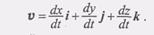
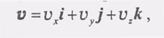
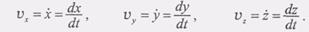 (5)
(5) (6)
(6)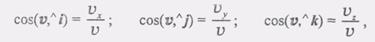 (7) где Vx, Vy, Vz, и V определяются равенствами (5) и (6).
(7) где Vx, Vy, Vz, и V определяются равенствами (5) и (6).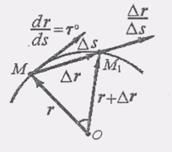
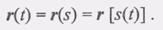 (1) Найдем теперь вектор скорости V точки:
(1) Найдем теперь вектор скорости V точки: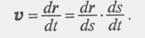 (2)
(2)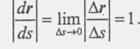 Далее,
Далее, пределе
пределе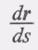 есть
есть 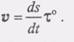 вектор скорости при естественном способе задания движения точки Умножая скалярно обе части равенства (3) на т° и учитывая, что
вектор скорости при естественном способе задания движения точки Умножая скалярно обе части равенства (3) на т° и учитывая, что  получим
получим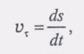 (4)
(4)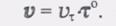 (5)
(5)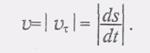 (6)
(6) (7)
(7)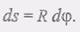 Величина
Величина 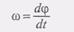 (8)
(8)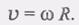 (9)
(9)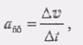 (1)
(1)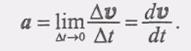 (2)
(2)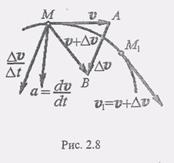 Так как вектор скорости есть первая производная радиус-вектора точки по времени, то
Так как вектор скорости есть первая производная радиус-вектора точки по времени, то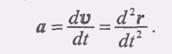 (3)
(3)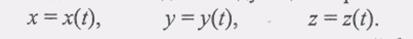 (1)
(1)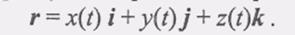 (2)
(2)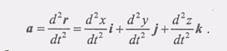 вторые производные по-времени двумя точками, получим разложение ускорения по осям декартовой системы координат в следующем виде:
вторые производные по-времени двумя точками, получим разложение ускорения по осям декартовой системы координат в следующем виде: 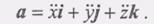 (4) С другой стороны, известно, что
(4) С другой стороны, известно, что 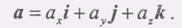 (5)Сравнивая равенства (4) и (5), находим формулы для вычисления проекций ускорения на оси декартовой системы координат:
(5)Сравнивая равенства (4) и (5), находим формулы для вычисления проекций ускорения на оси декартовой системы координат: 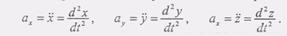 (6)Так как Vx= х, Vy= у, Vz= z, то формулы (6) можно представить еще и так:
(6)Так как Vx= х, Vy= у, Vz= z, то формулы (6) можно представить еще и так: 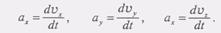 О)
О)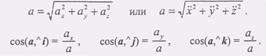 (9)Если во все время движения точка остается в одной плоскости, например в плоскости Оху, то в этом случае во всех формулах нужно положить z = 0.
(9)Если во все время движения точка остается в одной плоскости, например в плоскости Оху, то в этом случае во всех формулах нужно положить z = 0. (1)
(1)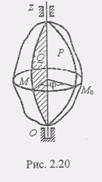 При вращении тела угол поворота изменяется с течением времени, т.е.
При вращении тела угол поворота изменяется с течением времени, т.е. 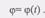 (2)Равенство (2) называется уравнением, или законом вращательного движения твердого тела вокруг неподвижной оси.Рассмотрим теперь основные кинематические величины, характеризующие вращательное движение тела. Этими величинами являются угловая скорость тела омега и угловое ускорение е.Угловой скоростью тела называется физическая величина, характеризующая быстроту изменения угла поворота <р тела во времени, т.е.
(2)Равенство (2) называется уравнением, или законом вращательного движения твердого тела вокруг неподвижной оси.Рассмотрим теперь основные кинематические величины, характеризующие вращательное движение тела. Этими величинами являются угловая скорость тела омега и угловое ускорение е.Угловой скоростью тела называется физическая величина, характеризующая быстроту изменения угла поворота <р тела во времени, т.е. 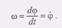 (3)В самом деле, пусть за промежуток времени дл.t; угол поворота ср получил приращение дл.ФИ. Тогда средняя угловая скорость определится равенством
(3)В самом деле, пусть за промежуток времени дл.t; угол поворота ср получил приращение дл.ФИ. Тогда средняя угловая скорость определится равенством  (4)Предел этого отношения при дл.t—>0 называют угловой скоростью тела в данный момент времени
(4)Предел этого отношения при дл.t—>0 называют угловой скоростью тела в данный момент времени 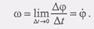 (5)Мы вновь пришли к равенству (3). Итак, угловая скорость тела равна первой производной по времени от угла поворота тела. Значение угловой скорости омега для данного момента времени может быть положительным или отрицательным в зависимости от того, возрастает или убывает угол поворота тела.Если
(5)Мы вновь пришли к равенству (3). Итак, угловая скорость тела равна первой производной по времени от угла поворота тела. Значение угловой скорости омега для данного момента времени может быть положительным или отрицательным в зависимости от того, возрастает или убывает угол поворота тела.Если  то тело в данный момент времени вращается
то тело в данный момент времени вращается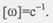 В технике угловую скорость характеризуют числом оборотов в минуту и обозначают буквой п. Замечая, что п об/мин соответствует п/60 об/с и что 1 оборот соответствует 2П радианам, получим:
В технике угловую скорость характеризуют числом оборотов в минуту и обозначают буквой п. Замечая, что п об/мин соответствует п/60 об/с и что 1 оборот соответствует 2П радианам, получим:  (6)Угловым ускорением называется физическая величина, характеризующая быстроту изменения угловой скорости тела во времени:
(6)Угловым ускорением называется физическая величина, характеризующая быстроту изменения угловой скорости тела во времени: 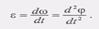 (7)Эту меру быстроты изменения угловой скорости можно получить как предел приращения угловой скорости к приращению времени:
(7)Эту меру быстроты изменения угловой скорости можно получить как предел приращения угловой скорости к приращению времени: 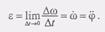 (8)Таким образом, угловое ускорение тела в данный момент времени равно первой производной по времени от угловой скорости или второй производной от угла поворота.Размерность углового ускорения
(8)Таким образом, угловое ускорение тела в данный момент времени равно первой производной по времени от угловой скорости или второй производной от угла поворота.Размерность углового ускорения 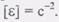 Если знаки угловой скорости и углового ускорения одинаковы, то вращение тела в данный момент ускоренное, если же знаки омега и е различны, вращение замедленное.
Если знаки угловой скорости и углового ускорения одинаковы, то вращение тела в данный момент ускоренное, если же знаки омега и е различны, вращение замедленное.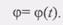 (1) Найдем распределение скоростей точек тела при его вращении. Воспользуемся при этом естественным способом задания движения точки. Рассмотрим движение какой-нибудь точки М тела. При вращении тела точка М будет описывать окружность, радиус которой обозначим R (рис. 2.21).
(1) Найдем распределение скоростей точек тела при его вращении. Воспользуемся при этом естественным способом задания движения точки. Рассмотрим движение какой-нибудь точки М тела. При вращении тела точка М будет описывать окружность, радиус которой обозначим R (рис. 2.21).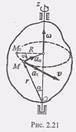 Составим уравнение движения точки М по ее траектории. За начало отсчета примем начальное положение Мо, а за положительное направление дуги s - направление отсчета угла поворота ф. Тогда уравнением движения точки М по ее траектории будет
Составим уравнение движения точки М по ее траектории. За начало отсчета примем начальное положение Мо, а за положительное направление дуги s - направление отсчета угла поворота ф. Тогда уравнением движения точки М по ее траектории будет 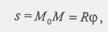 (2) а следовательно, проекция скорости точки М на направление касательной определится следующим образом:
(2) а следовательно, проекция скорости точки М на направление касательной определится следующим образом: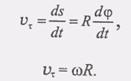 (4) Эту скорость точки М, в отличие от угловой скорости тела, часто называют линейной скоростью. Таким образом, линейная скорость какой-либо точки вращающегося твердого тела равна произведению угловой скорости тела на расстояние от этой точки до оси вращения. Вектор V скорости точки М направлен по касательной к окружности, которую описывает точка М, т.е. перпендикулярен к радиусу этой окружности. Модуль V вектора скорости V равен
(4) Эту скорость точки М, в отличие от угловой скорости тела, часто называют линейной скоростью. Таким образом, линейная скорость какой-либо точки вращающегося твердого тела равна произведению угловой скорости тела на расстояние от этой точки до оси вращения. Вектор V скорости точки М направлен по касательной к окружности, которую описывает точка М, т.е. перпендикулярен к радиусу этой окружности. Модуль V вектора скорости V равен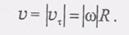 (5)
(5) и нормальное ускорения:
и нормальное ускорения: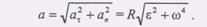 (7)
(7)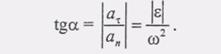 (8)
(8) Определим скорость произвольной точки М этого тела. Введем прямоугольную систему координат с началом на оси вращения и неизменно связанную с телом (рис. 2.22).В этом случае
Определим скорость произвольной точки М этого тела. Введем прямоугольную систему координат с началом на оси вращения и неизменно связанную с телом (рис. 2.22).В этом случае (1)
(1)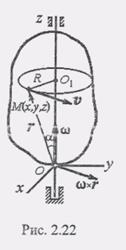 Тогда для скорости точки М имеем(2)
Тогда для скорости точки М имеем(2) 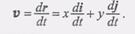
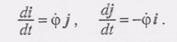
 (3)
(3)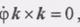 , найдем
, найдем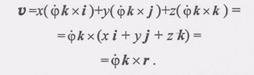
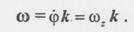 (5)
(5) (6)
(6)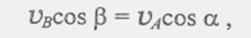 но а = B, поэтому VB = VA и, следовательно, Vb = VA.
но а = B, поэтому VB = VA и, следовательно, Vb = VA.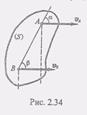 Таким образом, в рассматриваемом случае скорости всех точек плоской фигуры в данный момент равны и по модулю, и по направлению. Такое состояние плоской фигуры называется мгновенно поступательным. Так как перпендикуляры, восстановленные из точек А и В к скоростям этих точек, не пересекаются, то в рассматриваемом случае в данный момент мгновенный центр скоростей находится в бесконечности. Угловая скорость со плоской фигуры в этот момент равна нулю.
Таким образом, в рассматриваемом случае скорости всех точек плоской фигуры в данный момент равны и по модулю, и по направлению. Такое состояние плоской фигуры называется мгновенно поступательным. Так как перпендикуляры, восстановленные из точек А и В к скоростям этих точек, не пересекаются, то в рассматриваемом случае в данный момент мгновенный центр скоростей находится в бесконечности. Угловая скорость со плоской фигуры в этот момент равна нулю.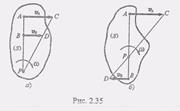
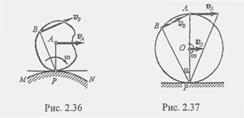 неподвижной кривой MN (рис. 2.36).
неподвижной кривой MN (рис. 2.36).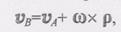 (1)
(1)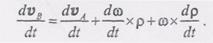 (2)
(2)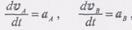 , т.е. соответственно равны ускорениям полюса А и точки В. Производная
, т.е. соответственно равны ускорениям полюса А и точки В. Производная 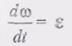 есть вектор углового ускорения фигуры,направленный (как и (О) перпендикулярно к плоскости фигуры.
есть вектор углового ускорения фигуры,направленный (как и (О) перпендикулярно к плоскости фигуры.
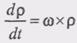 . Тогда последнее слагаемое формулы (2), раскрыв двойное векторное произведение, можно представить так
. Тогда последнее слагаемое формулы (2), раскрыв двойное векторное произведение, можно представить так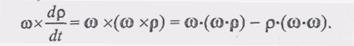 (3)
(3)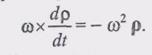 окончательно можно записать так:
окончательно можно записать так: (5) Введем обозначения:
(5) Введем обозначения: (6)
(6) (7)
(7)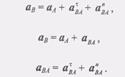 (10)Таким образом, ускорение любой точки В плоской фигуры в каждый данный момент равно геометрической сумме двух ускорений: ускорения произвольного полюса А и ускорения точки В в ее вращательном движении вместе с плоской фигурой вокруг этого полюса.Так как модуль ускорения точки В при вращении фигуры вокруг
(10)Таким образом, ускорение любой точки В плоской фигуры в каждый данный момент равно геометрической сумме двух ускорений: ускорения произвольного полюса А и ускорения точки В в ее вращательном движении вместе с плоской фигурой вокруг этого полюса.Так как модуль ускорения точки В при вращении фигуры вокруг 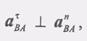 полюса А находится так:
полюса А находится так: 
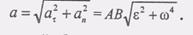 (И)
(И)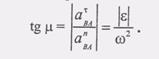 для всех точек плоской фигуры. Полученные результаты позволяют построить вектор Ab так, как это показано на рис. 2.40.
для всех точек плоской фигуры. Полученные результаты позволяют построить вектор Ab так, как это показано на рис. 2.40.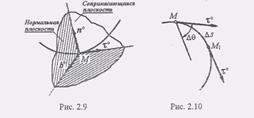
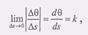 (1)называется кривизной кривой в данной точке М.
(1)называется кривизной кривой в данной точке М.