
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сформулируйте и докажите теорему о проекциях скоростей двух точек плоской фигуры на прямую, соединяющую эти точки
Определение скоростей точек тела с помощью доказанной формулы распределения скоростей часто связано с достаточно сложными расчетами. Однако, используя упомянутую формулу, можно получить другие более удобные и простые методы определения скоростей точек плоской фигуры (рис. 2.31).
Рассмотрим какие-нибудь две точки А я В, движущиеся в своей плоскости плоской фигуры (S). Предположим, что известны модуль и направление скорости точки А и направление скорости точки В. Принимая точку А за полюс, можно записать, что (1) Проецируя обе части этогоравенства на линию АВ и учитывая, что вектор Vba перпендикулярен к АВ, приходим к результату
Доказанная теорема* позволяет находить модуль скорости Vb точки В, если известны модуль и направление скорости Va точки А и направление скорости Vb точки В.
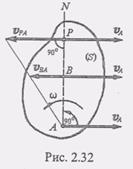
Вопрос № 22 Опишите, как определяются скорости точек плоской фигуры и её угловая скорость с помощью мгновенного центра скоростей Другой простой и наглядный способ определения скоростей точек тела при плоскопараллельном движении основан па понятии о мгновенном центре скоростей. Формула распределения скоростей, полученная ранее, основывалась на представлении о перемещении плоской фигуры в виде геометрической суммы поступательного перемещения полюса и вращательного перемещения вокруг полюса (теорема 1). Упрощение картины распределения скоростей можно получить, основываясь на представлении перемещения плоской фигуры по теореме Эйлера - Шаля (теорема 2). Докажем теорему. При всяком непоступательном перемещении плоской фигуры существует единственная точка этой фигуры, скорость которой в данный момент равна нулю. Точка Р плоской фигуры, скорость которой в данный момент времени равна нулю, называется мгновенным центром скоростей. Для доказательства восстановим из точки А плоской фигуры перпендикуляр AN к направлению скорости Va так, чтобы угол 90 между Va и линией AN был отсчитан в сторону вращения плоской фигуры (рис. 2.32). Тогда, по доказанной ранее формуле, вектор скорости любой точки В, лежащей на перпендикуляре AN,
а величина скорости Vb в силу того, что Va и Vb лежат на одной прямой, будет
Изменяя расстояние точки В от точки А, можно найти при ф не = 0 такую точку Р, чтобы VPA = -VA, тогда (3) при этом
Таким образом, теорема доказана.
Вопрос № 23 Опишите частные случаи определения положения мгновенного центра скоростей 1, Пусть скорости Va и Vb любых двух течек А к В параллельны друг другу и при этом линия АВ не перпендикулярна к VA, а следовательно, и к VA (рис. 2.34). Из теоремы о проекциях скоростей двух точек на прямую, соединяющую эти точки, следует, что
2. Пусть скорости VA и Vb точек А и В параллельны друг другу и эти точки лежат на одном перпендикуляре к данным скоростям. В этом случае при VA не = Vb мгновенный центр скоростей Р определяется построениями, показанными на рис. 2.35, а и б. Справедливость построения следует из пропорции (6) предыдущего параграфа. Е этом случае для нахождения мгновенного центра скоростей Р нужно, кроме направлений, знать еще и модули скоростей Va и Vb. 3. Е практических задачах часто приходится иметь дело со случаем, когда плоская фигура катится без скольжения по некоторой В этом случае скорость точки касания контура плоской фигуры с кривой MN равна нулю, так как точки касания обоих тел при отсутствии скольжения должны иметь одинаковые скорости, а кривая MN неподвижна. Отсюда следует, что точка касания Р является мгновенным центром скоростей плоской фигуры. В качестве примера на рис. 2.37 показано распределение скоростей точек колеса, которое катится без скольжения по неподвижному прямолинейному рельсу.
Вопрос № 24 Докажите формулу распределения ускорений точек плоской фигуры Пусть плоская фигура (S) движется относительно неподвижной системы координат Оху. В этой системе положения полюса А и произвольной точки В определяются соответственно радиус-векторами rА и rB (рис. 2.39). Скорость произвольной точки В можно определить с помощью формулы распределения скоростей
где р =АВ радиус-вектор, проведенный из полюса А в точку В. Дифференцируя равенство (1) по времени, получим
Здесь
Кроме того, согласно формуле дифференцирования вектора, постоянного по модулю (см. формулу (а), п. 2.16),
(4) В результате равенство (2)
Векторы Atba и Anba представляют те касательное и нормальное ускорения, которые имела бы точка В, если бы фигура (S) совершала только вращение вокруг полюса А. Вопрос о направлении этих векторов изучен нами ранее, однако, пользуясь правилом составления векторного произведения, легко убедиться, что Anba имеет направление, совпадающее с вектором SA (от точки к полюсу), а Atba - перпендикулярно ВА. Модули этих векторов определяются так:
Используя обозначения (6), окончательно находим формулу распределения ускорений (8) или (9) где
Угол M., который образует вектор Aba с направлением ВА, определяется из следующего равенства: (12) Этот угол M одинаков
|
||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 132; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.174.168 (0.008 с.) |
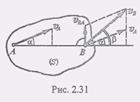 Один из таких методов дает теорема: проекции скоростей двух точек плоской фигуры на прямую, соединяющие эти точки, равны между собой.
Один из таких методов дает теорема: проекции скоростей двух точек плоской фигуры на прямую, соединяющие эти точки, равны между собой.
 (2)
(2)
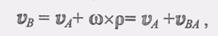 (1)
(1)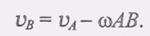 (2)
(2)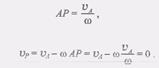 (4)
(4)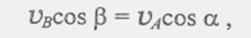 но а = B, поэтому VB = VA и, следовательно, Vb = VA.
но а = B, поэтому VB = VA и, следовательно, Vb = VA.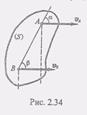 Таким образом, в рассматриваемом случае скорости всех точек плоской фигуры в данный момент равны и по модулю, и по направлению. Такое состояние плоской фигуры называется мгновенно поступательным. Так как перпендикуляры, восстановленные из точек А и В к скоростям этих точек, не пересекаются, то в рассматриваемом случае в данный момент мгновенный центр скоростей находится в бесконечности. Угловая скорость со плоской фигуры в этот момент равна нулю.
Таким образом, в рассматриваемом случае скорости всех точек плоской фигуры в данный момент равны и по модулю, и по направлению. Такое состояние плоской фигуры называется мгновенно поступательным. Так как перпендикуляры, восстановленные из точек А и В к скоростям этих точек, не пересекаются, то в рассматриваемом случае в данный момент мгновенный центр скоростей находится в бесконечности. Угловая скорость со плоской фигуры в этот момент равна нулю.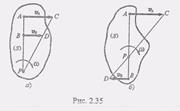
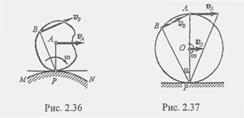 неподвижной кривой MN (рис. 2.36).
неподвижной кривой MN (рис. 2.36).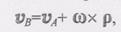 (1)
(1)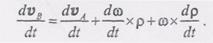 (2)
(2)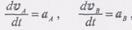 , т.е. соответственно равны ускорениям полюса А и точки В. Производная
, т.е. соответственно равны ускорениям полюса А и точки В. Производная 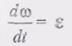 есть вектор углового ускорения фигуры,направленный (как и (О) перпендикулярно к плоскости фигуры.
есть вектор углового ускорения фигуры,направленный (как и (О) перпендикулярно к плоскости фигуры.
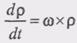 . Тогда последнее слагаемое формулы (2), раскрыв двойное векторное произведение, можно представить так
. Тогда последнее слагаемое формулы (2), раскрыв двойное векторное произведение, можно представить так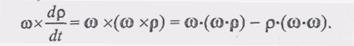 (3)
(3)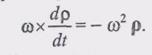 окончательно можно записать так:
окончательно можно записать так: (5) Введем обозначения:
(5) Введем обозначения: (6)
(6) (7)
(7)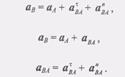 (10)Таким образом, ускорение любой точки В плоской фигуры в каждый данный момент равно геометрической сумме двух ускорений: ускорения произвольного полюса А и ускорения точки В в ее вращательном движении вместе с плоской фигурой вокруг этого полюса.Так как модуль ускорения точки В при вращении фигуры вокруг
(10)Таким образом, ускорение любой точки В плоской фигуры в каждый данный момент равно геометрической сумме двух ускорений: ускорения произвольного полюса А и ускорения точки В в ее вращательном движении вместе с плоской фигурой вокруг этого полюса.Так как модуль ускорения точки В при вращении фигуры вокруг 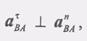 полюса А находится так:
полюса А находится так: 
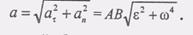 (И)
(И)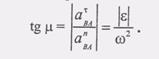 для всех точек плоской фигуры. Полученные результаты позволяют построить вектор Ab так, как это показано на рис. 2.40.
для всех точек плоской фигуры. Полученные результаты позволяют построить вектор Ab так, как это показано на рис. 2.40.


