
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос № 13Вывести формулы равномерного и равнопеременного вращательного движения твердого тела. Начертите график равнопеременного вращательного движения
Вращение тела называют равномерным, если угловая скорость тела постоянна, т.е. (1) Равенство (2) называется законом равномерного вращательного движения твердого тела. При Равнопеременным вращением называется такое вращательное движение тела, при котором его угловое ускорение постоянно, т.е. Из начального условия Равенство (6) называется законом равнопеременного вращательного движения твердого тела. Легко заметить аналогию между полученными формулами (2) и (6) и формулами равномерного и равнопеременного движения точки. Соответствующие формулы совпадают с точностью до обозначений. Вопрос № 14, 15 Вывести формулу для определения скорости точек тела, вращающегося вокруг неподвижной оси. Пусть вращение тела вокруг неподвижной оси задано уравнением
(3) или
Так как угловая скорость со является кинематической характеристикой всего тела в целом, то из формулы (5) следует, что скорости точек тела пропорциональны расстояниям этих точек до оси вращения. Ускорение точки М находим, определив сначала касательное Тогда модуль полного ускорения точки М Угол, образованный вектором ускорения точки М с радиусом описываемой точкой окружности, определяется так:
Из формулы (8) следует, что ускорения точек вращающегося тела образуют в данный момент один и тот же угол а с радиусами описываемых ими окружностей. В частном случае равномерного вращения Е=0, поэтому А=0 и, следовательно, полное ускорение по модулю равно нормальному и направлено к оси вращения.
Вопрос № 16, 17 Вывести векторную формулу для скорости точек тела, вращающегося вокруг неподвижной оси. Рассмотрим твердое тело, вращающееся вокруг неподвижной оси Oz с угловой скоростью
Здесь следует заметить, что в разложении (1) х, у, z и вектор k постоянны, т.е. не зависят от времени, a i и j зависят от времени, так как вращаются вместе с телом.
Производные от единичных векторов, входящие в формулу (2), есть скорости концов этих векторов. Например, при ф > О вектор скорости конца i направлен параллельно j в положительном направлении оси Оу, а вектор скорости конца j направлен параллельно i в отрицательном направлении оси Ох. Модуль каждой из этих скоростей равен \ф\. Тогда Далее, учитывая, что j =k*x, a -i =k * j, получим
Подставляя формулы (3) в равенство (2) и используя то, что (4) Назовем вектор фк вектором угловой скорости со, тогда
Как видно из равенства (5), вектор угловой скорости тела направлен вдоль оси вращения так, чтобы наблюдатель, смотрящий с его конца, видел вращение тела против хода часовой стрелки.
Вектор ф можно расположить в любом месте оси вращения, т.е. ф — скользящий аксиальный вектор. Перепишем теперь формулу (4) с учетом (5), тогда
Вектор скорости любой точки тела, вращающегося вокруг неподвижной оси, равен векторному произведению вектора угловой скорости тела на радиус-вектор этой точки, проведенный из произвольного центра, взятого на оси вращения. Формула (6) называется формулой Эйлера.
Вопрос № 18
|
||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 212; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.201.209 (0.007 с.) |
 В этом случае
В этом случае .Произвольную постоянную С определяем из начального условия
.Произвольную постоянную С определяем из начального условия  В результате находим
В результате находим  Тогда
Тогда  (2)
(2) это равенство упрощается.
это равенство упрощается. Вэтом случае
Вэтом случае  (3)Из начального условия
(3)Из начального условия  находим
находим  ~ Тогда
~ Тогда  (4)Равенство (4) называется законом изменения угловой скорости при равнопеременном вращательном движении тела. Далее
(4)Равенство (4) называется законом изменения угловой скорости при равнопеременном вращательном движении тела. Далее  • (5)
• (5) находим
находим  Тогда окончательно
Тогда окончательно  (6)
(6)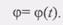 (1) Найдем распределение скоростей точек тела при его вращении. Воспользуемся при этом естественным способом задания движения точки. Рассмотрим движение какой-нибудь точки М тела. При вращении тела точка М будет описывать окружность, радиус которой обозначим R (рис. 2.21).
(1) Найдем распределение скоростей точек тела при его вращении. Воспользуемся при этом естественным способом задания движения точки. Рассмотрим движение какой-нибудь точки М тела. При вращении тела точка М будет описывать окружность, радиус которой обозначим R (рис. 2.21).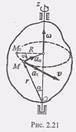 Составим уравнение движения точки М по ее траектории. За начало отсчета примем начальное положение Мо, а за положительное направление дуги s - направление отсчета угла поворота ф. Тогда уравнением движения точки М по ее траектории будет
Составим уравнение движения точки М по ее траектории. За начало отсчета примем начальное положение Мо, а за положительное направление дуги s - направление отсчета угла поворота ф. Тогда уравнением движения точки М по ее траектории будет 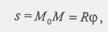 (2) а следовательно, проекция скорости точки М на направление касательной определится следующим образом:
(2) а следовательно, проекция скорости точки М на направление касательной определится следующим образом: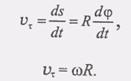 (4) Эту скорость точки М, в отличие от угловой скорости тела, часто называют линейной скоростью. Таким образом, линейная скорость какой-либо точки вращающегося твердого тела равна произведению угловой скорости тела на расстояние от этой точки до оси вращения. Вектор V скорости точки М направлен по касательной к окружности, которую описывает точка М, т.е. перпендикулярен к радиусу этой окружности. Модуль V вектора скорости V равен
(4) Эту скорость точки М, в отличие от угловой скорости тела, часто называют линейной скоростью. Таким образом, линейная скорость какой-либо точки вращающегося твердого тела равна произведению угловой скорости тела на расстояние от этой точки до оси вращения. Вектор V скорости точки М направлен по касательной к окружности, которую описывает точка М, т.е. перпендикулярен к радиусу этой окружности. Модуль V вектора скорости V равен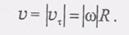 (5)
(5) и нормальное ускорения:
и нормальное ускорения: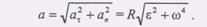 (7)
(7)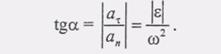 (8)
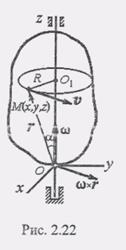
(8) Определим скорость произвольной точки М этого тела. Введем прямоугольную систему координат с началом на оси вращения и неизменно связанную с телом (рис. 2.22).В этом случае
Определим скорость произвольной точки М этого тела. Введем прямоугольную систему координат с началом на оси вращения и неизменно связанную с телом (рис. 2.22).В этом случае (1)
(1) Тогда для скорости точки М имеем(2)
Тогда для скорости точки М имеем(2) 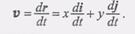
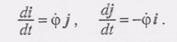
 (3)
(3)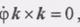 , найдем
, найдем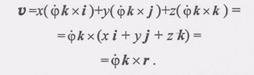
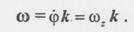 (5)
(5) (6)
(6)


