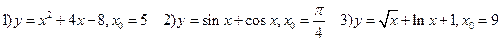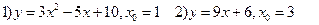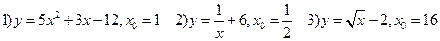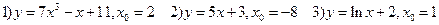Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: «Производная сложной функции»Содержание книги
Поиск на нашем сайте
Цель: сформировать умение находить производные сложных функций Теоретические сведения к практическому занятию: Производной функции
Производная сложной функции Производной n -го порядка называется производная от производной (n –1)-го порядка. Производные высших порядков вычисляются последовательным дифференцированием данной функции. Производная второго порядка Производная третьего порядка Пример. Найти производную функции Решение: Сложная степенная функция, независимая переменная есть v,
Самостоятельная работа: 1) Найти производные функций:
Содержание практического занятия: А. Ответить на вопросы: 1) Дайте определение производной функции. 2) Укажите формулу для нахождения производной сложной функции. 3) Дайте определение производной n-го и высшего порядка. Укажите формулы для нахождения. 4) Приведите примеры нахождения производных сложных функций. Б. Выполнить задания: 1) Найти производные функций:
2) Найти производные второго порядка:
3) Найти производные третьего порядка:
Тема: «Геометрический смысл производной» Цель: сформировать умение составлять уравнение касательной, знать геометрический смысл производной Теоретические сведения к практическому занятию: 23
Если кривая задана уравнением Уравнение касательной к кривой а уравнение нормали (М0N): Пример. Составить уравнение касательной и нормали к кривой Используем уравнения касательной (2) и нормали (3): 1) 2)
Подставим или
Самостоятельная работа: 1.Найти угловой коэффициент касательной к графику функции в точке с абсциссой х0
2.Составить уравнение касательной к графику функции в точке с абсциссой х0
Содержание практического занятия: А. Ответить на вопросы: 1) В чем заключается геометрический смысл производной функции. Укажите уравнения касательной и нормали к данной функции. 2) Приведите примеры нахождения уравнений касательной и нормали к данной функции. Б. Выполнить задания: 1.Составить уравнение касательной к графику функции в точке с абсциссой х0
2.Составить уравнение нормали к графику функции в точке с абсциссой х0
|
||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 180; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.73.149 (0.005 с.) |

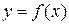 называется конечный предел отношения приращения функции
называется конечный предел отношения приращения функции 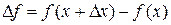 к приращению независимой переменной
к приращению независимой переменной 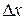 при стремлении последнего к нулю:
при стремлении последнего к нулю: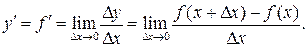
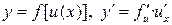 .
.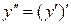 или
или 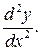
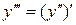 или
или 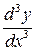 и т. д.
и т. д.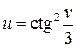
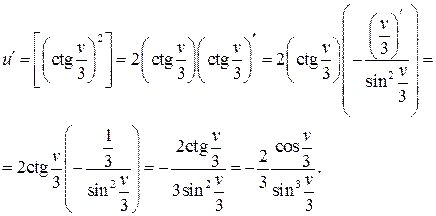
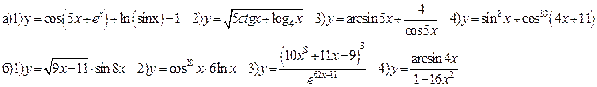
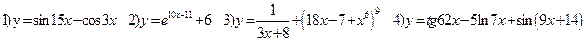
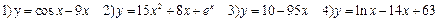
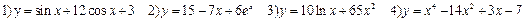
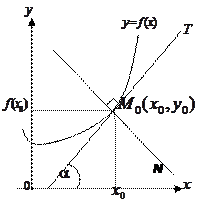 Геометрический смысл производной.
Геометрический смысл производной.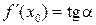 — угловой коэффициент касательной к графику функции в этой точке (
— угловой коэффициент касательной к графику функции в этой точке (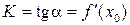 ).
).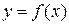
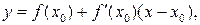
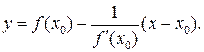
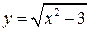 в точке с абсциссой х 0=-2.
в точке с абсциссой х 0=-2.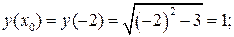
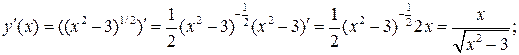
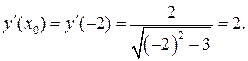
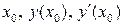 в уравнения и получим:
в уравнения и получим: 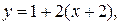
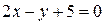 — уравнение касательной.
— уравнение касательной.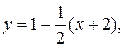 или
или 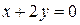 — уравнение нормали.
— уравнение нормали.