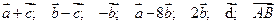Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: «операции над векторами. Разложение вектора»Содержание книги
Поиск на нашем сайте
Цель: сформировать определение понятия вектора в пространстве, равных векторов Теоретические сведения к практическому занятию: Пусть даны два произвольных вектора
Для любых векторов
Два ненулевых вектора называются противоположными, если их длины равны и они противоположно направлены. Вектором, противоположным нулевому вектору, считается нулевой вектор. Вектор Сумма нескольких векторов не зависит от того, в каком порядке они складываются. Правило построения суммы нескольких векторов называется правилом многоугольника.
Разностью векторов Произведением ненулевого вектора Для любых векторов
Вектор Если векторы Пример 1: Упростить выражения:
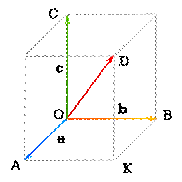
Векторы называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Если вектор Для сложения трех некомпланарных векторов используют правило параллелепипеда:
Если вектор Пример 2: Дан параллелепипед АВСМА1В1С1М1. Разложите вектор ВМ1 по векторам ВА, ВС и ВВ1. 38
Содержание практического занятия: А. Ответить на вопросы: 1) Сформулируйте правило сложения векторов. Изобразите графически правило сложения векторов. 2) Дайте определение противоположных векторов. Приведите примеры. 3) В чем заключается правило многоугольника при построении суммы векторов. 4) Дайте определение разности векторов. 5) Дайте определение произведения вектора на число. Чему равно произведение нулевого вектора на число? 6) Сформулируйте свойства сложения и произведения вектора на число. 7) Дайте определение компланарных векторов. Назовите признак компланарных векторов. 8) В чем заключается правило параллелепипеда сложения векторов? 9) Какой вектор можно разложить по трем данным некомпланарным векорам? Приведите примеры. Б. Выполнить задания: 1) Упростить выражения:
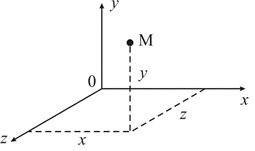
2) Дан тетраэдр АВСК. 1. Найти сумму векторов 2. Доказать 3) Дан параллелепипед АВСSА1В1С1S1. Назовите вектор, равный сумме векторов Тема: «Координаты вектора» Цель: сформировать определение понятия координат вектора, научиться находить координаты суммы, разности и произведения вектора на число, знать связь между координатами векторов и координатами точек Теоретические сведения к практическому занятию: Если через точку пространства проведены три попарно перпендикулярные прямые, на каждой из них выбрано направление, которое обозначается стрелкой и выбрана единица измерения отрезков, то задана прямоугольная система координат в пространстве. Прямые с выбранными на них направлениями называются осями координат, а их общая точка – началом координат. Обычно она обозначается буквой О. Оси координат обозначаются Ох, Оу, Оz и называются ось абсцисс, ось ординат и ось аппликат. Вся система координат обозначается Охуz. В прямоугольной системе координат каждой точке М пространства ставится в соответствие тройка чисел, которые называются ее координатами.
Пусть в пространстве задана прямоугольная система координат Охуz. На каждой из положительных полуосей от начала координат отложим единичный вектор – вектор, длина которого равна единице. Обозначим Коэффициенты Координаты равных векторов соответственно равны, т.е. если векторы Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов. Если Каждая координата разности двух векторов равна разности соответствующих координат этих векторов. Если Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число. Если Если точка А имеет координаты Пример. Даны векторы
40 Содержание практического занятия: А. Ответить на вопросы: 1) Каким образом можно задать прямоугольную систему координат в пространстве? Как обозначается данная система координат? Дайте определение координат точки. 2) Какие векторы называются координатными векторами? Какой вектор можно разложить по координатным векторам? 3) Дайте определение координат вектора. Каким образом обозначаются координаты вектора? 4) Чему равны координаты суммы, разности и произведения вектора на число? Запишите соответствующие формулы. 5) Какие координаты будет иметь вектор, если даны координаты двух точек? Б. Выполнить задания: 1) Даны векторы
2) Даны векторы
|
||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 184; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.86.38 (0.009 с.) |

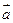 и
и 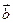 . Отложим от какой-нибудь точки А вектор
. Отложим от какой-нибудь точки А вектор 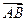 , равный
, равный 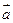 . Затем, от точки В отложим вектор
. Затем, от точки В отложим вектор  , равный
, равный 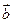 . Вектор
. Вектор 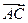 называется суммой векторов
называется суммой векторов 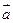 и
и 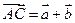 . Это правило сложения векторов называется правилом треугольника. Оно может быть также сформулировано и в другой форме: для любых трех точек А, В и С имеет место равенство
. Это правило сложения векторов называется правилом треугольника. Оно может быть также сформулировано и в другой форме: для любых трех точек А, В и С имеет место равенство 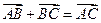 .
.
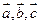 справедливы равенства:
справедливы равенства: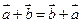 (переместительный закон)
(переместительный закон)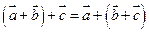 (сочетательный закон)
(сочетательный закон)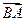 является противоположным вектору
является противоположным вектору 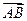 .
.
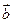 равна вектору
равна вектору 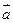 .
. 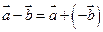
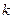 называется такой вектор
называется такой вектор 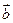 , длина которого равна
, длина которого равна 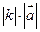 , причем векторы
, причем векторы 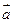 и
и 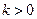 и противоположно направлены при
и противоположно направлены при 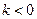 . Произведением нулевого вектора на любое число считается нулевой вектор. Произведение вектора
. Произведением нулевого вектора на любое число считается нулевой вектор. Произведение вектора 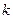 обозначается
обозначается 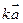 . Для любого числа
. Для любого числа 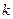 и любого вектора
и любого вектора 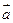 и
и 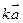 коллинеарны. Произведение любого вектора на число нуль есть нулевой вектор.
коллинеарны. Произведение любого вектора на число нуль есть нулевой вектор.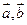 и любых чисел
и любых чисел 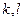 справедливы равенства:
справедливы равенства: (сочетательный закон)
(сочетательный закон)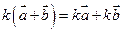 (первый распределительный закон)
(первый распределительный закон)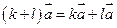 (второй распределительный закон)
(второй распределительный закон)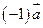 является вектором, противоположным вектору
является вектором, противоположным вектору 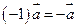 .
.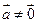 , то существует число
, то существует число 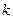 такое, что
такое, что  .
.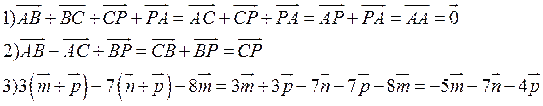
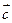 можно разложить по векторам
можно разложить по векторам 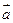 и
и 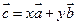 , где х и у – некоторые числа, то векторы
, где х и у – некоторые числа, то векторы  компланарны.
компланарны.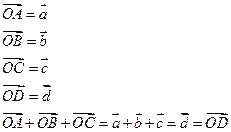
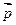 представим в виде
представим в виде 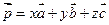 , где
, где 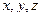 - некоторые числа, то вектор
- некоторые числа, то вектор 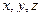 называются коэффициентами разложения. Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом.
называются коэффициентами разложения. Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом.
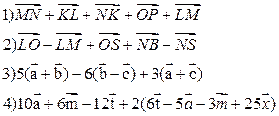
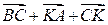
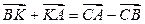

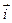 - единичный вектор оси абсцисс,
- единичный вектор оси абсцисс, 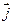 - единичный вектор оси ординат и
- единичный вектор оси ординат и 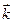 - единичный вектор оси аппликат. Векторы
- единичный вектор оси аппликат. Векторы 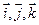 называются координатными векторами. Любой вектор
называются координатными векторами. Любой вектор 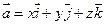 , причем коэффициенты разложения
, причем коэффициенты разложения 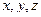 определяются единственным образом.
определяются единственным образом.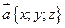 .
.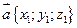 и
и 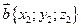 равны, то
равны, то 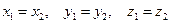 .
.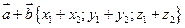
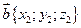 , то
, то 
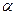 - данное число, то
- данное число, то 
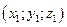 , а точка В имеет координаты
, а точка В имеет координаты 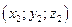 , то вектор АВ будет иметь координаты
, то вектор АВ будет иметь координаты 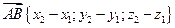 . Т.е. каждая координата вектора равна разности соответствующих координат его конца и начала.
. Т.е. каждая координата вектора равна разности соответствующих координат его конца и начала.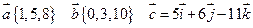 и точки
и точки  . Найти координаты векторов
. Найти координаты векторов 
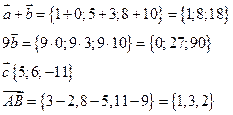
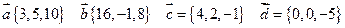 . Найти координаты векторов
. Найти координаты векторов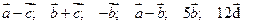
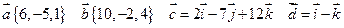 и точки
и точки 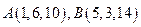 . Найти координаты векторов
. Найти координаты векторов