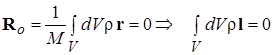Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вращение твердого тела вокруг закрепленной осиСодержание книги
Поиск на нашем сайте
В случае твердого тела, жестко скрепленного с закрепленных в подшипниках осью, устойчивое вращение возможно при любой ориентации этой оси и любом ее расположении относительно центра масс тела (рис. 10.6). Возможность. ускоренного движения центра масс и изменения момента импульса тела осью закрепленной оси обеспечивается силами реакции опоры, возникающими в подшипниках. В результате все точки твердого тела вращаются по окружностям, центры которых лежат на закрепленной оси.
Рис.4.6. Вращение твердого тела вокруг закрепленной оси
Каждый вращающийся элементарный объем тела дает в направленный по оси вращения момент импульса вклад, равный где l j – расстояние от рассматриваемого точечного объема до оси вращения. Суммирование вкладов (4.11) по всему объему тела приводит к сходному с (4.3) соотношению, связывающему момент инерции вращательного движения тела с его угловой скоростью, в котором коэффициент пропорциональности (момент инерции тела относительно закрепленной оси вращения является не тензорной, а скалярной величиной:
Дифференцирование по времени равенства (4.12) с учетом (3.5) позволяет связать угловое ускорение вращающегося на закрепленной оси твердого тела с суммарным моментом внешних сил, вычисляемом относительно неподвижной оси:
Наконец, кинетическая энергия тела, вращающегося вокруг закрепленной и неподвижной оси, вычисляется в соответствии с (4.7) вычисляется весьма просто:
Как правило, тела крепятся на осях вращения таким образом, чтобы центры их масс попадали на эти оси. Такое крепление существенным образом способствует уменьшению нагрузки на подшипники и облегчает расчеты моментов инерции (особенно в случаях симметричных тел).
Пример. Моменты инерции тел с цилиндрической симметрией. Рассчитать моменты инерции относительно оси симметрии следующих однородных тел с заданной массой: кольца радиусом R, полого цилиндра радиусом R и длиной h, сплошного цилиндра радиусом R и высотой h (рис. 4.7).
Рис.4.7. К расчету моментов инерции тел с цилиндрической симметрией Решение. Вклад в момент инерции кольца массой m его небольшого участка с массой Δ mj равен:
Все остальные участки дают аналогичные вклады, пропорциональных их массам. В результате полный момент инерции кольца равен:
Однородный полый цилиндр («труба») может рассматриваться как совокупность узких колец высотой Δ h j с массами Δ mj. Соответствии с (4.14) момент инерции каждого такого кольца равен: Суммирование вкладов в полный момент инерции всех элементарных колец позволяет найти момент инерции полого цилиндра:
Сплошной цилиндр может рассматриваться как совокупность вложенных друг в друга полых цилиндров со стенками малой толщины Δ r j. Вклад каждого такого элементарного полого цилиндра в общий момент согласно (10.15) равен:
Полный момент инерции вычисляется суммированием элементарных вкладов, для выполнения которого из-за нелинейности слагаемых по r j необходим переход к вычислению определенного интеграла:
В случае вычисления моментов инерции относительно осей, не проходящих через центр симметрии, весьма полезна теорема Штайнера.
Доказательство. Из рис.10.8 видно, что необходимые для вычисления моментов инерции расстояния (l j и l j’) от двух осей до текущего элементарного объема тела Δ m j связаны c расстоянием между осями вращения d очевидным соотношением: l j’ = l j + d. Его подстановка в (4.11) и (4.12) дает связь между моментами инерции тела относительно двух рассматриваемых осей:
Полученное выражение отличается от приведенного формулировке теоремы соотношения (4.16) одним слагаемым, представляющим собой скалярное произведение вектора d на интеграл по объему. Последний оказывается равным нулю, поскольку представляет собой результат проектирования на перпендикулярную осям вращения плоскость известного соотношения для радиус-вектора центра масс, который, очевидно, равен нулю системе отсчета, начало координат которой помещено в центр масс:
Рис.4.8. К доказательству теоремы Штейнера Вопросы и задачи для самостоятельной работы 1. Вычислить моменты инерции следующих геометрических примитивов (геометрические размеры заданы, полюс помещен в центр масс), считая, что масса равномерно распределена по объему: а) тонкий сферический слой, б) шар, в) круговой конус. 2. По наклонной плоскости, составляющей угол a с горизонтом, с высоты H без начальной скорости начинает скатываться а) шар, б) цилиндр радиуса R, массой M. Определить скорости каждого из тел в конце наклонного участки, если известно, что они катятся без проскальзывания. 3. Показать, что незакрепленный куб может совершать свободное устойчивое вращение вокруг любой оси, проходящей через его центр. Найти энергия вращения, если заданы масса куба, длина его ребра и угловая скорость. 5. Колебательные системы с одной Вблизи точек устойчивого равновесия линейные механические системы ведут себя аналогично пружинному маятнику и допускают общее стандартное описание вне зависимости от природы таких систем.
|
||||||
|
Последнее изменение этой страницы: 2020-12-19; просмотров: 192; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.007 с.) |

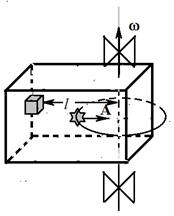
 , (4.11)
, (4.11) . (4.12)
. (4.12) . (4.13)
. (4.13) .
.
 .
. . (4.14)
. (4.14) .
.  . (4.15)
. (4.15) .
. .
. 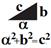
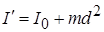 . (4.16)
. (4.16)
 .
.