Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение вынужденных колебанийСодержание книги
Поиск на нашем сайте
Анализ вынужденных колебаний под действием внешних сил традиционно ограничивается рассмотрением частного случая воздействия, изменяющегося во времени по гармоническому закону. Такой подход вполне оправдан, поскольку по теореме Фурье негармонические функции достаточно общего вида могут быть представлены как суперпозиции (суммой или интегралом) в гармонических. В случае линейных систем их отклик на суммарное внешнее воздействие может быть вычислен как сумма откликов на каждое из воздействий в отдельности. Т.о. оказывается достаточным проанализировать решение неоднородного уравнения вида:
Решение неоднородного линейного дифференциального уравнения (5.12), описывающего вынужденные колебания, может быть построено как сумма экспоненциально затухающего во времени решения однородного уравнения и частного решения неоднородного. Общее решение однородного уравнения было построено (5.8) и представляет собой затухающие во времени колебания на частоте, лишь немного отличающейся от частоты собственных свободных колебаний. Для нахождения частного решения неоднородного уравнения (5.12) целесообразно переписать правую часть в экспоненциальном виде:
и перейти для решения нового уравнения в комплексную плоскость, где частное решение уравнения
целесообразно искать в экспоненциальном виде на частоте вынуждающей силы:
и построить комплексное решение неоднородного уравнения:
Т.о. общее решение неоднородного уравнения построено как сумма общего решения однородного уравнения, представляющего собой затухающие во времени колебания на собственной частоте системы и частного решения неоднородного уравнения, представляющего собой вынужденные гармонические колебания на частоте вынуждающего воздействия на систему:
При возбуждении колебаний системы в первые моменты времени сосуществуют оба решения и реализуется переходный процесс. Из-за различия частот эти колебания то усиливают, то гасят друг друга. В системе возникают биения. По мере затухания во времени решения однородного уравнения колебательная система постепенно выходить на стационарный режим гармонических колебаний, происходящих только на частоты вынуждающей силы. Установившиеся колебания происходят на частоте вынуждающей силы и реализуются в линейных системах на больших временах после начала действия внешних сил, когда решение однородного уравнения, представляющего собой затухающие колебания на собственной частоте системы, оказывается пренебрежимо малым. Зависимость амплитуды вынужденных колебаний от частоты внешнего воздействия носит ярко выраженный резонансный характер (рис.5.5).
При резонансе система совершает вынужденные колебания на частоте вынуждающей силы, фаза колебаний которой оказывается такой, что ее мощность все время остается положительной, что обеспечивает эффективную передачу энергии в колеблющуюся систему.
Вопросы и задачи для самостоятельной работы. 1. Шарик падает без начальной скорости с высоты H на горизонтальную плоскость и начинает скакать, теряя при каждом ударе k < 1 часть своей кинетической энергии. Построить фазовый портрет движения описанной системы. 2. Показать, что при совпадении корней характеристического уравнения присоединенное решение (11.11) обращает дифференциальное уравнение в верное тождество. 3. Через сплошной однородный шар массой M продета горизонтальная ось, пронизывающая его на расстоянии R/2 от центра. Найти период малых колебаний шара вокруг горизонтальной оси. 4. Небольшой груз массой m, несущий электрический заряд q, висит неподвижно на вертикальной нити длиной l. Мгновенно включается горизонтальное электрическое поле E. Записать уравнение возникших незатухающих колебаний и его решение. 5. Однородная доска длиной L лежит на двух вращающихся навстречу друг другу роликах, расстояние между осями которых равен l. Коэффициент трения доски о поверхность каждого из роликов равен μ. Найти период горизонтальных колебаний доски. 6. Электрически заряженная частица с зарядом q и массой m нанизана на тонкий обруч и может скользить вдоль нее без трения.Частица совершает малые колебания в нижней части кольца с частотой ω. Какое вертикальное электрическое поле необходимо создать для того, чтобы частица могла совершать малые колебания с вдвое меньшей частотой? 7. После того, как частота ω действия на линейную колебательную систему гармонической вынуждающей силы увеличилась в 2 раза амплитуда вынужденных колебаний возросла в 2 раза. Чему равна резонансная частота линейной колебательной системы?
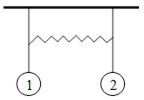
Механические волны Связанные маятники Обладающая двумя степенями свободы система из двух связанных одномерных маятников (рис. 6.1) описывается системой двух линейных дифференциальных уравнений.
Рис.6.1. Связанные маятники Система дифференциальных уравнений, описывающих свободные и вынужденные колебания связанных маятников, имеет вид: Для решения системы описывающих связанные маятники уравнений удобно перейти к новым переменным, представляющим собой сумму и разность решений исходных уравнений. Переход к новым неизвестным
превращает (6.1) в систему «расцепленных» друг от друга однородных уравнений: Решение задачи (6.3) о связанных маятниках в случае свободных колебаний для переменных (6.2) имеет вид: Полученный результат (6.4) показывает, что в рассматриваемой системе возможны две собственные моды гармонических колебаний. Первая собственная мода реализуется, когда маятники колеблются в фазе: Вторая собственная мода соответствует встречным колебаниям маятников, происходящих с одинаковыми амплитудами: При первоначальном смещении одного из маятников вместо решений (6.5) и (6.6) в виде гармонических колебаний возникают биения, при которых маятники поочередно раскачиваются и переходят в состояние покоя:
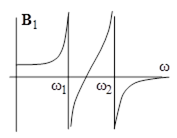
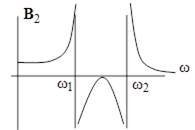
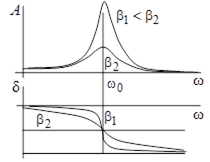
Вынужденные колебания системы связанных маятников происходят на частоте вынуждающей силы с амплитудами, имеющими явно резонансный вид и достигающими максимумов на частотах вынуждающей силы, совпадающих с частотами мод гармонических колебаний системы. В координатах (12.2) установившиеся вынужденные колебания в системе связанных маятников происходят по гармоническому закону: Решение (12.8)задачи об установившихся колебаниях в исходных «естественных» координатах имеет вид зависимостей, имеющих две резонансные частоты (рис. 12.2):
Рис. 6.2. Резонансы при вынужденных
|
||||||
|
Последнее изменение этой страницы: 2020-12-19; просмотров: 125; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.178.81 (0.01 с.) |

 . (5.11)
. (5.11)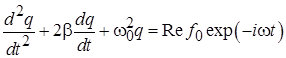
 (5.13)
(5.13)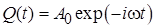 . (5.14)
. (5.14)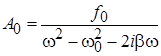 ,
,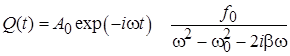 .
. 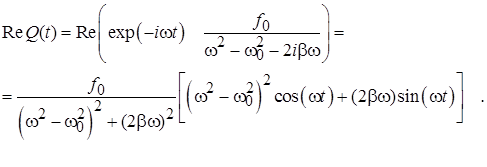
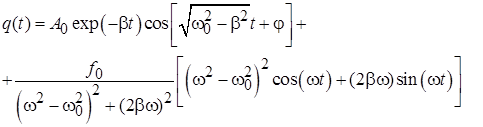

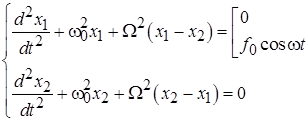 ,
, 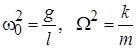 (6.1)
(6.1)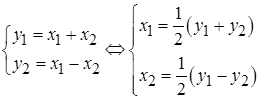
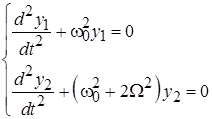 . (6.3)
. (6.3) (6.4)
(6.4)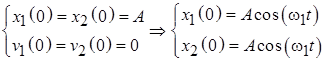 (6.5)
(6.5)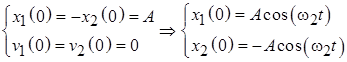 (6.6)
(6.6)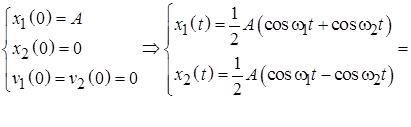
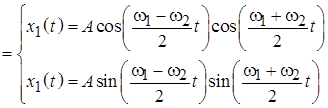 . (6.7)
. (6.7)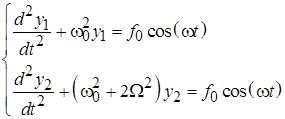
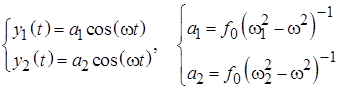 . (6.8)
. (6.8)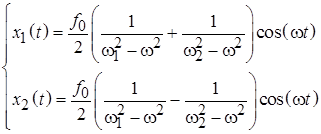 (6.9)
(6.9)