Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамика систем материальных точекСодержание книги
Поиск на нашем сайте
Чирцов А. С. Ч65 Классическая механика систем материальных точек: учеб. пособие. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2020. 65 с.
ISBN 978-5-7629-????-?
Являясь отдельным и самостоятельным изданием для студентов технических специальностей, в то же время это составная часть четырехуровневого учебника по физике, ориентированного на максимально широкий круг читателей. Ориентировано на студентов технических университетов, изучающих курс общей физики, и содержит материал, развивающий и углубляющий базовые знания по классической механике материальной точки, изложенные в первой части курса классической механики для студентов технических университетов, обобщая ранее сформулированные для описания движения точечных тел идеи на случай описания механики классических систем материальных точек. Также может быть рекомендовано наиболее мотивированным и подготовленным учащимся старших классов школ и гимназий, желающим расширить и углубить знания школьного курса и получить дополнительную подготовку к участию в олимпиадах и решению усложненных задач на ЕГЭ по физике. УДК 531(07 ББК В 21 я7
Рецензенты: зав. кафедрой Общей физики 1 СПбГУ, д-р физ.-мат. наук И.Ч.Машек; проф. ФТФ ИТМО, д-р физ.-мат. наук С.К.Стафеев
Утверждено
Уважаемый читатель! Если Вы держите в руках это пособие, то это скорее всего значит, что Вы прошли стартовую часть не легкого и достойного пути в мир физики и успешно освоили первую часть пособия, посвященную классической механике материальной точки. Настоящее пособие нацелено на то, чтобы помочь Вам продолжить успешно начатый процесс и познакомиться с целым рядом весьма содержательных идей классического описания систем материальных точек, которые основываются на уже изученных принципах механики точечных тел. Форма пособия несколько необычна. Это не учебник по физике и не задачник. Представленный в пособии материал максимально приближен к конспекту лекций хорошего студента: в нем содержатся основные идеи курса, записанные на максимально приспособленном для изложения физики весьма информационно емком, точном и кратком языке – языке математики. В качестве пояснений приведены схематичные рисунки и очень краткие тексты в почти «лозунговой» форме, ставшей се рисунки в количестве, не меньшем, чем приведенные в данном пособии. Пособие содержит материалы, соответствующие второй трети лекционного курса по физике на 1 семестре. Мне хочется пожелать читателю не только успехов в предстоящем изучении курса физики, но и получения истинного удовольствия в освоении того понимания, которое было достигнуто человечеством в ходе решения одной из самых амбициозных задач – понимания того, как устроен окружающий нас мир. На этом нелегком, но достойном пути Вам может понадобиться реальная помощь. Не исключено, что материалов этого пособия Вам будет недостаточно. В настоящее время легкодоступен весьма широкий набор печатных и электронных изданий по классической механике. В подготовленном для Вас списке перечислены те, которые могут оказаться и окажутся наиболее полезными для Вас. Автор
Рекомендуемая литература 1. Е.И. Бутиков, А.С. Кондратьев. Физика. В 3-х томах. Том 1. Механика. -- Фиматлит. 2018., 352 с. 2. Ч. Киттел, В. Найт, М. Рудерман. Берклеевский курс физики. Том 1. М. Механика. ----- Москва. Издательство «Наука», 1983, 210 с. 3. Д.В. Сивухин. Общий курс физики. А 5 т. Том 1. Механика. --- М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. - 560 с. 4. Р. Фейнман ., Р. Лейтон, М. Сэндс. Фейнмановские лекции по физике. Выпуск 1. Современная наука о природе. Законы механики. Выпуск 2. Пространство. Время. Движение (издание 5). — Эдиториал УРСС. 5. А.С. Чирцов. Классическая механика материальной точки. --- СПбГЭТУ «ЛЭТИ» 2019, 87 с. 6. А.С. Чирцов. «Кинематика», «Динамика», «Космическая механика» --- on-line курсы в видеотеке Лекториум.
Центр масс Для системы материальных точек может быть введен центр масс – точка, классическое уравнение движения для которой совпадает со вторым законом Ньютона для точечного тела с массой, равной суммарной массе системы M, при условии действия на нее лишь внешних сил, приложенных к элементам системы.
Помимо центра масс для описания движения системы материальных точек как целого удобно ввести скорость V и ускорение A центра масс (первая и вторая производные по времени от радиус-вектора R) и полный импульс системы P.
Из определений (7.2) и (7.3) следует сходная с обсуждавшийся в механике материальной точки (см. (4.9) из [5]) связь между скоростью центра масс, суммарной массой и импульсом системы:
Дифференцирование по времени полученной связи (1.4) импульса системы со скоростью ее центра масс позволяет получить аналог хорошо известной для материальной точки связи (см. (4.7) - (4.9) из [5]) между ускорением центра масс системы и скоростью изменения ее полного импульса:
Задача двух тел Переход в систему центра масс при анализе движения системы из двух взаимодействующих тел позволяет свести задачу к описанию движения одной частицы с приведенной массой. Система уравнений движения двух взаимодействующих между собой тел, не испытывающих воздействие внешних сил имеет вид: Переход от традиционной системы (2.1) к уравнениям в системе отсчета, связанной с центром масс, осуществляется с помощью следующих равенств: В введенной согласно (2.2) системе уравнение движения приобретает вид который путем введения приведенной массы μ приводится к форме, аналогичный уравнению движения одной частицы: Пример. Двойная звезда. Численное моделирование показывает, что компоненты двойной звезды, совершая периодическое движение вокруг общего центра масс, всегда удалены от него на расстояния, обратно пропорциональные их массам. В случае одинаковых масс (рис. 2.1) обе компоненты движутся по одинаковым пересекающимся траекториям. Если массы компонент дойной звезды различны, то более массивная движется по траектории с меньшими характерными размерами. В этом случае более компактная траектория может быть как вложена в большую (рис. 2.2), так и может с ней пересекаться. Во всех случаях компактные компоненты двойной звезды никогда не сталкиваются друг с другом из-за того, то всегда располагаются на различных концах отрезка переменной длины, походящего через их общий центр масс. Методы аналитического решения уравнения движения (2.3) в случае гравитационного взаимодействия тел (см. (4.21) из [5]) будут рассмотрены в разделе, посвященном закону всемирного тяготения.
Общие положения При переходе от механики систем материальных точек к писанию твердого тела дискретное распределение точечных масс заменяется на непрерывное распределение и, следовательно, суммирование по точечным телам переходит в интегрирование по объему тела. При этом сохраняются теоремы о скоростях изменения импульса и момента импульса систем, которые дают шесть скалярных уравнений движения, достаточных для описания движения твердого тела, обладающего шестью степенями свободы.
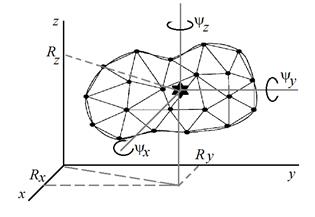
Так определяемое абсолютно твердое тело является моделью, а не реальным физическим объектом. Приписываемые Определением 3.1 свойства противоречат как фундаментальным требованиям теории относительности (в случае реального существования абсолютно твердое тело могло бы использоваться для мгновенной передачи сигнала от одной точки пространства к другой удаленной от исходной точке), так и основаниям квантовой механики (признающим вопреки 3.1) невозможность одновременного наличия у частицы точного значения координат и соответствующих проекций импульса). Несмотря на сказанное, рассматриваемая модель находит широчайшее применение для простого и удобного (но не абсолютно точного) описания движения макроскопических тел, форма которых слабо изменяется с течением времени. Абсолютно твердое тело имеет шесть степеней свободы. Его положение в пространстве можно полностью описать, задав, например, положение центра масс (три числа) и три угла поворота тела вокруг трех координатных осей, проведенных через центр масс (рис. 3.1). Для полного описания движения абсолютно твердого тела необходимо иметь шесть скалярных (или три векторные) уравнения движения.
Рис. 3.1. Задание положения твердого тела в пространстве
Как правило, составляющие реальные почти твердые тела частицы (атомы, молекулы, ионы) расположены достаточно плотно. Это позволяет в рамках модели абсолютно твердого тела приближенно перейти от ранее рассматривавшихся дискретных распределений точечных тел в системе к их непрерывному распределению и ввести понятие плотности вещества твердого тела:
В соотношениях (3.2) при переходе к записи результатов в виде производной и/или интеграла использовано приближенное равенство из-за того, что в рассматриваемой ситуации объем ячейки пространства не может быть устремлен к нулю в математическом смысле из-за дискретности распределения вещества в объеме тела. В результате в механике твердого тела операции дифференцирования и интегрирования по объемам носят приближенный характер и на самом деле сводятся к делению на физически бесконечно малый объем или суммированию по малым (в физическом смысле) объемам. Определения полных импульса (1.6) и момента импульса (1.12) абсолютно твердого тела, даются в соответствии с идеологией, рассмотренной при обсуждении смысла соотношения (3.3): Для получения полной информации о движении абсолютно твердого тела могут быть использованы две теоремы о скоростях изменения полного импульса системы (1.6) и момента этого импульса (1.12). Соответствующая пара векторных равенств дает шесть независимых уравнений движения, полностью определяющие поведение системы с шестью степенями свободы: Статика Твердое тело находится в равновесии, если обе суммы действующих на него сил и приложенных моментов сил равны нулю. Условие равновесия твердого тела имеет вид, непосредственно вытекающий из (3.5): В статике выбор полюса, относительно которого вычисляются моменты в (9.6), произволен. Возможность смещения полюса на произвольный вектор R следует из условия равенства нулю суммы приложенных к телу сил: Важным приложением задач статики является расчет условий равновесия абсолютно твердого тела заданной формы в поле сил тяжести. Некоторая сложность учета этой силы связана с тем, что она является распределенной, т.е. действующей на каждый их элементов тела, расположенных в точках r j. Эту распределенную силу удобно заменить равнодействующей
точка приложения которой определяется требованием равенства ее момента суммарному моменту распределенной силы:
Доказательство теоремы непосредственно вытекает из условия равенства моментов (3.7) и определения центра масс системы материальных точек (1.2). Разумеется, теорема справедлива лишь в одинаковости ускорения свободного падения во всех точках пространства, занимаемого рассматриваемым телом. Например, в случае тела, размеры которого сопоставимы с радиусом шарообразной планеты, результат (3.8) не является верным.
Пример. Устойчивость незакрепленной опоры. Однородная доска длиной L и массой M лежит на краю берега так, что над водой свешивается четверть ее длины (рис. 3.5). Тщательно не изучивший основы статики студент массой m задумчиво идет по доске в направлении к реке, стремясь подойти как можно ближе к краю доски. В какой точке своего пути студент поймет, что даже классическая физика в некоторых жизненных ситуациях оказывается весьма полезной?
Рис. 3.5. К расчету устойчивости незакрепленной опоры
Решение. Рассмотри описанную систему тел в критический момент начала переворота доски, когда ее лежащая на берегу часть начинает отрываться от поверхности земли. В этот момент силы реакции, возникавшие в результате взаимодействия доски с поверхностью берега обращаются в ноль во всех точках, кроме крайней точки «О», вокруг которой начинается опрокидывание доски. Действующая на доску сила тяжести приложена к ее центру тяжести, расположенному на расстоянии L/4 от оси вращения, студент давит на доску в точке его нахождения. Искомое критическое положение студента легко определяется из условия равенства моментов сил относительно точки «О» в последний момент перед переворотом доски:
Разумеется, полученный результат применим лишь в случае m > M /2. При невыполнении приведенного неравенства ситуация окажется еще более трагичной: задумчивый студент окажется в воде без спас средства в виде плавающей доски, которая останется на берегу. Ограничения применимости модели абсолютно твердого тела могут возникнуть уже на уровне решения задач статики. Например, в случае бруска с известной, покоящегося не на двух, а на трех точечных опорах (рис. 3.6) возникает статически неопределенная задача с тремя неизвестными силами реакции, для решения которой двух условий (3.6) оказывается недостаточно. Решение описанной задачи требует учета возникающих в бруске деформаций, методы расчета которых изучаются в специальных разделах физики и материаловедения.
Рис. 3.6. Пример системы, не допускающей корректного описания
Кинетическая энергия
Доказательство. В соответствии с общим выражение для кинетической энергии системы материальных точек (1.15) кинетическая энергия твердого тела может быть разделена на два слагаемых, соответствующих энергиям поступательного движения и вращения: В отличие от стандартной формы записи кинетической энергии твердого тела (4.6) результат вычислений (4.7) записан в виде, иллюстрирующем глубокую аналогию между уравнениями поступательного и вращательного движения. В случае явного задания компонент векторов и элементов матриц результат (10.7) может быть записан в виде:
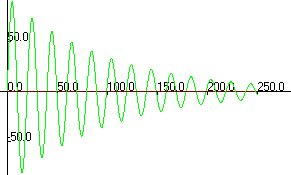
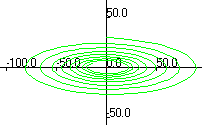
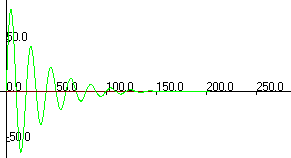
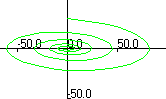
Затухающие колебания Учет действия диссипативных сил (например, линейной по скорости силы вязкого трения) делает колебания затухающими, фазовый портрет которых перестает быть замкнутой кривой, превращаясь в скручивающуюся спираль (рис. 5.3) Уравнение движения линейного осциллятора при наличии вязкого трения (5.3) проще решать в частном случае начальных условий, соответствующих случаю кратковременного толчка системы, первоначально покоившейся в положении равновесия: q (0) = 0, p (0) = p 0. В случае действия диссипативных сил характеристическое уравнение и его корни приобретают вид:
В результате общее решение однородного уравнения (11.3) усложняется по сравнению с (5.5): В случае малых величин диссипативных сил корни характеристического уравнения (5.7) оказываются комплексными, а решение (5.8) описывает затухающие колебания. Частота затухающих колебаний (5.9) оказывается меньше частоты колебаний в случае отсутствия энергетических потерь (5.6). Появление нового эффекта уменьшения амплитуды колебаний с течением времени предопределяет ведение новых дополнительных характеристик процесса. Временем жизни колебаний называется временной интервал на котором амплитуда колебаний уменьшается в e раз: Легко заметить, что время жизни процесса определяется отношением массы совершающего колебания тела к эффективному коэффициенту вязкого трения. Другой популярной характеристикой процесса затухания колебаний я является логарифмический декремент затухания:
Добротностью осциллятора называется отношение запасенной энергии к энергии, теряемой за период): Добротность просто выражается через с логарифмическим декрементом затухания (обязательно найдите эту связь!).
Рис. 5.3. Затухающие колебания и их фазовые портреты
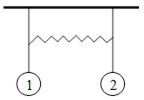
Механические волны Связанные маятники Обладающая двумя степенями свободы система из двух связанных одномерных маятников (рис. 6.1) описывается системой двух линейных дифференциальных уравнений.
Рис.6.1. Связанные маятники Система дифференциальных уравнений, описывающих свободные и вынужденные колебания связанных маятников, имеет вид: Для решения системы описывающих связанные маятники уравнений удобно перейти к новым переменным, представляющим собой сумму и разность решений исходных уравнений. Переход к новым неизвестным
превращает (6.1) в систему «расцепленных» друг от друга однородных уравнений: Решение задачи (6.3) о связанных маятниках в случае свободных колебаний для переменных (6.2) имеет вид: Полученный результат (6.4) показывает, что в рассматриваемой системе возможны две собственные моды гармонических колебаний. Первая собственная мода реализуется, когда маятники колеблются в фазе: Вторая собственная мода соответствует встречным колебаниям маятников, происходящих с одинаковыми амплитудами: При первоначальном смещении одного из маятников вместо решений (6.5) и (6.6) в виде гармонических колебаний возникают биения, при которых маятники поочередно раскачиваются и переходят в состояние покоя:
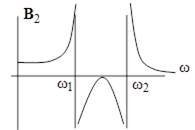
Вынужденные колебания системы связанных маятников происходят на частоте вынуждающей силы с амплитудами, имеющими явно резонансный вид и достигающими максимумов на частотах вынуждающей силы, совпадающих с частотами мод гармонических колебаний системы. В координатах (12.2) установившиеся вынужденные колебания в системе связанных маятников происходят по гармоническому закону: Решение (12.8)задачи об установившихся колебаниях в исходных «естественных» координатах имеет вид зависимостей, имеющих две резонансные частоты (рис. 12.2):
Рис. 6.2. Резонансы при вынужденных
Заключение Вот и подошла к концу вторая часть курса классической механики, посвященная методам описания и расчетов движения материальной точки. В рамках изложенного материала на базе первой части курса, посвященной классической механике материальной точки, были сформулированы новые идеи, посвященные методам классического описания движения тел конечных размеров. Все эти новые методы логично, с математической строгостью вытекали из ранее изложенного курса механики материальной точки. Однако, я вряд ли ошибусь с прогнозом того, что для значительной доли читателей изложенный здесь материал не показался слишком легким. Причина этого состояла в том, что изложение данного раздела физики было более математизировано, чем изложение первой части. Теперь можно открыть маленький секрет – в этом разделе Вы не столько изучали физику, сколько продолжали знакомиться со способами ее изложения на языке математики и учились не только понимать этот язык, но и активно им пользоваться. Возможно, это вызывало трудности. Но для того трудности и существуют, чтобы их успешно преодолевать. Если Вы добрались до этой заключительной страницы, хочется надеяться, что победителями оказались Вы, а не математические значки и формулы, которые, поверьте, уже довольно скоро начнут Вам казаться весьма привлекательными, понятными и безальтернативными в случае сколько-нибудь серьезного разговора о физике. Если эти слова Вас не слишком удивили и не вызвали у Вас страха или ужаса, значит все хорошо. Значит Вы на правильном пути. Значит наступит время, когда Вам захочется перейти на следующий (четвертый) уровень сложности нашего многоуровневого учебника по физике. Если же при изучении основ механики по этому пособию Вас постигла неудача и математический формализм и лаконичные замечания по физическому смыслу формул не были Вами осознана до конца, ну что же… Попробуйте заглянуть в материалы, представленные на втором или даже первом уровне сложности изложения. Возможно там Вы найдете то, что более соответствует Вашему уровню подготовки и менталитету. Удачи и успехов всем, кто причитал эту страницу! До новых встреч!
А.С.Чирцов
Содержание Уважаемый читатель! 3 7. Динамика систем материальных точек. 5 7.1. Рассмотрение движения системы взаимодействующих частиц на основе законов Ньютона 5 7.2. Центр масс. 7 9.3. Закон сохранения импульса системы частиц. 8 7.4. Закон сохранения момента импульса системы материальных точек. 11 7.5. Закон сохранения механической энергии в потенциальных системах. 13 Вопросы и задачи для самостоятельной работы.. 17 8. Примеры движения простых систем материальных точек. 19 8.1. Задача двух тел. 19 8.2. Упругое столкновение двух тел. Лобовой удар. 20 10.3. Произвольные упругие столкновения. 21 8.4. Неупругие и сверх упругие столкновения. 22 8.5. Движение тела с переменной массой. 23 Вопросы и задачи для самостоятельной работы.. 23 9. МОДЕЛЬ Абсолютно твердоГО телА. Статика. 25 9.1. Общие положения. 25 9.2. Равнодействующая сил, приложенных к твердому телу. 27 9.3. Статика. 29 9.4. Простейшие формы движения твердого тела. 32 9.5. Произвольное движение твердого тела. 33 Вопросы и задачи для самостоятельной работы.. 34 10. Абсолютно твердое тело. Динамика. 35 10.1. Момент импульса свободного твердого тела, тензор инерции. 35 10.2. Кинетическая энергия. 39 10.3. Свободное вращение твердого тела. 39 10.4. Простейшие движения твердого тела с неподвижной точкой опоры при наличии внешних сил. 42 11. Колебательные системы с одной степенью свободы.. 48 11.1. Вывод простейшего уравнения гармонических колебаний. 48 11.2. Решение простейшего уравнения незатухающих гармонических колебаний. 50 11.3. Затухающие колебания. 51 11.4. Апериодический режим при затухающих колебаниях. 53 11.5. Уравнение вынужденных колебаний. 54 Вопросы и задачи для самостоятельной работы. 57 12. Механические волны.. 58 12.1. Связанные маятники. 58 12.2 Бесконечная цепочка из связанных маятников. 60 12.4 Продольные волны в упругой среде. 63 12.5. Плоские монохроматические волны.. 64 Заключение. 66 Содержание. 67
Чирцов А С
Чирцов А. С. Ч65 Классическая механика систем материальных точек: учеб. пособие. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2020. 65 с.
ISBN 978-5-7629-????-?
Являясь отдельным и самостоятельным изданием для студентов технических специальностей, в то же время это составная часть четырехуровневого учебника по физике, ориентированного на максимально широкий круг читателей. Ориентировано на студентов технических университетов, изучающих курс общей физики, и содержит материал, развивающий и углубляющий базовые знания по классической механике материальной точки, изложенные в первой части курса классической механики для студентов технических университетов, обобщая ранее сформулированные для описания движения точечных тел идеи на случай описания механики классических систем материальных точек. Также может быть рекомендовано наиболее мотивированным и подготовленным учащимся старших классов школ и гимназий, желающим расширить и углубить знания школьного курса и получить дополнительную подготовку к участию в олимпиадах и решению усложненных задач на ЕГЭ по физике. УДК 531(07 ББК В 21 я7
Рецензенты: зав. кафедрой Общей физики 1 СПбГУ, д-р физ.-мат. наук И.Ч.Машек; проф. ФТФ ИТМО, д-р физ.-мат. наук С.К.Стафеев
Утверждено
Уважаемый читатель! Если Вы держите в руках это пособие, то это скорее всего значит, что Вы прошли стартовую часть не легкого и достойного пути в мир физики и успешно освоили первую часть пособия, посвященную классической механике материальной точки. Настоящее пособие нацелено на то, чтобы помочь Вам продолжить успешно начатый процесс и познакомиться с целым рядом весьма содержательных идей классического описания систем материальных точек, которые основываются на уже изученных принципах механики точечных тел. Форма пособия несколько необычна. Это не учебник по физике и не задачник. Представленный в пособии материал максимально приближен к конспекту лекций хорошего студента: в нем содержатся основные идеи курса, записанные на максимально приспособленном для изложения физики весьма информационно емком, точном и кратком языке – языке математики. В качестве пояснений приведены схематичные рисунки и очень краткие тексты в почти «лозунговой» форме, ставшей се рисунки в количестве, не меньшем, чем приведенные в данном пособии. Пособие содержит материалы, соответствующие второй трети лекционного курса по физике на 1 семестре. Мне хочется пожелать читателю не только успехов в предстоящем изучении курса физики, но и получения истинного удовольствия в освоении того понимания, которое было достигнуто человечеством в ходе решения одной из самых амбициозных задач – понимания того, как устроен окружающий нас мир. На этом нелегком, но достойном пути Вам может понадобиться реальная помощь. Не исключено, что материалов этого пособия Вам будет недостаточно. В настоящее время легкодоступен весьма широкий набор печатных и электронных изданий по классической механике. В подготовленном для Вас списке перечислены те, которые могут оказаться и окажутся наиболее полезными для Вас. Автор
Рекомендуемая литература 1. Е.И. Бутиков, А.С. Кондратьев. Физика. В 3-х томах. Том 1. Механика. -- Фиматлит. 2018., 352 с. 2. Ч. Киттел, В. Найт, М. Рудерман. Берклеевский курс физики. Том 1. М. Механика. ----- Москва. Издательство «Наука», 1983, 210 с. 3. Д.В. Сивухин. Общий курс физики. А 5 т. Том 1. Механика. --- М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. - 560 с. 4. Р. Фейнман ., Р. Лейтон, М. Сэндс. Фейнмановские лекции по физике. Выпуск 1. Современная наука о природе. Законы механики. Выпуск 2. Пространство. Время. Движение (издание 5). — Эдиториал УРСС. 5. А.С. Чирцов. Классическая механика материальной точки. --- СПбГЭТУ «ЛЭТИ» 2019, 87 с. 6. А.С. Чирцов. «Кинематика», «Динамика», «Космическая механика» --- on-line курсы в видеотеке Лекториум.
Динамика систем материальных точек Классическая механика материальной точки легко обобщается на конечные системы точечных тел. В таких системах может быть введена особая точка центр масс –, движение которой оказывается весьма сходным с движением материальной точки с массой, равной суммарной массе системы.
1.1. Рассмотрение движения системы взаимодействующих частиц В случае взаимодействующих друг с другом и с внешним миром систем материальных точек классическое уравнение движения (4.10 в [5]) принимает вид системы сцепленных друг с другом обыкновенных дифференциальных уравнений второго порядка: Рассмотрение задачи описания поведения системы материальных точек на основе решения системы дифференциальных уравнений движения для каждой из частиц в рамках классической механики привело к детерминизму Лапласа. На основании теоремы единственности решения системы из N сцепленных дифференциальных уравнений второго порядка с 2 N начальными условиями был сделан вывод о принципиальной возможности однозначного предсказания (расчета) положений и скоростей составляющих весь наблюдаемый мир материальных точек по и начальным механическим состояниям. Ошибочность попыток описанного обоснования детерминистического учения состояла в абсолютизации законов классической механики.
Пример 1.1. Система грузов на идеальных блоках. Через невесомый блок без трения в оси перекинута невесомая нерастяжимая веревка, к концам которой привязаны грузы с одинаковыми массами m, расположенные на отсчитываемом вдоль вертикали расстоянии h друг от друга (рис. 1.1). Система покоилась до тех пор, пока на веревку не посадили дрессированную обезьяну, которая сразу схватила веревку и начала перебирать лапами так, чтобы всегда оставаться на месте. Через какое время грузы после начала движения грузы окажутся на одной высоте? Решение. Для каждого из трех движущихся тел (грузы и обезьяна) следует изобразить все действующие силы (рис. 1.1) и записать свое классическое уравнение движения (второй закон Ньютона в векторной форме):
Рис. 1.1. Иллюстрации к постановке задачи в Примере 1.1 и центральному этапу ее решения
Предположив, то грузы движутся навстречу друг другу, зададим направления их ускорений так, как показано на рисунке. Записанные векторные равенства удобно спроектировать на направления движения каждого их тел (координатные оси для правого и левого грузов направлены противоположно). Проекции записанных выше векторных равенств на направления движения грузов имеют вид системы, число неизвестных в которой превосходит количество уравнений:
Из условия не растяжимости нити
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-19; просмотров: 124; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.62.5 (0.017 с.) |

 ISBN 978-5-7629-????-? © СПбГЭТУ «ЛЭТИ», 2020
ISBN 978-5-7629-????-? © СПбГЭТУ «ЛЭТИ», 2020
 (1.2)
(1.2)
 (1.3)
(1.3) . (1.4)
. (1.4)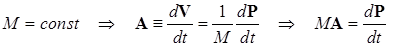 (1.5)
(1.5)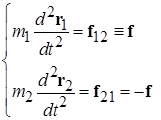 . (2.1)
. (2.1) (2.2)
(2.2)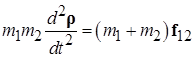 ,
, 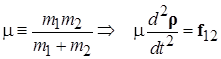 . (2.3)
. (2.3)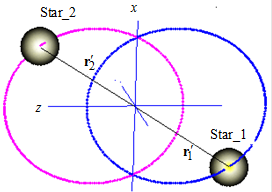


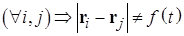 (3.1)
(3.1)
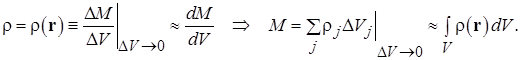 (3.2)
(3.2) 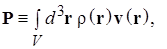 (3.3)
(3.3)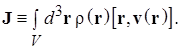 (3.4)
(3.4) 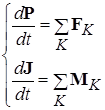 (3.5)
(3.5)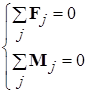 (3.6)
(3.6)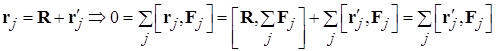 .
. 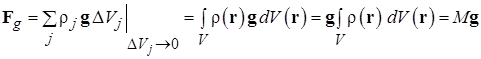 ,
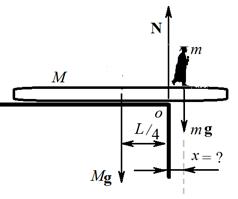
,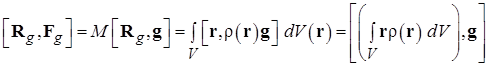 . (3.7)
. (3.7)
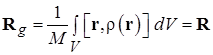 . (3.8)
. (3.8)
 .
.
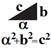
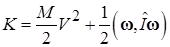 . (4.6)
. (4.6)
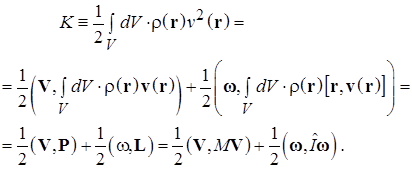 (4.7)
(4.7)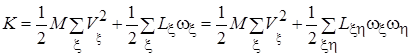 . (4. 8)
. (4. 8)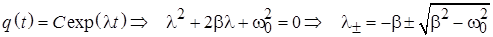 . (5.7)
. (5.7)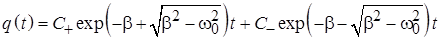 (5.8)
(5.8)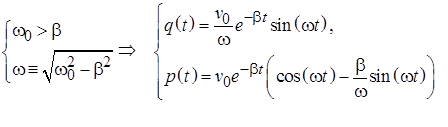 . (5.9)
. (5.9)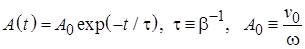 .
.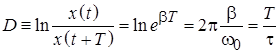 .
.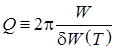
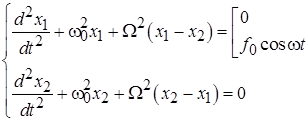 ,
,  (6.1)
(6.1)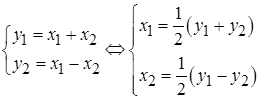
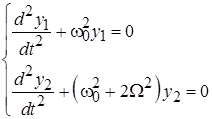 . (6.3)
. (6.3) (6.4)
(6.4)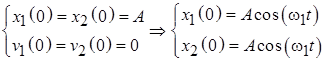 (6.5)
(6.5)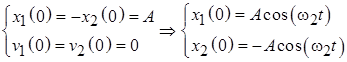 (6.6)
(6.6)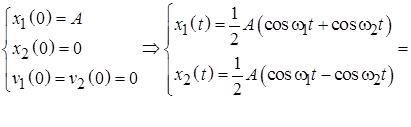
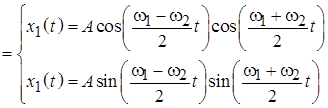 . (6.7)
. (6.7)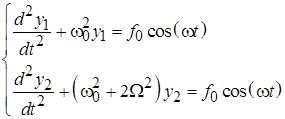
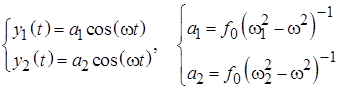 . (6.8)
. (6.8)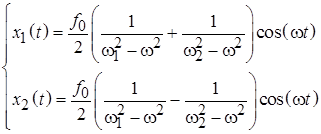 (6.9)
(6.9)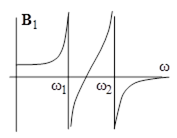
 (1.1)
(1.1)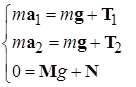 .
.