
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон сохранения механической энергии в потенциальных системах
Полная кинетическая энергия системы материальных точек может быть разделена на кинетическую энергию движения системы как целого и кинетическую энергию движения относительно центра масс («внутреннюю кинетическую энергию движения частиц системы»): Скорость изменения полной кинетической энергии системы определяется мощностью всех сил, действующих на все элементы системы: а само изменение полной кинетической энергии равно суммарной работе всех действующих в системе сил: Доказательства теорем (1.16) и (1.17) об изменении полной кинетической энергии непосредственно вытекают из ранее доказанных теорем о кинетической энергии материальной точки (см. (6.24) из [5]). Силы, входящие в теоремы (1.16) и (1.17), могут быть разделены на внешние (F) и внутренние (f), на потенциальные и непотенциальные:
Для перехода к описанию систем материальных точек на энергетическом языке необходимо введение нового понятия потенциальной энергии системы.
Как правило, нулевое значение потенциальной энергии приписывается конфигурации системы, соответствующей удалению всех элементов системы на бесконечность, где все элементы размещаются на бесконечном расстояниях друг от друга. Совершаемая при этом работа потенциальных сил может быть разделена на два слагаемых: работу сил внешних по отношению к системе и внутренних. Последнее позволяет разделить полную потенциальную энергию на две части, связанные с взаимодействиями системы с внешними объектами и взаимодействиями ее частей друг с другом:
Полную механическую энергию (1.20) удобно разделить на механическую энергию системы как целого (сумма кинетической энергии движения центра масс и потенциальных энергий взаимодействия элементов системы с внешними для нее объектами) и внутреннюю энергию системы (сумма кинетической энергии движения частиц системы относительно ее центра масс и потенциальных энергий их взаимодействий друг с другом: Описание процессов, связанных с изменением внутренней энергии, осуществляется в рамках курсов термодинамики и статистической физики. Скорость изменения полной механической энергии системы материальных точек определяется суммарной мощностью непотенциальных сил, действующих в системе. Изменение механической энергии системы равно работе всех (внешних и внутренних) непотенциальных сил:
В практике решения физических задач наиболее полезными оказываются теоремы (1.16), (1.17), (1.21), (1.22) и (1.23)
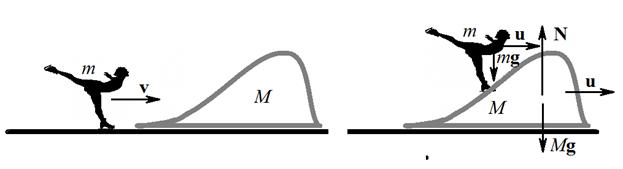
Пример 1.3. Использование законов сохранения в случае невозможности интегрирования уравнения движения. На гладкой ледяной поверхности покоится ледяная глыба массой M, способная скользить без трения. К пологому склону глыбы с начальной скоростью v подъезжает фигуристка массой m, мягко (без удара) переходит на ледяной склон и продолжает движение по нему вверх, по инерции (не отталкиваясь от льда). На какую максимальную высоту заедет фигуристка прежде, чем начнет скатываться вниз?
Рис. 1.4. К задаче на расчет максимальной высоты подъема на скользкий склон
Решение. Данная задача не может быть решена непосредственным интегрированием уравнения движения, поскольку профиль склона не задан и вычисление сил, возникающих между фигуристкой и поверхностью ледяной глыбы невозможно. Однако, отсутствие диссипативных сил позволяет использовать закон сохранения механической энергии (1.23) для двух состояний системы «фигуристка + ледяная глыба»: 1) фигуристка подъезжает к склону и 2) фигуристка достигла наивысшей точки подъема:
В приведенном равенстве учитывается достаточно очевидные факты неизбежного скольжения ледяной глыбы по скользкой горизонтальной поверхности из-за давления не нее фигуристки, катящийся верх по склону, и равенства скоростей глыбы и фигуристки в момент ее остановки относительно склона в точке наивысшего подъема. Наличие двух неизвестных (u и h) требует добавления еще одного уравнения. Закон сохранения импульса, строго говоря, не может быть использован из-за того, что рассматриваемая система не является замкнутой (наличие силы тяжести и реакции опоры со стороны поверхности водоема). Однако, в результате проецирования на горизонтальное направление векторного равенства, выражающего теорему о скорости изменения импульса системы (1.6):
легко убедиться в том, что в рассматриваемом случае остается неизменной во времени проекция суммарного импульса на горизонтальную ось:
Исключение из двух полученных равенств общей скорости фигуристки и опоры в момент достижения наивысшей точки подъема позволяет найти искомую высоту:
Вопросы и задачи для самостоятельной работы 1. Груз массой m, удерживаемый невесомой веревкой с начальной длиной L, вращается, скользя по очень гладкой горизонтальной плоскости. Через проделанное в плоскости небольшое отверстие у неподвижного конца веревки ее (веревку) начинают втягивать в постоянной скоростью v. Найти зависимости от времени координат груза, его угловой и линейной скорости. 2. Пушка стреляет ядром, вылетающим с начальной скоростью V 0 под углом α к горизонту. В верхней точке траектории ядро взрывается, распадаясь на два равных друг ругу осколка, один из которых возвращается в пушку по траектории первой стадии полета. Где упадет второй осколок ядра? 3. N одинаковых солдат массой m каждый стоят на неподвижной платформе массой M. Все солдаты могут бежать по платформе с одинаковой скоростью u. В каком случае платформа приобретет большую скорость: при одновременном или поочередном спрыгивании солдат? 4. Первоначально покоившийся небольшой мешок с песком массой M начинает соскальзывать с высоты H по наклонной плоскости, составляющий угол α c горизонтом. При прохождении через точку перехода склона в горизонтальную плоскость скользящий мешок испытывает удар. На каком расстоянии от точки перехода на горизонтальную поверхность остановится мешок, если коэффициент его трения о поверхности одинаков и равен μ? 5. Доска массой M покоится на горизонтальной поверхности, коэффициент трения о которую равен μ1. На поверхности доски неподвижно лежит брусок массой m. Коэффициент трения бруска и доску равен μ2. С какой горизонтальной силой нужно потянуть доску для того, что бы брусок начал проскальзывать относительно поверхности доски?
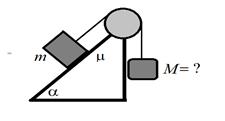
6. На неподвижном клине с углом при основании α размещены два груза, соединенные невесомой нерастяжимой нитью, перекинутой через идеальный невесомый блок (рис. 7.5). Коэффициент трения груза массой m о поверхность клина равен μ. При каких значениях массы М система будет неподвижна? 7. Очень Хорошая Девочка массой m неподвижно сидит на составляющем угол α с горизонталью склоне льдины массой M (рис.7.5). Льдина покоится на ровной горизонтальной поверхности замерзшего водоема. Коэффициент трения льдины о ее горизонтальную опору равен μ1. Очень Невоспитанный Мальчик пытается сдвинуть льдину с места, толкая ее с горизонтальной силой F а) в направлении наклона склона, б) в направлении, противоположном направлению наклонного склона, в) перпендикулярно склону. Каким должен быть коэффициенты трения девочки о лед для того, что бы она смогла усидеть на склоне при условии ускоренного перемещения льдины?
Рис. 1.5. К условиям задач для самостоятельной работы 2. Примеры движения простых систем При решении задач о движении систем материальных точек удобно использовать системы отсчета, связанные с центами масс систем. Задача двух тел Переход в систему центра масс при анализе движения системы из двух взаимодействующих тел позволяет свести задачу к описанию движения одной частицы с приведенной массой. Система уравнений движения двух взаимодействующих между собой тел, не испытывающих воздействие внешних сил имеет вид: Переход от традиционной системы (2.1) к уравнениям в системе отсчета, связанной с центром масс, осуществляется с помощью следующих равенств: В введенной согласно (2.2) системе уравнение движения приобретает вид который путем введения приведенной массы μ приводится к форме, аналогичный уравнению движения одной частицы: Пример. Двойная звезда. Численное моделирование показывает, что компоненты двойной звезды, совершая периодическое движение вокруг общего центра масс, всегда удалены от него на расстояния, обратно пропорциональные их массам. В случае одинаковых масс (рис. 2.1) обе компоненты движутся по одинаковым пересекающимся траекториям. Если массы компонент дойной звезды различны, то более массивная движется по траектории с меньшими характерными размерами. В этом случае более компактная траектория может быть как вложена в большую (рис. 2.2), так и может с ней пересекаться. Во всех случаях компактные компоненты двойной звезды никогда не сталкиваются друг с другом из-за того, то всегда располагаются на различных концах отрезка переменной длины, походящего через их общий центр масс. Методы аналитического решения уравнения движения (2.3) в случае гравитационного взаимодействия тел (см. (4.21) из [5]) будут рассмотрены в разделе, посвященном закону всемирного тяготения.
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-19; просмотров: 115; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.191.22 (0.021 с.) |

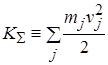
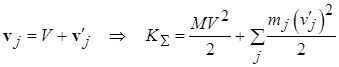 . (1.15)
. (1.15) , (1.16)
, (1.16)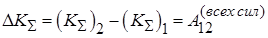 . (1.17)
. (1.17)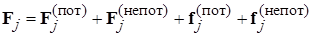 . (1.18)
. (1.18)
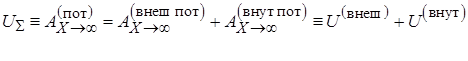 . (1.19)
. (1.19)
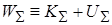 . (1.20)
. (1.20)
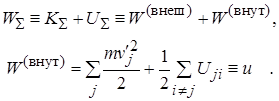
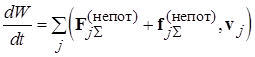 . (1.21)
. (1.21) . (1.22)
. (1.22)
 . (1.23)
. (1.23)
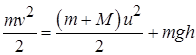 .
.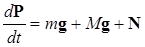 ,
,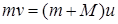 .
. .
.

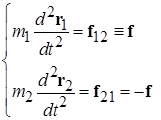 . (2.1)
. (2.1) (2.2)
(2.2)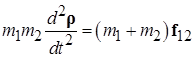 ,
, 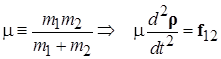 . (2.3)
. (2.3)


