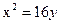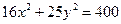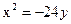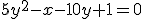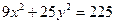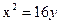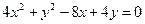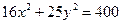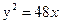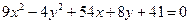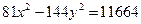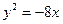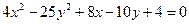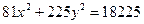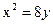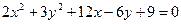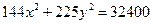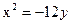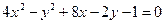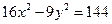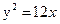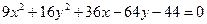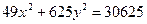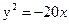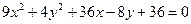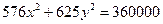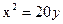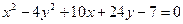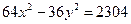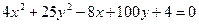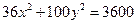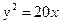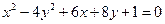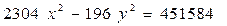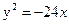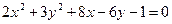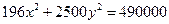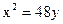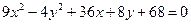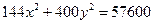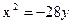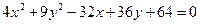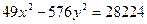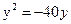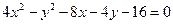Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Краткие теоретические сведения.Содержание книги Поиск на нашем сайте
Алгебраической кривой второго порядка называется кривая, уравнение которой в декартовой системе координат имеет вид: Аx2 + 2Вxy + Сy2 + 2Dx + 2Еy + F = 0, где не все коэффициенты А, В и С равны одновременно нулю. Эллипс – геометрическое множество точек плоскости, сумма расстояний от которых до двух точек F1 и F2, называемых фокусами, есть величина постоянная 2a, большая, чем расстояние между фокусами 2c:
Если а>b, то фокусы находятся на оси ОХ на расстоянии Число
Гипербола – геометрическое множество точек плоскости, модуль разности расстояний от которых до двух точек F1 и F2, называемых фокусами, есть величина постоянная 2a, меньшая, чем расстояние между фокусами 2c: Гипербола, заданная каноническим уравнением Параметр а называется вещественной полуосью, b – мнимой полуосью. Число Прямые Гипербола, заданная каноническим уравнением В этом случае параметр b называется вещественной полуосью, a – мнимой полуосью. Эксцентриситет вычисляется по формуле
Если р>0, то в обоих случаях ветви параболы обращены в положительную сторону соответствующей оси, а если р<0 – в отрицательную сторону.
Кривые 2-го порядка со смещенными центрами (вершинами)
Для того, чтобы понять, как именно расположена кривая относительно системы координат и каковы ее параметры, уравнение можно преобразовать способом выделения полных квадратов. После этого уравнение примет вид одного из невырожденных уравнений кривой 2-го порядка со смещенным центром: 1) 2) 3) это параболы с вершиной
Пример 1. Написать каноническое уравнение гиперболы, зная, что расстояние между фокусами равно 24, а между вершинами 16. Решение:
а) по условию
Получим уравнение гиперболы Пример 2. Найти полуоси, координаты фокусов, эксцентриситет, уравнения асимптот гиперболы 9x2-16y2=144. Сделать чертеж. Решение. Приведем данное уравнение к каноническому виду (разделив его на 144):
Пример 3. Определить вид кривой, найти ее центр (вершину) и вычислить основные параметры: а) б) а) Преобразуем уравнение. Объединяем члены с одной переменной, коэффициент при квадрате выносим за скобку:
Дополняем выражения в скобках до полных квадратов:
Лишние свободные члены из скобок убираем и переносим вправо, тождественно преобразуя левую часть:
Делим на (-36): получили уравнение гиперболы с центром Действительная ось гиперболы параллельна оси Фокусы:
Асимптоты гиперболы:
б) Преобразуем уравнение. Так как в данном уравнении только одна переменная имеет степень, равную 2, то это уравнение задает параболу. Тогда в левой части уравнения оставляем переменную второй степени, остальные слагаемые переносим в правую часть, выносим коэффициент перед квадратом за скобку и выделяем в левой части полный квадрат, лишний свободный член переносим вправо, выносим в правой части коэффициент перед переменной за скобку и делим обе части на коэффициент перед скобкой в левой части уравнения.
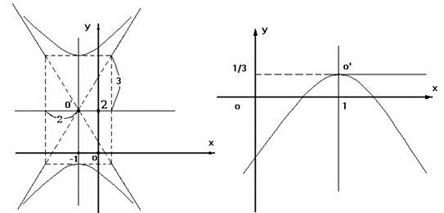
Вершина параболы Ось x = 1 – параллельна оси Ветви направлены вниз, параметр Фокус: Директриса:
Задание для совместного решения. 1. Составить уравнение эллипса, если известно, что разница между его большой и малой полуосью составляет 18, а фокусы находятся на расстоянии 24 от центра. Ответ: 2. Привести уравнение кривой второго порядка к каноническому виду, вычислить все параметры кривой (вершины, фокусы, эксцентриситеты, асимптоты, директрису), выполнить чертеж а) б) в) Ответ: а) б) в)
Задания для самостоятельного решения. Задача №1. Составить уравнение кривой второго порядка, удовлетворяющей следующим условиям.
Задача №2. Привести уравнения кривых второго порядка к каноническому виду, вычислить все параметры кривой (вершины, фокусы, эксцентриситеты, асимптоты, директрису), выполнить чертеж.
Занятие 5*. Уравнение плоскости
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-17; просмотров: 383; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.160.135 (0.011 с.) |

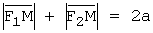 .
.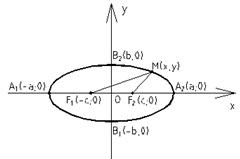 Эллипс, заданный каноническим уравнением
Эллипс, заданный каноническим уравнением 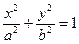 симметричен относительно осей координат. Параметры а и b называются полуосями эллипса (большой и малой соответственно).
симметричен относительно осей координат. Параметры а и b называются полуосями эллипса (большой и малой соответственно).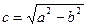 от центра эллипса О.
от центра эллипса О.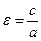 называется эксцентриситетом эллипса и является мерой его «сплюснутости» (при
называется эксцентриситетом эллипса и является мерой его «сплюснутости» (при 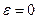 эллипс является окружностью, а при
эллипс является окружностью, а при 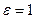 он вырождается в отрезок длиною 2a).
он вырождается в отрезок длиною 2a).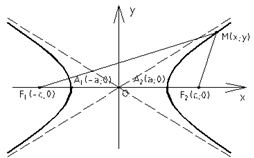 Если а<b, то фокусы находятся на оси ОY и
Если а<b, то фокусы находятся на оси ОY и 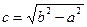 ,
, 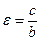 .
.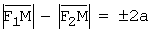 .
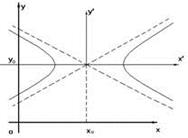
.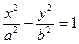 симметрична относительно осей координат. Она пересекает ось ОХ в точках
симметрична относительно осей координат. Она пересекает ось ОХ в точках 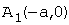 и
и 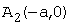 - вершинах гиперболы, и не пересекает оси ОY.
- вершинах гиперболы, и не пересекает оси ОY.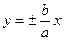 называются асимптотами гиперболы.
называются асимптотами гиперболы.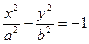 называется сопряжённой (имеет те же асимптоты). Её фокусы расположены на оси OY. Она пересекает ось ОY в точках
называется сопряжённой (имеет те же асимптоты). Её фокусы расположены на оси OY. Она пересекает ось ОY в точках 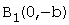 и
и 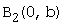 - вершинах гиперболы, и не пересекает оси ОX.
- вершинах гиперболы, и не пересекает оси ОX.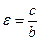 .
.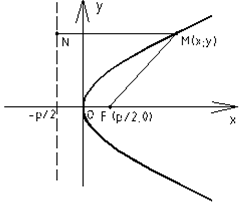 Парабола – множество точек плоскости, равноудаленных от данной точки F, называемой фокусом, и данной прямой, называемой директрисой:
Парабола – множество точек плоскости, равноудаленных от данной точки F, называемой фокусом, и данной прямой, называемой директрисой:  .
.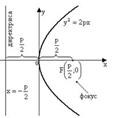 Уравнение:
Уравнение: 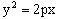 (1) Ось симметрии параболы – ось Ox
(1) Ось симметрии параболы – ось Ox
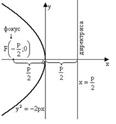 Уравнение:
Уравнение: 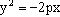 (2) Ось симметрии параболы – ось Ox
(2) Ось симметрии параболы – ось Ox
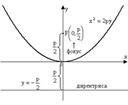 Уравнение:
Уравнение: 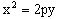 (3) Ось симметрии параболы – ось Oy
(3) Ось симметрии параболы – ось Oy
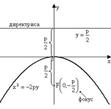 Уравнение:
Уравнение: 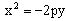 (4) Ось симметрии параболы – ось Oy
(4) Ось симметрии параболы – ось Oy
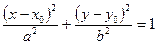 это уравнение эллипса с центром
это уравнение эллипса с центром 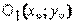 и осями, параллельными осям
и осями, параллельными осям  и
и 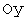 ;
;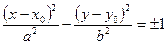 и
и 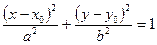 и, эти уравнения определяют гиперболы с центром
и, эти уравнения определяют гиперболы с центром  и осями, параллельными координатным;
и осями, параллельными координатным;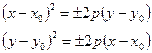
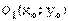 и осью, параллельной одной из координатных.
и осью, параллельной одной из координатных.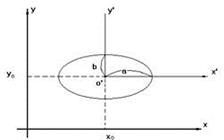
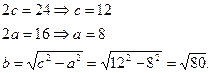
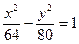
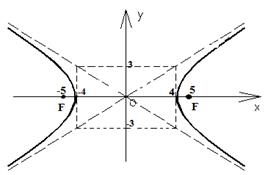
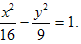 Отсюда следует, что a2=16, b2=9. Следовательно, a=4 -действительная полуось, b=3 - мнимая полуось. Тогда
Отсюда следует, что a2=16, b2=9. Следовательно, a=4 -действительная полуось, b=3 - мнимая полуось. Тогда 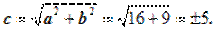 Значит, фокусы имеют координаты F1(-5,0), F2(5,0). Находим эксцентриситет
Значит, фокусы имеют координаты F1(-5,0), F2(5,0). Находим эксцентриситет 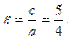
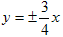 .
.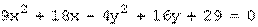
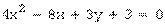
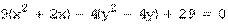
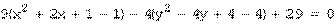
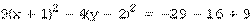 или
или 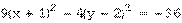
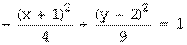
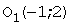 , полуосями a=2, b=3, осями параллельными координатным.
, полуосями a=2, b=3, осями параллельными координатным.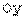 : x= -1, мнимая – параллельна оси
: x= -1, мнимая – параллельна оси 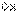 : y=2;
: y=2; 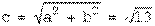 .
.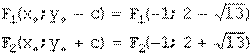
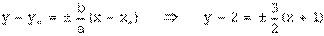
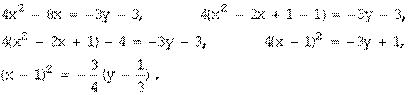
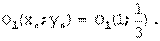
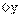 .
.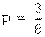 .
.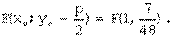
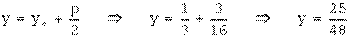 .
.
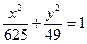
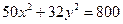 ;
;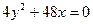 ;
;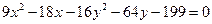 .
.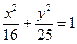 - уравнение эллипса;
- уравнение эллипса;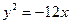 - уравнение параболы;
- уравнение параболы;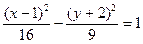 - уравнение гиперболы.
- уравнение гиперболы.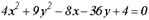
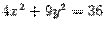
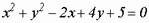
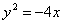
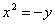
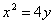
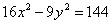
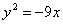
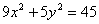 .
.
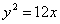
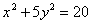
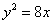
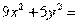 45
45
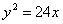
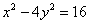
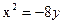
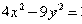 72
72
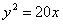
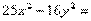 400
400
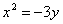
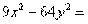 576
576
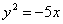
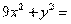 18
18