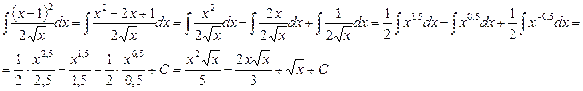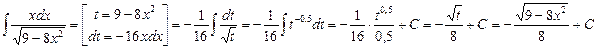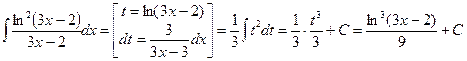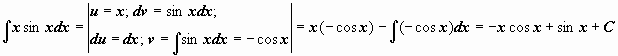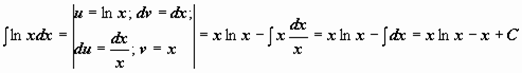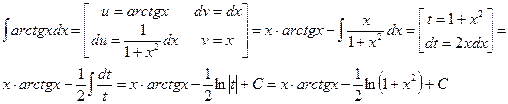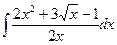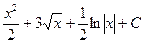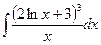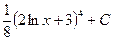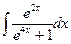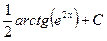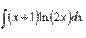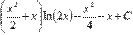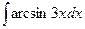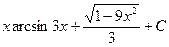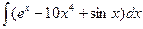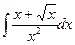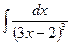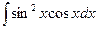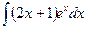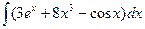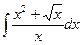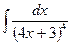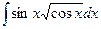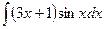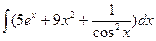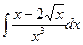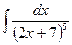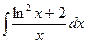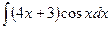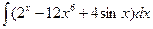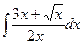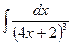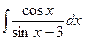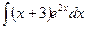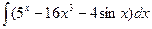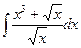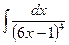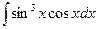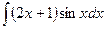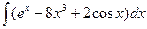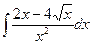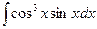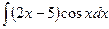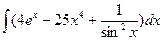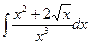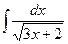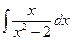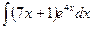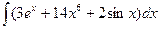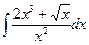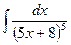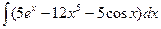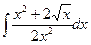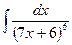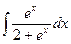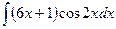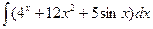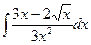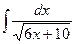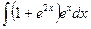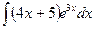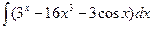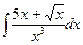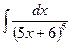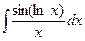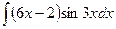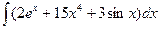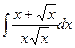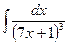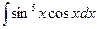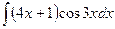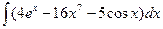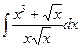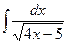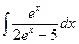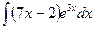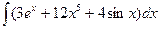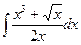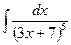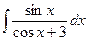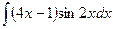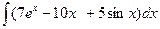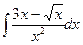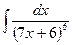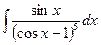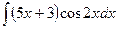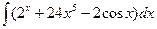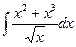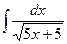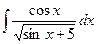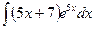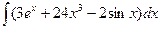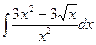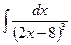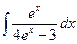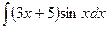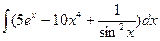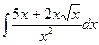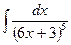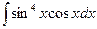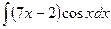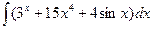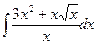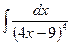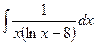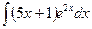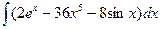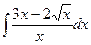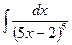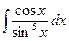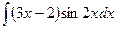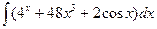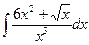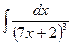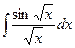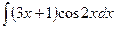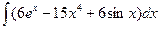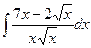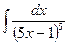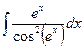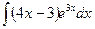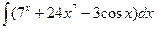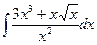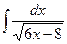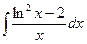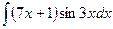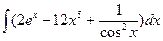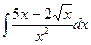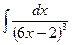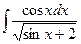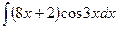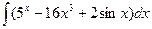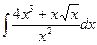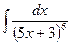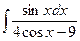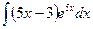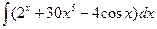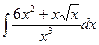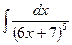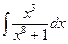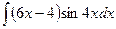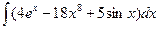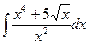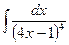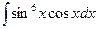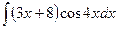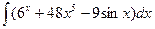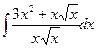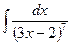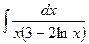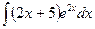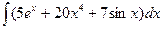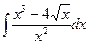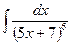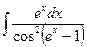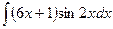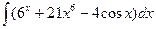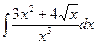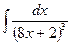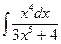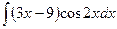Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Краткие теоретические сведения.Комплексным числом z называется выражение Числа
Таким образом, на оси ОХ располагаются действительные числа, а на оси ОY – чисто мнимые. С помощью подобного геометрического представления можно представлять числа в так называемой тригонометрической форме. Из геометрических соображений видно, что
и таблицы:
Основные действия с комплексными числами вытекают из действий с многочленами. 1) Сложение и вычитание.
2) Умножение.
В тригонометрической форме:
В случае комплексно-сопряженных чисел: 3) Деление.
В тригонометрической форме: 4) Возведение в степень.
5) Извлечение корня из комплексного числа.
Таким образом, корень n – ой степени из комплексного числа имеет n различных значений. Если представить комплексное число в тригонометрической форме:
Пример 1. а) (2 + 3i) + (5 + i) = (2 + 5) + (3 + 1)i = 7 + 4i; б) (5 – 8i) – (2 + 3i) = (3 – 2) + (– 8 – 3)i = 1 – 11i; в) (– 1 + 3i)(2 + 5i) = – 2 – 5i + 6i + 15i2 = – 2 – 5i + 6i – 15 = – 17 + i; г) д) Для числа Число
Тогда Для нахождения
е) Для числа z из предыдущего примера вычислить
Задания для совместного решения: Выполнить с данными комплексными числами а) Ответ: а) 3-i,б) -8+9i в) -4 - Задания для самостоятельного решения Выполнить с данными комплексными числами следующие действия: а)
Занятие 7. Неопределенный интеграл Краткие теоретические сведения. Таблица неопределенных интегралов.
Свойства неопределенного интеграла.
Замена переменной в неопределенном интеграле:
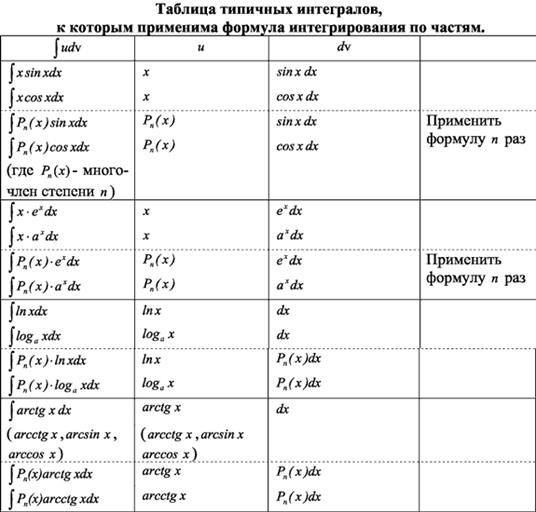
Интегрирование по частям в неопределенном интеграле:
В таблице приведены типичные интегралы, которые интегрируются по частям и способы разбиения этих интегралов на части. Пример 1. Найти неопределенные интегралы:
Задания для совместного решения.
Задания для самостоятельного решения.
Занятие 8. Определенный интеграл
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-17; просмотров: 122; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.143.181 (0.006 с.) |
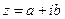 , где a и b – действительные числа, i – мнимая единица, которая определяется соотношением:
, где a и b – действительные числа, i – мнимая единица, которая определяется соотношением:  При этом число a называется действительной частью числа z (a = Re z), а b – мнимой частью (b = Im z). Если a = Re z =0, то число z будет чисто мнимым, если b = Im z = 0, то число z будет действительным.
При этом число a называется действительной частью числа z (a = Re z), а b – мнимой частью (b = Im z). Если a = Re z =0, то число z будет чисто мнимым, если b = Im z = 0, то число z будет действительным.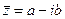 называются комплексно – сопряженными.
называются комплексно – сопряженными.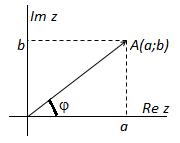 Если любое действительное число может быть геометрически представлено в виде точки на числовой прямой, то комплексное число представляется точкой на плоскости, координатами которой будут соответственно действительная и мнимая части комплексного числа. При этом горизонтальная ось будет являться действительной числовой осью, а вертикальная - мнимой осью.
Если любое действительное число может быть геометрически представлено в виде точки на числовой прямой, то комплексное число представляется точкой на плоскости, координатами которой будут соответственно действительная и мнимая части комплексного числа. При этом горизонтальная ось будет являться действительной числовой осью, а вертикальная - мнимой осью.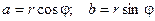 . Тогда комплексное число можно представить в виде:
. Тогда комплексное число можно представить в виде: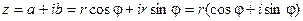 . Такая форма записи называется тригонометрической формой записи комплексного числа. При этом величина r называется модулем комплексного числа, а угол наклона j - аргументом комплексного числа:
. Такая форма записи называется тригонометрической формой записи комплексного числа. При этом величина r называется модулем комплексного числа, а угол наклона j - аргументом комплексного числа: 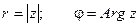 ,
, 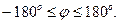 Из геометрических соображений видно:
Из геометрических соображений видно: 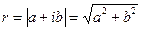 . Для числа z = 0 аргумент не определён. В остальных случаях аргумент может быть найден из соотношения:
. Для числа z = 0 аргумент не определён. В остальных случаях аргумент может быть найден из соотношения: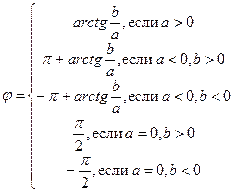
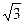
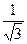
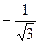

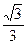
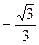

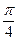
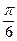
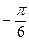
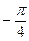
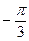
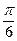
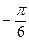
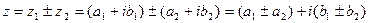
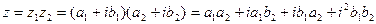
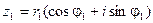 ,
, 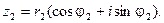
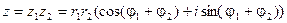
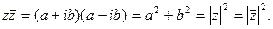
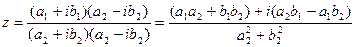
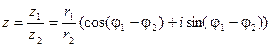
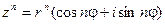 , где n – целое положительное число. Это выражение называется формулой Муавра.
, где n – целое положительное число. Это выражение называется формулой Муавра.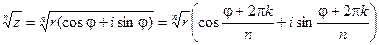
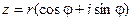 и воспользоваться формулой Эйлера:
и воспользоваться формулой Эйлера: 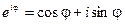 , то получим
, то получим 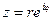 . Полученное равенство есть показательная форма комплексного числа.
. Полученное равенство есть показательная форма комплексного числа.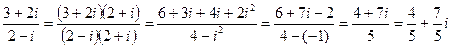
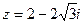 найти тригонометрическую форму и вычислить z20
найти тригонометрическую форму и вычислить z20 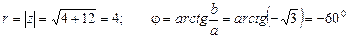
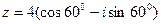 .
. воспользуемся формулой Муавра.
воспользуемся формулой Муавра.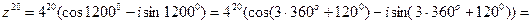
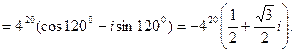
 .
.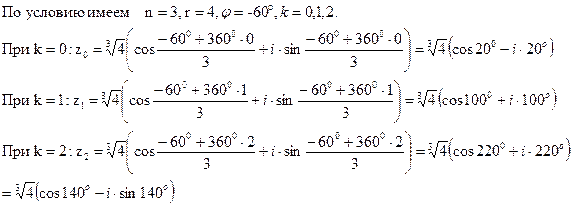
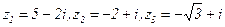 следующие действия:
следующие действия: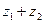 б)
б) 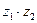 в)
в) 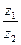 г) Число
г) Число 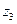 представить в тригонометрической и показательной форме и найти
представить в тригонометрической и показательной форме и найти 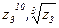 .
.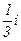 г) z3=2(cos1500+i sin 1500), z310=1024(cos 600+i sin 600),
г) z3=2(cos1500+i sin 1500), z310=1024(cos 600+i sin 600), 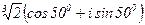 ,
, 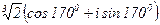 ,
, 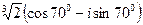 .
.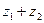 б)
б) 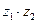 в)
в) 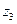 представить в тригонометрической и показательной форме и найти
представить в тригонометрической и показательной форме и найти 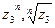
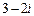
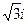
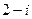
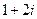
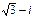
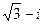
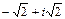
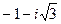
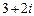
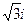
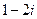
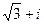
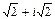
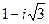
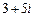
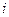
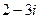
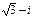
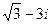
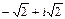
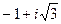
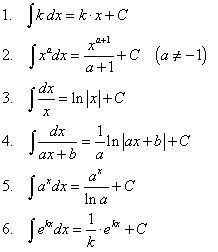
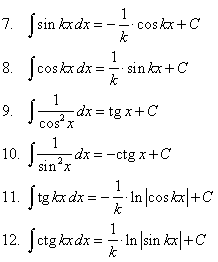
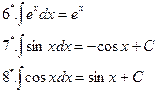
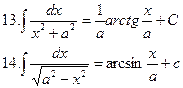
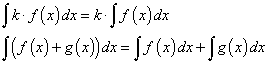
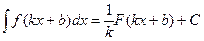
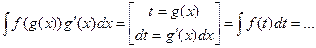
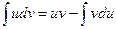 .
.