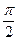Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Краткие теоретические сведения.Стр 1 из 8Следующая ⇒
Задания для совместного решения. №1 Вычислить матрицу D = 3A + 2B, где
№2. Даны матрицы А и В. Найти матрицу E = AT × A + B
№3. Вычислить определители матриц:
Задания для самостоятельного решения:
№1.Даны матрицы: Найти матрицу, равную значению выражения.
№2.Вычислить определители матрицы а) по любой строке или столбцу б) по правилу треугольника
Занятие 2. Решение систем линейных уравнений Краткие теоретические сведения. Матричный метод решения систем линейных уравнений. Пусть дана система уравнений:
Составляются матрицы: A = Решением системы является матрица-столбец X = Х = А-1 ×В.
Пример 1. Решить систему уравнений:
Х = Найдем обратную матрицу А-1. D = det A = А11 = (-1)1+1 А12 = (-1)1+2 А13 =(-1)1+3 A-1 = Х= Решение системы: x =1; y = 2; z = 3. Метод Крамера. Теорема. Система из n уравнений с n неизвестными xi = Di/D, где D = det A, а Di – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов bi. Di = Пример 2. Найти решение системы уравнений: D = D1 =
D2 = D3 = Метод Гаусса. Рассмотрим систему линейных уравнений: Разделим обе части 1–го уравнения на a11 ¹ 0, затем: 1) умножим на а21 и вычтем из второго уравнения 2) умножим на а31 и вычтем из третьего уравнения и т.д. Получим:
dij = aij – ai1d1j i = 2, 3, …, n; j = 2, 3, …, n+1. Далее повторяем эти же действия для второго уравнения системы, потом – для третьего и т.д. Пример 3. Решить систему линейных уравнений методом Гаусса. Составим расширенную матрицу системы. А* = Таким образом, исходная система может быть представлена в виде:
Задания для совместного решения. Решить данную систему а) методом обратной матрицы б) методом Крамера в) методом Гаусса
Задания для самостоятельного решения Решить данную систему а) методом обратной матрицы б) методом Крамера в) методом Гаусса
Занятие 3. Векторы Задания для совместного решения. Даны векторы Вычислить: а) вектор б) модули векторов в) г) угол между векторами д) проекцию вектора е) векторное произведение ж) площадь параллелограмма и площадь треугольника, построенного на векторах з) смешанное произведение векторов и) объем параллелепипеда и объем тетраэдра, построенных на векторах Ответ: а) Задания для самостоятельного решения. Для данных векторов а) вектор б) модули векторов в) г) угол между векторами д) проекцию вектора е) векторное произведение ж) площадь параллелограмма и площадь треугольника, построенного на векторах з) смешанное произведение векторов и) объем параллелепипеда и объем тетраэдра, построенных на векторах
Занятие 4. Прямая линия на плоскости Задание для совместного решения. 1. Составить уравнение эллипса, если известно, что разница между его большой и малой полуосью составляет 18, а фокусы находятся на расстоянии 24 от центра. Ответ: 2. Привести уравнение кривой второго порядка к каноническому виду, вычислить все параметры кривой (вершины, фокусы, эксцентриситеты, асимптоты, директрису), выполнить чертеж а) б) в) Ответ: а) б) в)
Задания для самостоятельного решения. Задача №1. Составить уравнение кривой второго порядка, удовлетворяющей следующим условиям.
Задача №2. Привести уравнения кривых второго порядка к каноническому виду, вычислить все параметры кривой (вершины, фокусы, эксцентриситеты, асимптоты, директрису), выполнить чертеж.
Занятие 5*. Уравнение плоскости Задания для совместного решения. 1. Вычислить определенные интегралы: а) б) в) 2. Определить площадь фигуры, ограниченной параболой y = x2 + 1 и прямой x + y = 3. (Ответ: 4,5). 3. Вычислить объем тела, полученного вращением вокруг оси Ox фигуры, ограниченной параболами y = x2 и x = y2. (Ответ: 0,3π)
Задания для самостоятельного решения.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
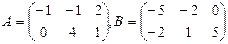 Ответ:
Ответ: 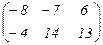
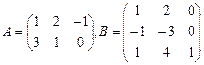 Ответ:
Ответ: 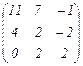

 Ответ: 13; -6
Ответ: 13; -6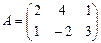 В=
В= 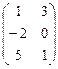 С=
С= 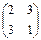
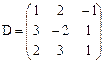
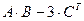
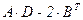
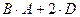
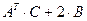
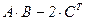
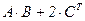
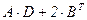
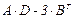
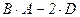
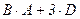
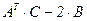
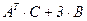
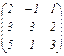
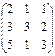
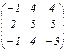
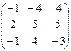
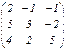
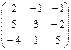
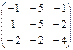
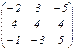
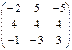
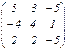
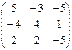
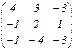
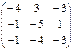
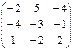
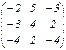
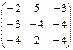
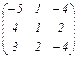
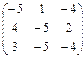
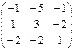
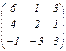
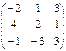
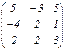
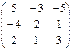
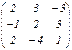
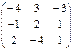
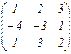
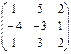
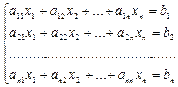
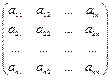 ; B =
; B = 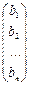 ;
;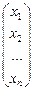 , определяемая по формуле:
, определяемая по формуле: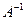 - матрица, обратная матрице А. Обратная матрица может быть определена различными способами. Один из них – с помощью алгебраических дополнений.
- матрица, обратная матрице А. Обратная матрица может быть определена различными способами. Один из них – с помощью алгебраических дополнений.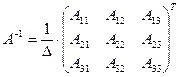 .
.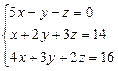
 , B =
, B = 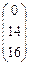 , A =
, A = 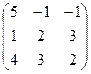
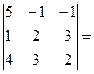 5(4-9) + 1(2 – 12) – 1(3 – 8) = -25 – 10 +5 = -30.
5(4-9) + 1(2 – 12) – 1(3 – 8) = -25 – 10 +5 = -30.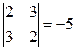 А21 = (-1)2+1
А21 = (-1)2+1 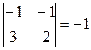 А31 = (-1)3+1
А31 = (-1)3+1 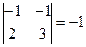
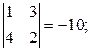 А22 = (-1)2+2
А22 = (-1)2+2 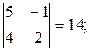 А32 = (-1)3+2
А32 = (-1)3+2 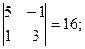
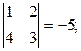 А23 = (-1)2+3
А23 = (-1)2+3 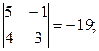 А33 = (-1)3+3
А33 = (-1)3+3 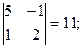
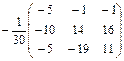 ;
;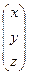 = А-1В =
= А-1В = 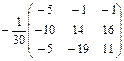 ×
× 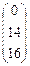 =
= 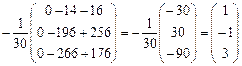 .
.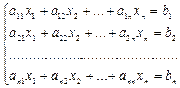 в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:
в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам: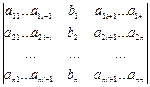
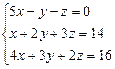
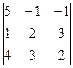 = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
= 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;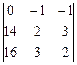 = (28 – 48) – (42 – 32) = -20 – 10 = -30. x1 = D1/D = 1;
= (28 – 48) – (42 – 32) = -20 – 10 = -30. x1 = D1/D = 1;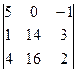 = 5(28 – 48) – (16 – 56) = -100 + 40 = -60. x2 = D2/D = 2;
= 5(28 – 48) – (16 – 56) = -100 + 40 = -60. x2 = D2/D = 2;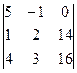 = 5(32 – 42) + (16 – 56) = -50 – 40 = -90. x3 = D3/D = 3.
= 5(32 – 42) + (16 – 56) = -50 – 40 = -90. x3 = D3/D = 3.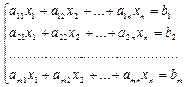
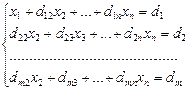 , где d1j = a1j/a11, j = 2, 3, …, n+1.
, где d1j = a1j/a11, j = 2, 3, …, n+1.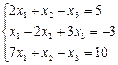
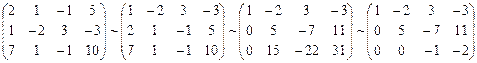
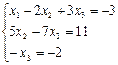 , откуда получаем: x3 = 2; x2 = 5; x1 = 1.
, откуда получаем: x3 = 2; x2 = 5; x1 = 1.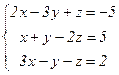 Ответ: (1; 2; -1)
Ответ: (1; 2; -1)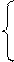
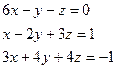
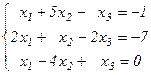
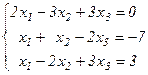
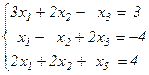
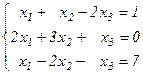
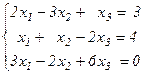
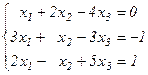
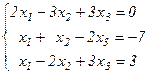
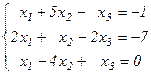
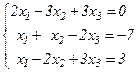
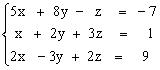
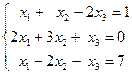
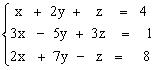
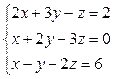
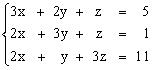
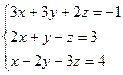
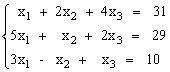
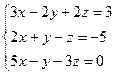
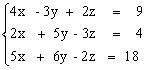

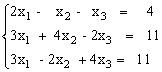
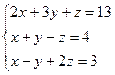
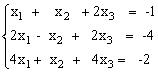
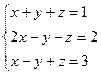
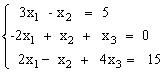
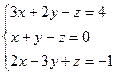
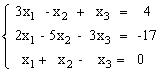
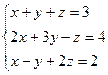
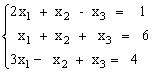
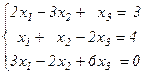
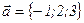 ,
, 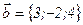 ,
, 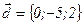
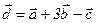
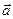 и
и 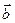
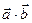
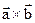
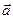 и
и 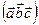 . Являются ли векторы компланарными?
. Являются ли векторы компланарными?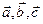
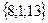 б)
б) 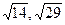 в) 5 г) arccos
в) 5 г) arccos 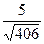 д)
д) 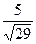 е)
е) 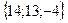 ж)
ж) 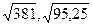 з) -73, не являются и)
з) -73, не являются и) 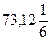
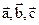 вычислить:
вычислить: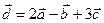
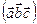 . Являются ли векторы компланарными?
. Являются ли векторы компланарными?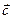
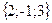
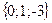
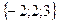
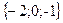
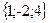
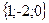
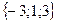
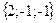
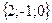
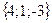
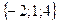
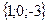
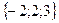
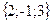
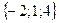
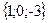
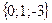
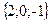
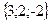
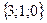
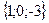
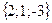
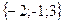
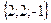
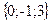
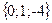
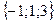
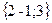
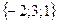
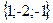
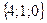
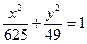
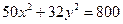 ;
;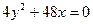 ;
;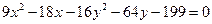 .
.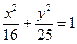 - уравнение эллипса;
- уравнение эллипса;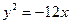 - уравнение параболы;
- уравнение параболы;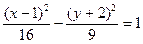 - уравнение гиперболы.
- уравнение гиперболы.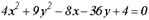
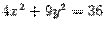
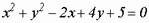
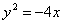
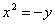
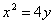
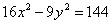
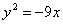
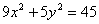 .
.
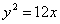
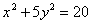
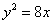
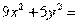 45
45
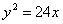
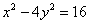
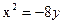
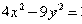 72
72
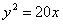
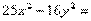 400
400
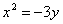
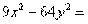 576
576
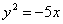
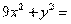 18
18
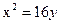
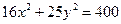
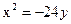
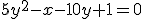
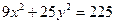
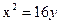
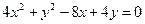
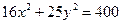
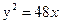
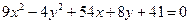
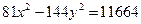
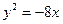
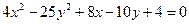
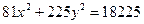
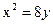
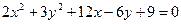
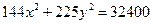
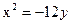
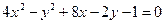
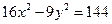
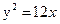
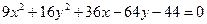
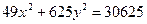
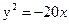
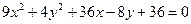
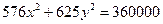
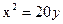
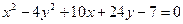
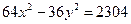
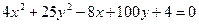
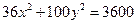
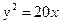
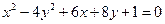
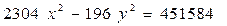
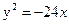
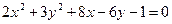
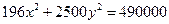
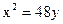
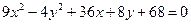
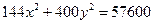
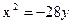
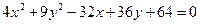
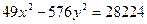
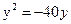
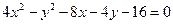
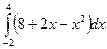 Ответ: 36
Ответ: 36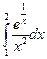 Ответ:
Ответ: 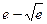
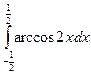 Ответ:
Ответ: