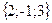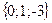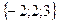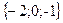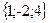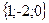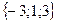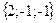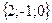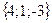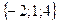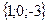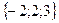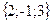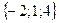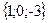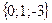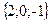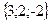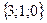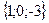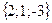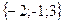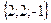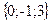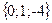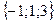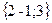Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Краткие теоретические сведенияСодержание книги Поиск на нашем сайте
Длина вектора в координатах определяется как расстояние между точками начала и конца вектора. Если заданы две точки в пространстве А(х1, y1, z1), B(x2, y2, z2), то Пусть заданы векторы в прямоугольной системе координат
Скалярным произведением векторов Если рассматривать векторы Используя полученные равенства, получаем формулу для вычисления угла между векторами:
Проекция вектора
В координатной форме формула для проекции примет вид
Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах Пример: Заданы два вектора в пространстве Решение. Сумма векторов:
Разность векторов:
Косинус угла α между векторами:
Векторное произведение:
Смешанное произведение векторов. Если
- смешанное произведение векторов.
Смешанное произведение Три вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Условие компланарности: Пример 1: Вычислить смешанное произведение векторов Решение:
Задания для совместного решения. Даны векторы Вычислить: а) вектор б) модули векторов в) г) угол между векторами д) проекцию вектора е) векторное произведение ж) площадь параллелограмма и площадь треугольника, построенного на векторах з) смешанное произведение векторов и) объем параллелепипеда и объем тетраэдра, построенных на векторах Ответ: а) Задания для самостоятельного решения. Для данных векторов а) вектор б) модули векторов в) г) угол между векторами д) проекцию вектора е) векторное произведение ж) площадь параллелограмма и площадь треугольника, построенного на векторах з) смешанное произведение векторов и) объем параллелепипеда и объем тетраэдра, построенных на векторах
Занятие 4. Прямая линия на плоскости
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-17; просмотров: 106; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.47.239 (0.008 с.) |

 .
.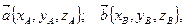 тогда сумма и умножение вектора на число соответствует аналогичной операции с координатами
тогда сумма и умножение вектора на число соответствует аналогичной операции с координатами 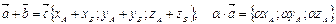
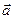 и
и 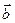 называется число, равное произведению длин этих сторон на косинус угла между ними
называется число, равное произведению длин этих сторон на косинус угла между ними 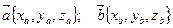 в декартовой прямоугольной системе координат, то
в декартовой прямоугольной системе координат, то 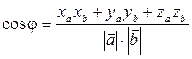 ;
;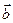 определяется по формуле:
определяется по формуле: .
.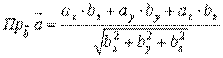 .
. Если заданы векторы
Если заданы векторы 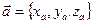 и
и 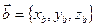 в декартовой прямоугольной системе координат с единичными векторами
в декартовой прямоугольной системе координат с единичными векторами 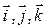 , то векторное произведение – вектор, координаты которого определяются с помощью определителя:
, то векторное произведение – вектор, координаты которого определяются с помощью определителя: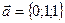 и
и 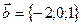 . Найти а) сумму этих векторов б) их разность в) косинус угла между ними г) векторное произведение векторов.
. Найти а) сумму этих векторов б) их разность в) косинус угла между ними г) векторное произведение векторов.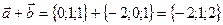
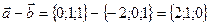
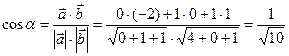 .
.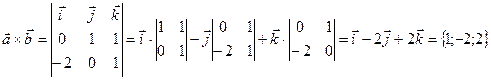
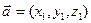 ,
, 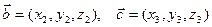 , то
, то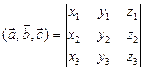
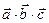 по модулю равно объему параллелепипеда, построенного на векторах
по модулю равно объему параллелепипеда, построенного на векторах 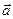 ,
, 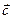 .
.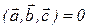
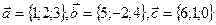
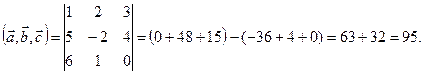
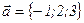 ,
, 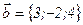 ,
, 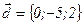
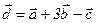
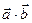
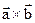
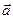 и
и 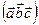 . Являются ли векторы компланарными?
. Являются ли векторы компланарными?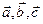
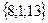 б)
б) 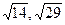 в) 5 г) arccos
в) 5 г) arccos 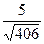 д)
д) 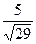 е)
е) 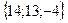 ж)
ж) 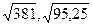 з) -73, не являются и)
з) -73, не являются и) 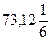
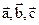 вычислить:
вычислить: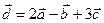
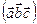 . Являются ли векторы компланарными?
. Являются ли векторы компланарными?