Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Краткие теоретические сведения.
Определение. Любая прямая на плоскости может быть задана уравнением первого порядка Ах + Ву + С = 0, причем постоянные А, В не равны нулю одновременно, т.е. А2 + В2 ¹ 0. Это уравнение первого порядка называют общим уравнением прямой. Вектор Уравнение прямой, проходящей через данную точку Пусть на плоскости заданы две точки M1(x1, y1) и M2(x2, y2), тогда уравнение прямой, проходящей через эти точки:
Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель. Определение. Каждый ненулевой вектор Геометрически направляющий вектор – вектор, параллельный прямой. Уравнение прямой, проходящей через данную точку Если общее уравнение прямой Ах + Ву + С = 0 привести к виду и обозначить Определение. Если заданы две прямые А1х + В1у + С1 = 0 и А2х + В2у + С2 = 0, то острый угол между этими прямыми будет определяться как Две прямые параллельны, если Две прямые перпендикулярны, если Координаты точки пересечения двух прямых находятся как решение системы двух уравнений. Прямая, проходящая через точку М1(х1, у1) и перпендикулярная к прямой Ах + Ву + С = 0 представляется уравнением: Если задана точка М(х0, у0), то расстояние до прямой Ах + Ву + С =0 определяется как Пример 1. Даны вершины треугольника А(0; 1), B(6; 5), C(12; -1). а) Составить уравнения сторон треугольника б) Найти уравнение высоты CD, проведенной из вершины С. в) Найти координаты точки D г) Найти длину высоты CD д) Составить уравнение медианы MN, параллельной стороне АВ е) Вычислить косинус угла А. Решение. а) Находим уравнение стороны АВ:
4x = 6y – 6; 2x – 3y + 3 = 0; Уравнение ВС: Уравнение AC б) Высота CD лежит на прямой, проходящей через точку С, перпендикулярно прямой АВ. Тогда ее уравнение:
в) Координаты точки D находятся как координаты точки пересечения прямых CD и АВ.
г) Длину высоты АВ можно определить как расстояние от точки С до прямой АВ.
д) Уравнение медианы MN составим как уравнение прямой, проходящей через точку М – середину стороны АС, параллельно прямой АВ. Найдем координаты М
е) Косинус угла А вычислим как косинус угла между прямыми АВ и АС.
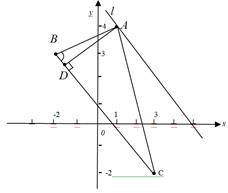
Задание для совместного решения: Даны координаты вершин треугольника а) Уравнения сторон треугольника б) Уравнение высоты АD и ее длину в) Координаты точки D. г) Уравнение прямой, проходящей через точку А, параллельно ВС д) Угол В в градусах (округлить до целого значения) Сделать чертеж. Ответ: а) АВ: б) Задание для самостоятельного решения: Даны координаты вершин треугольника а) Уравнения сторон треугольника б) Уравнение высоты АD и ее длину в) Координаты точки D. г) Уравнение прямой, проходящей через точку А, параллельно ВС д) Угол В в градусах (округлить до целого значения)
Занятие 5. Кривые второго порядка
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-17; просмотров: 81; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.228.88 (0.01 с.) |
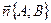 называется нормальным вектором, он перпендикулярен прямой Ах + Ву + С = 0.
называется нормальным вектором, он перпендикулярен прямой Ах + Ву + С = 0.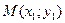 с нормальным вектором
с нормальным вектором 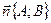 , имеет вид
, имеет вид 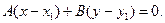
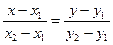
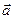 {a1, a2}, координаты которого удовлетворяют условию Аa1 + Вa2 = 0 называется направляющим вектором прямой Ах + Ву + С = 0.
{a1, a2}, координаты которого удовлетворяют условию Аa1 + Вa2 = 0 называется направляющим вектором прямой Ах + Ву + С = 0.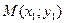 с направляющим вектором
с направляющим вектором  имеет вид:
имеет вид: 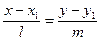 . Уравнение, записанное в таком виде называется каноническим. Путем преобразований оно может быть сведено к общему виду.
. Уравнение, записанное в таком виде называется каноническим. Путем преобразований оно может быть сведено к общему виду.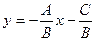
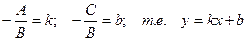 , то полученное уравнение называется уравнением прямой с угловым коэффициентом k.
, то полученное уравнение называется уравнением прямой с угловым коэффициентом k.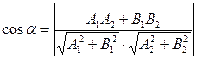 .
.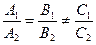 .
.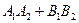 =0.
=0.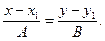 Прямая, проходящая через точку М1(х1, у1) и параллельная к прямой Ах + Ву + С = 0 представляется уравнением:
Прямая, проходящая через точку М1(х1, у1) и параллельная к прямой Ах + Ву + С = 0 представляется уравнением: 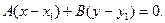
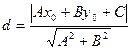 .
.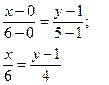 ;
;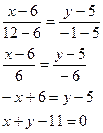
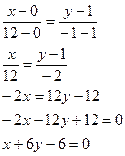
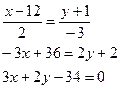
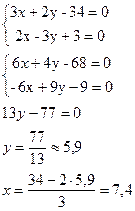
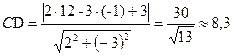
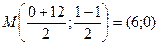 . Уравнение MN:
. Уравнение MN: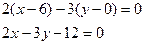
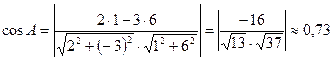
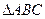 : А(1;4), В(-2; 3), С(3; -2). Найти:
: А(1;4), В(-2; 3), С(3; -2). Найти: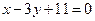 ВС:
ВС: 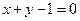 AC:
AC: 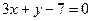
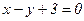 , ≈2,8 в)
, ≈2,8 в) 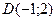 г)
г) 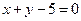 д)
д)