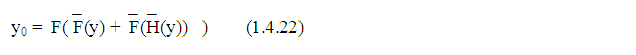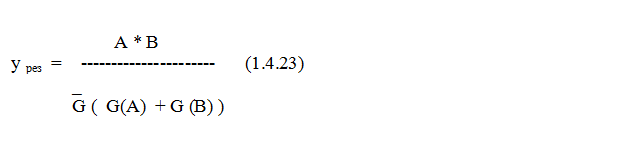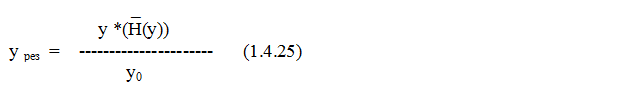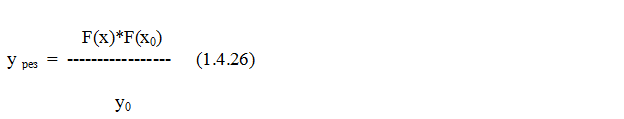Формула ОС для степенной функции. Оос.

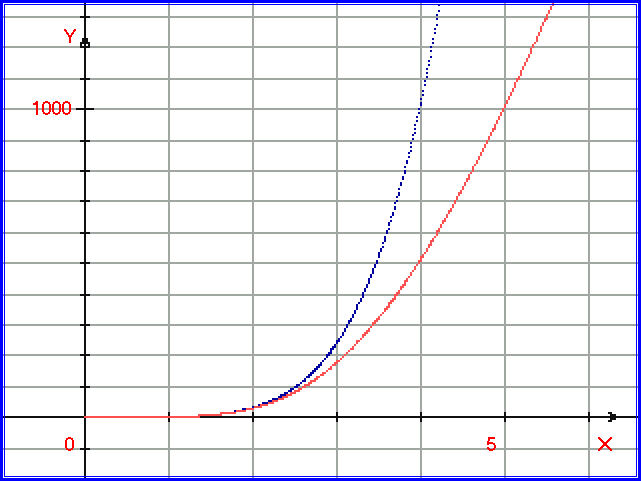
Рассмотрим степенную функцию при ООС. Найти решение для степенной функции аналитическим способом довольно сложно. Степенная функция:

y = xⁿ.

Обозначим её как y =Fs(x).

Рассмотрим степенную функцию, при ООС (согласно рисунку 1.4.9.):

y = Fs(s) = xⁿ - функция прямой передачи (блок 3),

p = - η*y - функция обратной передачи (ООС, блок 1), η=dy/y - коэффициент обратной связи, dy - количество выходного сигнала, подаваемого на входной сумматор,

s=x+p - функция сумматора (блок 2).

Тогда s = x - η *y, отсюда:

y = Fs (x - η *y) (1.4.13).

В результате получается уравнение (1.4.13), решаемое методом подбора решения на ЭВМ с помощью подпрограммы MidI_S01. Подпрограмма MidI_S01 разработана для одной входной переменной (в данном случае «x»). Как можно заметить, эта подпрограмма вычисляет результат ОС для функций («чёрных ящиков»). Функция, для которой ведётся поиск решения, должна быть монотонной, возрастающей. Подпрограммы, подобные MidI_S01, могут решать задачи для расчёта ООС и для более сложных функций прямой передачи («чёрных ящиков»).

001 procedure MidI_S01(x,n1,r1:real;var y:real);002 var003 Imax, Imin, x0, E: real;004 begin005 E:=0.00001;006 Imax:= power(x,n1);007 Imin:=0;008 repeat009 begin010  y:=(Imax+Imin)/2;011  x0:=power(y,1/n1) + r1*y;012  if x0 > x then Imax:=y else Imin:=y;013 end until (x0+E > x) and (x0-E < x);014 end;

В строке 6 подпрограммы функция y = xn обозначена как power(x,n1).

n1 – показатель степени, r1 – коэффициент обратной связи.

Строка 6 – это максимальное значение, от которого начинается поиск решения – это вход в цикл подпрограммы.

Строка 11 – это выражение, рассчитывающее x.

Приведём несколько примеров поиска решений ООС для нескольких степенных функций. На рис. 1.4.18 построим степенную функцию y = x⁵ синими точками, а поверх неё - функцию с ООС y = (x – 0,001*у)⁵ красными точками:

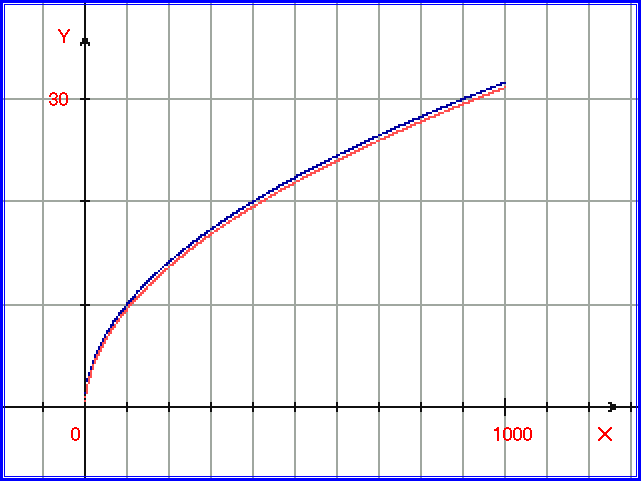
Рис. 1.4.18. Степенная функция y = x⁵ построена синими точками, поверх неё построена функция ООС y =(x – 0,001*у)⁵ красными точками.

На рис. 1.4.19. построим степенную функцию y = x^0.5 синими точками, а поверх неё – функцию ООС  y =(x – 0,99*у)^0.5 красными точками:

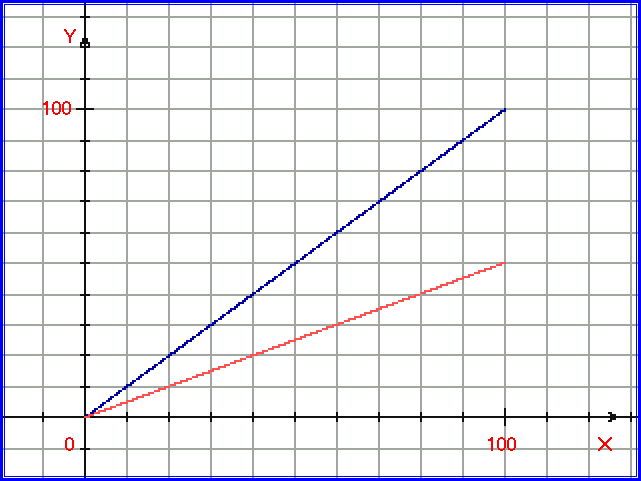
Рис. 1.4.19. Степенная функция y = x^0.5 построена синими точками, поверх неё построена функция ООС  y =(x – 0,99*у)^0.5 красными точками.

Линейная функция y = x¹ является частным случаем степенной функции. На рис. 1.4.20 построим степенную функцию y = x¹ синими точками, а поверх неё – функцию ООС  y =(x – 0,99*у)¹ красными точками:

Рис. 1.4.20. Степенная функция y = x¹ построена синими точками, поверх неё построена функция y =(x – 0,99*у)¹ красными точками.

Общий случай ОС.

Mатематическое определение ОС.

Дана функция y = F(x). Введем в неё обратную связь:

y = F(x, y) = F(u), где F(u) - неявная функция.

Это общее математическое определение функций с ОС. Рассмотрим общий случай ОС.

Обратная связь.

Рассмотрим для примера ООС. Выразим её как 2 функции (2 процесса):

x - аргумент сигнала, или прямой связи (прямой передачи),

x₀ – аргумент сигнала обратной связи (ОС, обратной передачи).

Рассмотрим схему:

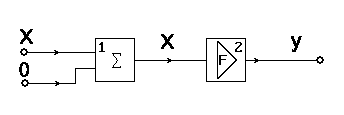
Рис. 1.4.21. Элементы-блоки функции прямой передачи.

В схеме на рис. 1.4.21 ОС отсутствует, здесь показана только функция прямой передачи:

у = F(x) = А (1.4.16),

где А – функция прямой передачи.

Рассмотрим схему, в которую дополнительно включены элементы функции обратной передачи (ОС):

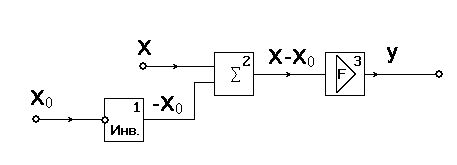
Рис. 1.4.22. Элементы-блоки функции обратной передачи.

Видно, что формула ОС здесь выражается как

y = F(x - x₀)    (1.4.17)

Из (1.4.17) найдём x:

Теперь вычислим y0 = F(x), подставив x из выражения (1.4.18):

Выражение (1.4.19) написано для условий, соответствующих как схеме с прямой связью, так и схеме с обратной связью, и для таких условий выделена специально переменная y_0, поскольку значение y₀ может отличаться от решения y в реальной системе с ОС. Осталось выразить y через аргумент ОС х₀ как сложную функцию (см. рис. 1.4.23):

у = H(F(x₀)) (1.4.20)

Отсюда найдём x₀:

Подставим (1.4.21) в (1.4.19):

Теперь положим в формуле перехода процессов (см. выше):

Внешняя функция у нас:

Сравнивая знаменатель (1.4.23) с выражением (1.4.23), мы видим, что в знаменателе мы получили y₀, поэтому:

Как видно из (1.4.22), y₀ учитывает как функцию прямой передачи, так и функцию обратной передачи – это было указано в (1.4.19), из-за чего это выражение и было обозначено не как y, а как y₀, то есть величина y₀ несколько парадоксальна и практического значения не имеет, но возможно, что она стремиться к y. Далее находим из выражений (1.4.25), (1.4.16) и (1.4.21):

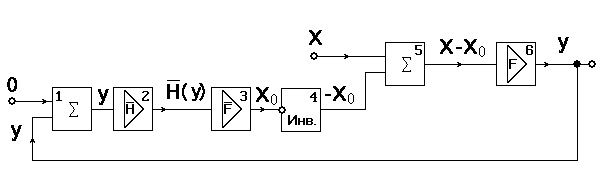
Выражение (1.4.26) представляет собой формулу перехода процессов, которая имеет в своём составе функцию прямой передачи и функцию обратной передачи -y0 сочетает элементы прямой передачи и элементы обратной передачи. Здесь не выведено решение для системы с ОС (для «чёрного ящика» такого вывода просто нет - решение находится методом подбора с помощью алгоритма). Здесь показана просто связь системы с ОС с некоторым переходом двух процессов.

Блок-схема нашей системы с ОС показана на рис. 1.4.23.:

Рис. 1.4.23. Блок-схема системы с ОС: блоки 1 и 5 – сумматоры, блоки 2, 3 и 6 – функциональные усилители, блок 4 – аналоговый инвертор. Блок 6 определяет функцию y = F(x), блоки 2 и 3 определяет функцию:

Математический смысл уравнения (1.4.26) таков: функции прямой передачи и обратной передачи равноправны и являются двумя функциями перехода процессов. Переход процессов имеет внешнюю функцию y =F(x).

1.4.5. Подробное рассмотрение процессового перехода на примерах.